Relationship between Gravitational field, irreversibility, Bohr’s Hydrogen Model and Schrödinger’s equation
The individual objects that make up our universe have an inevitable interaction with the environment, and no system can operate in a completely isolated environment in reality. Obviously, we cannot create an environment that can entirely eliminate the influence of gravitational field. We start our work from the irreversibility between light emission and detection inside a quantum well (QW) diode to investigate the origin of irreversibility. The light emission is an irreversible process to the light detection, and the MQW photodiode can only detect shorter-wavelength light emitted from the MQW diode with the identical MQW structures. On the basis of three postulations: (1) The individual objects cannot be completely isolated from the environment in reality, and the gravitational force must always act on them under any circumstances; (2) The objects at different positions have different quantized states in a gravitation field and their masses in turn depends on their energy states. (3) the amount of work done against the gravitational force is different when the object moves from one place to another and goes back to the starting position. We have made the crucial relationship between the gravitational field and the irreversibility, and arrived that gravitational effect creates the irreversibility. This suggests that we have to supply an additional energy against the gravitational force. As a result, only the closed loops occur on the equipotential surfaces, the line integral of force F around these loops in a gravitational field would be zero. Otherwise, the irreversible processes happen. Therefore, we would have

Therefore, we should consider the gravitational effect in Bohr’s hydrogen model, in which the gravitational force in association with other forces create a dynamic motion of the electron in the quantized equipotential surfaces. We can arrive the following conclusions:
1, The orbits are quantized equipotential surfaces, and the electron undergoes random reversible motion on the equipotential surface under the balanced force, which can be represented by a random wave function;
- Each equipotential surface exhibits a discrete distribution of quantized energy levels, and the transition between different energy levels will result in resonance absorption and emission phenomena;
- The shift of electron on different equipotential surfaces is irreversible with different light absorption and emission spectra. The electron in the ground state can only absorb shorter-wavelength (higher-energy) photons to move back to the excited state.
Furthermore, we connect these ideas with the quantum-mechanical equation. Considering the motion in the gravitational field, Schrödinger’s equation should be modified as:

Where![]() is the amplitude for an electron. For a stable state, we can get
is the amplitude for an electron. For a stable state, we can get
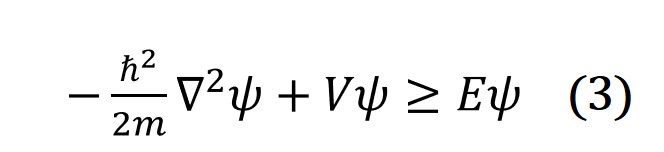
Moreover, because the objects at different positions have different quantized states in a gravitation field and their masses in turn depends on their energy states, therefore, m, the mass of the object, is related to its total internal energy E by m = E/c2, c is the velocity of light. Hence, Schrödinger’s equation may be further modified as:
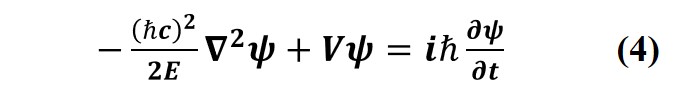
The laws of nature should be unified. There are no absolutely isolated systems. Only by considering the influence of cosmic gravity can we connect various natural phenomena and gain a deeper understanding of physics.


Please sign in or register for FREE
If you are a registered user on Research Communities by Springer Nature, please sign in