Neural and tensor networks are powerful computational tools that have a wide range of practical applications in physics, computer science and most fields of science. These act to bridge a specific problem to some computational representation for a person or computer to interact with. Their designs are often hierarchical, modular and exhibit repeating patterns. Within the field of machine learning the attempt to automate the design of neural network architectures, called Neural Architecture Search (NAS), has been successful in achieving state-of-the-art performance [1,2]. At the same time tensor networks have seen great success in computational physics and share many similarities with neural networks [3]. Since quantum circuits are a subclass of tensor networks, this overlap extends to them, making it  possible to apply techniques from NAS. With this in mind, we propose a framework for representing this class of tensor networks which enables search space design and architecture search. Using this representation, we employ a genetic algorithm to perform Quantum Phase Recognition (QPR) as an example of search. We also use the framework to justify the importance of circuit architecture in quantum machine learning by generating a family of Quantum Convolutional Neural Networks (QCNNs) and evaluate them on a music genre classification dataset, GTZAN. The framework is implemented as an open-source Python package enabling both person and computer to design these computational representations.

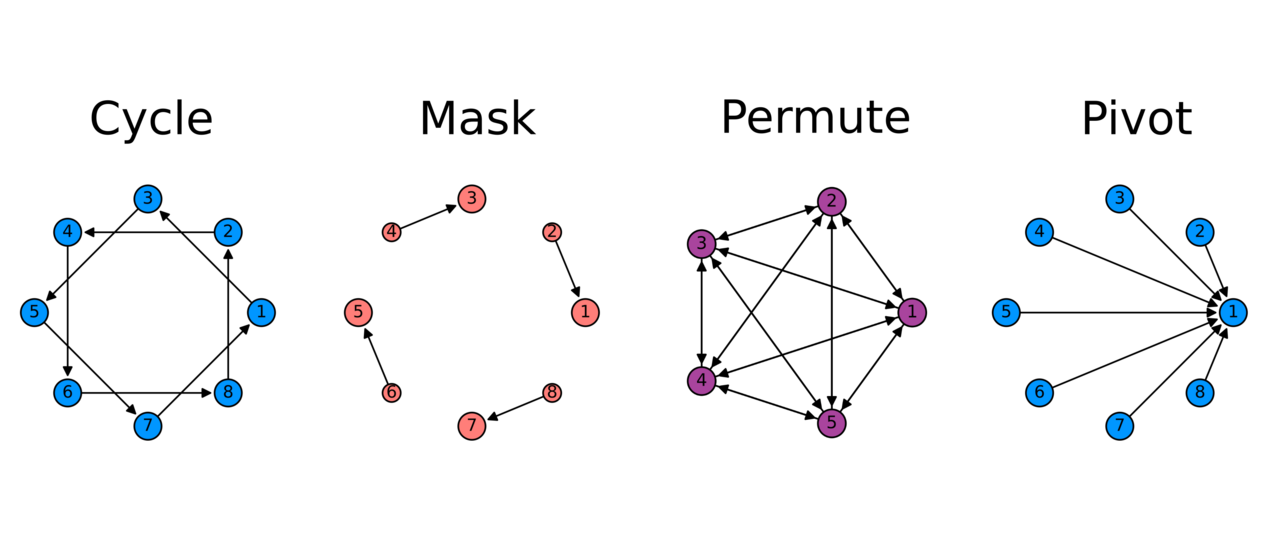
Hierarchical representation and NAS

NAS consist of three main categories: search space, search strategy and performance estimation strategy [4]. The search space defines the set of possible architectures that a search algorithm can consider, and carefully designed search spaces help improve search efficiency and reduce computational complexity [5]. Search space design often involves encoding architectures using a cell-based representation. Usually, a set of primitive operations, such as convolutions or pooling, are combined into a cell to capture some design motif (compute graph). Different cells are then stacked to form a complete architecture. Cell-based representations are popular because they can capture repeated motifs and modular design patterns, which are often seen in successful hand-crafted architectures.

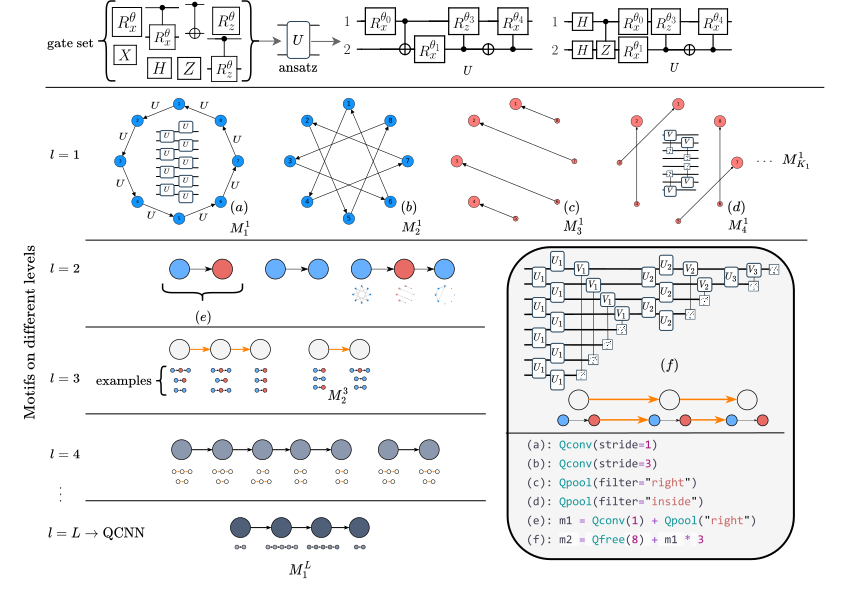
One problem with the cell-based representation for NAS is that the macro architecture, the sequence of cells, is fixed and must be chosen [4]. Recently, Liu et al. [5] proposed a hierarchical representation as a solution, where a cell sequence acts as the third level of a multi-level hierarchy. In this representation, lower-level motifs act as building blocks for higher-level ones, allowing both macro and micro architecture to be learned. In this work, we  follow a similar approach and represent a quantum circuit architecture as a hierarchy of directed graphs. On the lowest level are primitive operations such as convolutions and pooling. The second level consists of sequences of these primitives, such as convolution-pooling or convolution-convolution units. Higher-level motifs then contain sequences of these lower-level motifs. For example, the third level could contain a sequence of three convolution-pooling units, as seen in Figure 1f.

Quantum Phase Recognition

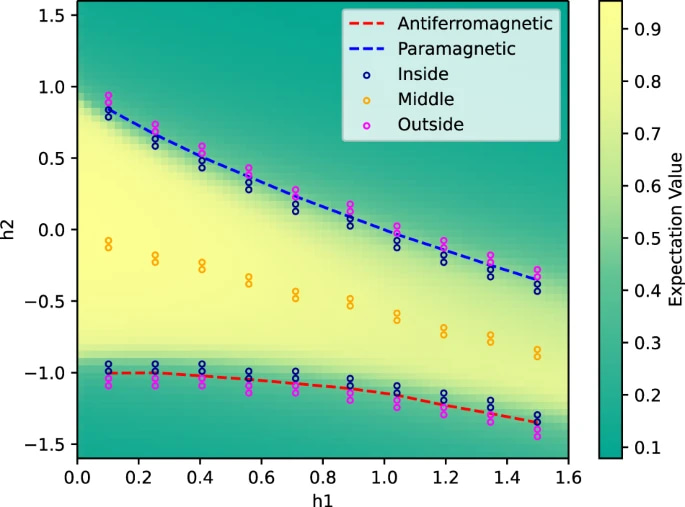
We applied  our architectural representation in conjunction with evolutionary search to perform QPR.  The objective was to recognize a ℤ2×ℤ2 symmetry-protected topological (SPT) phase for a ground state that belongs to a family of cluster-Ising Hamiltonians. For the evolutionary algorithm,  mutations involve replacing a primitive within a motif with a randomly generated one. Crossover works by combining two motifs end-to-end, if possible, or interweaving them otherwise.  To facilitate comparison, we considered the same task and setup from the original QCNN paper [6]. The evolutionary algorithm managed to find a circuit with a reduced number of parameters, from 1309 to 11, and an improved  sample complexity just inside the phase boundary, 36 against 61. The expectation values of the circuit are shown in Figure 2.

Representing quantum algorithms:

While the space of possible architectures is very large, many algorithms have implicit symmetries baked into them. The framework is designed to capture these symmetries explicitly so that they can be used as tools by an algorithm. For example, the n-qubit Quantum Fourier Transform is created with the following code [7]:

qft = (
    Qpivot(mapping=Qunitary("h()^0"))
    + Qpivot(
        mapping=Qunitary("cp(x)^01"),
        share_weights=False,
        symbol_fn=lambda x, ns, ne: np.pi * 2 ** (-ne),
    )
    + Qmask("1*")
) * n
qft_n = Qinit(n) + qft

This demonstrates that its design can be captured using only pivots and masks. Designing compute graphs in this manner allows for a compact yet expressive representation of the computation. For instance, the GIF below illustrates how tensor tree network circuits can be generated with just a few lines of code. Examples of Grover's search and MERA-like circuits are also showcased on the package page  [7].

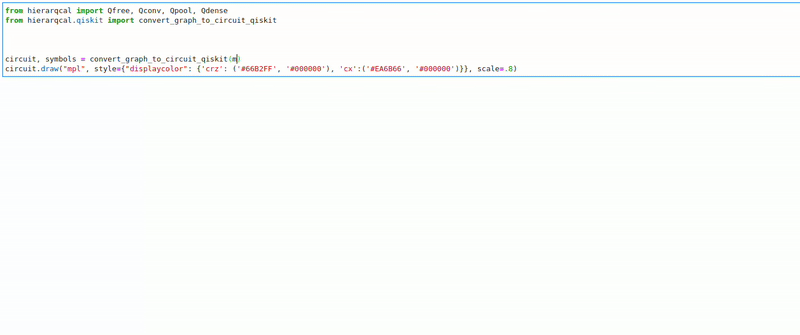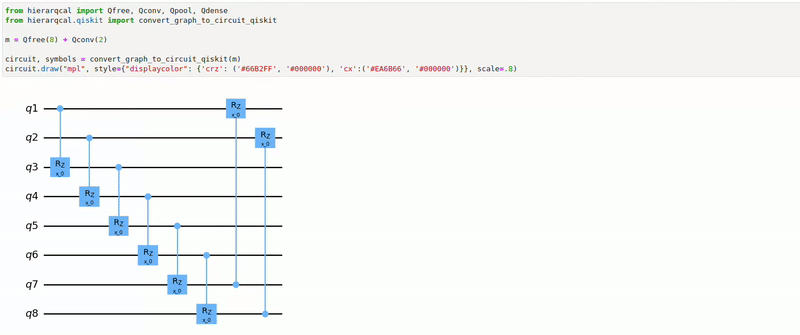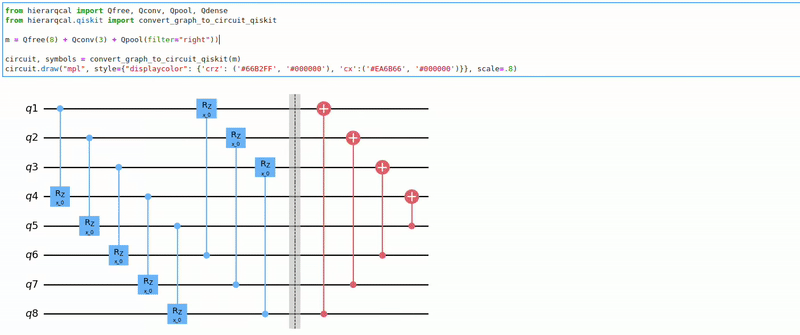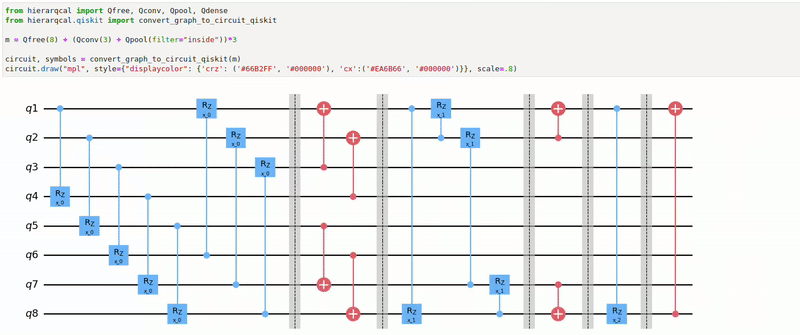
References

1. Zoph, B. & Le, Q. V. Neural architecture search with reinforcement learning. Int. Conf. Learn. Represent. https://openreview.net/forum?id=r1Ue8Hcxg (2017).
2. Real, E., Aggarwal, A., Huang, Y. & Le, Q. V. Regularized evolution for image classifier architecture search. Proc. AAAI Conf. Artif. Intell. 33, 4780–4789 (2019).
3. Grant, E. et al. Hierarchical quantum classifiers. NPJ Quantum Inf. 4, 65 (2018).
4. Elsken, T., Metzen, J. H. & Hutter, F. Neural architecture search: a survey. J. Mach. Learn. Res. 20, 1–21 (2019).
5. Liu, H., Simonyan, K., Vinyals, O., Fernando, C. & Kavukcuoglu, K. Hierarchical representations for efficient architecture search. Int. Conf. Learn. Represent. https://openreview.net/forum?id=BJQRKzbA- (2018).
6. Cong, I., Choi, S. & Lukin, M. D. Quantum convolutional neural networks. Nat. Phys. 15, 1273–1278 (2019).
7. Python package relating to this work