In condensed matter physics, Majorana zero modes are exotic quasiparticle excitations, named after the Italian physicist Ettore Majorana, which possess unique properties that make them potential building blocks for topological quantum computing. For instance, exchanging the position of Majorana zero modes is not commutative, in the sense that the final outcome depends on the order in which the exchanges are performed. Moreover, Majorana zero modes are “topologically protected”, that is, robust against disorder and other perturbations, due to their intrinsic topological nature. In other words, a Majorana mode cannot be destroyed by a local perturbation without changing the global topological makeup of the whole physical system. Intense research is devoted to exploiting these properties to build a topological quantum gate, which hopefully will become the fundamental building block of a so-called “topological” quantum computer.

Theoretically, Majorana zero modes can be realized in two different platforms: 1) At the vortex cores of a two-dimensional (2D) unconventional (spin-triplet) topological superconductor; 1) At the edges of a one-dimensional (1D) topological superconductor realized, for instance, by a semiconducting nanowire in proximity to a conventional superconductor, or atomic chains deposited on a superconductor in an external magnetic field. But what if there was an alternative and more flexible way to create and manipulate these modes? 

In our study, we propose a novel platform where Majorana zero modes are localized at the ends of 1D “stripes” within a 2D topological insulator in proximity to a conventional superconductor. These stripes, which we call “topologically nontrivial stripes”, are induced by the inhomogeneous nature of the superconducting order parameter in the presence of a finite magnetic field parallel to the surface. The key idea is that the variation of the phase of the superconducting order parameter across the 2D platform creates regions where the system behaves effectively as a 1D system. In these regions, the topological invariant—which is a quantity that determines whether a system is in a topological phase—alternates between trivial and nontrivial values, depending on the phase of the order parameter. As a result, the Majorana zero modes localize at the ends of these quasi-1D regions, offering a new way to generate and manipulate them. This approach, which relies on the embedding of quasi-1D quantum states in a 2D platform, is conceptually different from the previously mentioned proposals based on 1D and 2D homogeneous superconductors.

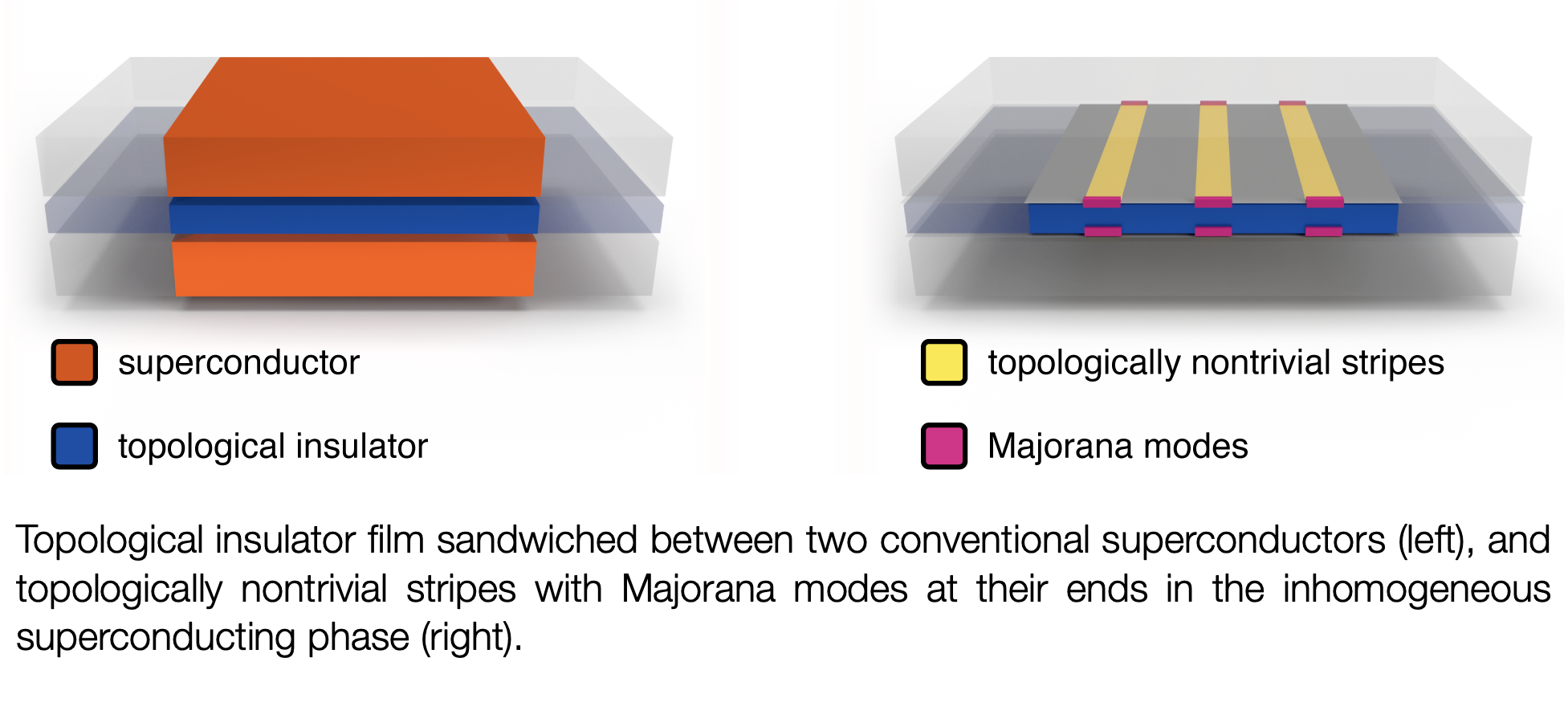
A new route to topological quantum computation

The manipulation of Majorana zero modes for quantum computing hinges on the ability to braid them—an operation where two Majorana zero modes are exchanged in a specific way that alters the quantum state of the system. In 1D setups, such as nanowires or atomic chains, Majorana zero modes are confined to the ends of the 1D system. Topologically nontrivial stripes can be thought of as "movable" 1D wires embedded within a 2D platform. By controlling the in-plane magnetic field, it is possible to move and rotate these stripes, thereby moving the Majorana zero modes with them. This capability allows the manipulation of the quantum information within a topological quantum gate. Furthermore, by using external gates, it is possible to fuse or split the stripes, thereby “fusing” Majorana zero modes, which is a crucial operation for reading the quantum information embedded in the quantum gate. In essence, the ability to create, move, fuse, and manipulate topologically nontrivial stripes within a 2D platform potentially paves the way for more practical and scalable quantum computing devices.

Nonlocality

Another exciting aspect of this new platform is the potential to create highly nonlocal Majorana zero modes. In certain regimes, the Majorana zero modes that localize at the ends of the topologically nontrivial stripes can hybridize into a single quantum state that is spread across spatially separated points. This state maintains exactly zero energy, even at finite system sizes, making it a robust candidate for quantum computing applications. What makes these nonlocal states particularly intriguing is their connection to quantum-mechanical supersymmetry (SUSY). In high-energy physics, SUSY is a symmetry that relates bosons and fermions, extending the Standard Model by adding a sibling to every known elementary particle. In the platform we proposed, the nonlocal Majorana zero modes exhibit emergent SUSY, adding an additional layer of exotic physics which opens up new possibilities for exploring fundamental questions in theoretical physics.

Exploring exotic quantum phenomena

The potentialities of topologically nontrivial stripes extend beyond the creation of Majorana zero modes. By coupling several topologically nontrivial stripes to a metallic bath can lead to the realization of Yang-Lee anyons with non-unitary and nonabelian statistics. Moreover, by coupling the stripes to a disordered quantum dot may effectively realize the Sachdev-Ye-Kitaev model, which reproduces the maximally chaotic dynamics of black holes, and may reveal unexpected connections between condensed matter physics and black hole dynamics. This could lead to experimental tests of theories that until now have been purely theoretical, potentially leading to new insights into the nature of quantum chaos and gravity.

Experimental platforms

In our work, we mainly focus on creating topologically nontrivial stripes in a platform obtained by sandwiching a topological insulator thin film between two conventional superconductors. However, topologically nontrivial stripes may also be created in other systems, employing inhomogeneous superconducting orders in strontium ruthenate, iron pnictides, organic superconductors, two-dimensional electron gases, and two-component cold atomic Fermi gases with population imbalance and effective spin-orbit coupling. Finally, the experimental detection of Majorana zero modes at the ends of topologically nontrivial stripes would also provide indirect evidence of inhomogeneous superconductivity.

Conclusion

In conclusion, our study proposes a novel approach to create and manipulate Majorana zero modes by exploiting inhomogeneous superconductivity in topological insulators/superconductor 2D structures. This potentially offers greater flexibility for realizing novel blueprints for topological quantum gates and the potential to explore a wide range of exotic quantum phenomena such as supersymmetry, quantum chaos, and analog quantum gravity.