The existence of quantum entanglement is one of the primary feature of quantum physics which  is lacking in classical physics. In the quest for deeper understanding of the relation between the long-range quantum entanglement with the phases of quantum matter, scientists have taken a big step forward  quantifying quantum entanglement through the tool of quantum entanglement entropy. von-Neumann entropy is the most commonly used quantum entanglement entropy, however calculating it requires the knowledge of wave function which makes it a forbidden task in quantum Monte Carlo simulations. In this context, Renyi entanglement entropy which is the generalization of von-Neumann entropy, proves to be obtainable in quantum Monte Carlo simulations due to its special trace structure. This trace structure allows scientists to rewrite Renyi entanglement entropy into the form of the ratio of two partition functions which can be naturally cast into the Monte Carlo simulation cells. 

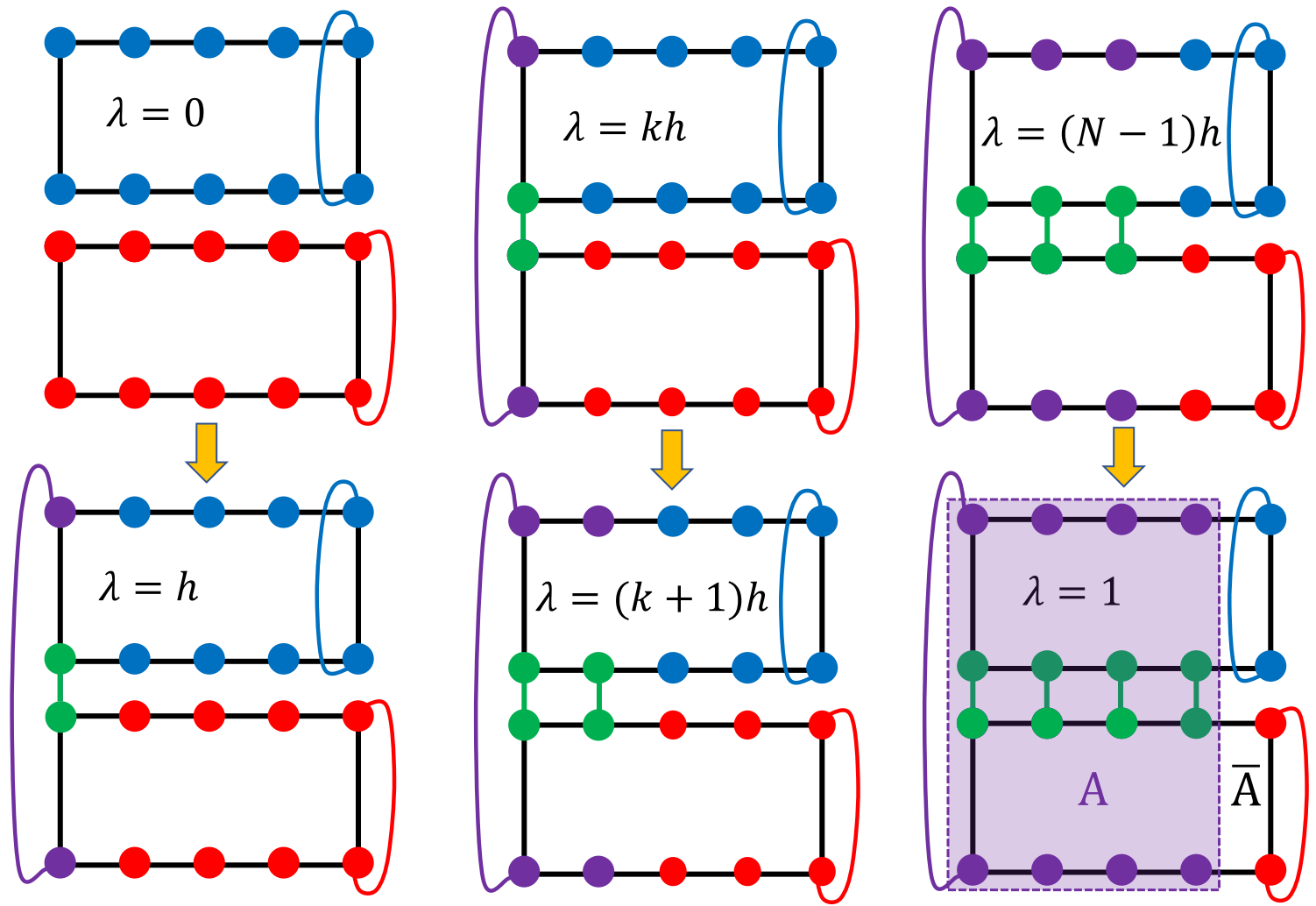
Great success has been made in the measurement of entanglement entropy during the past decades. However, these measurements are heavily limited to either low dimensions or small system sizes, making it hard to analyze the scaling behaviour of the entanglement entropy. Our work is based on the newly developed nonequilibrium method and we make a fundamental improvement by splitting the nonequilibrium process into many small pieces and making the whole process parallellable in Monte Carlo simulations.  The schematic plot of our algorithm is illustrated in Fig 1.

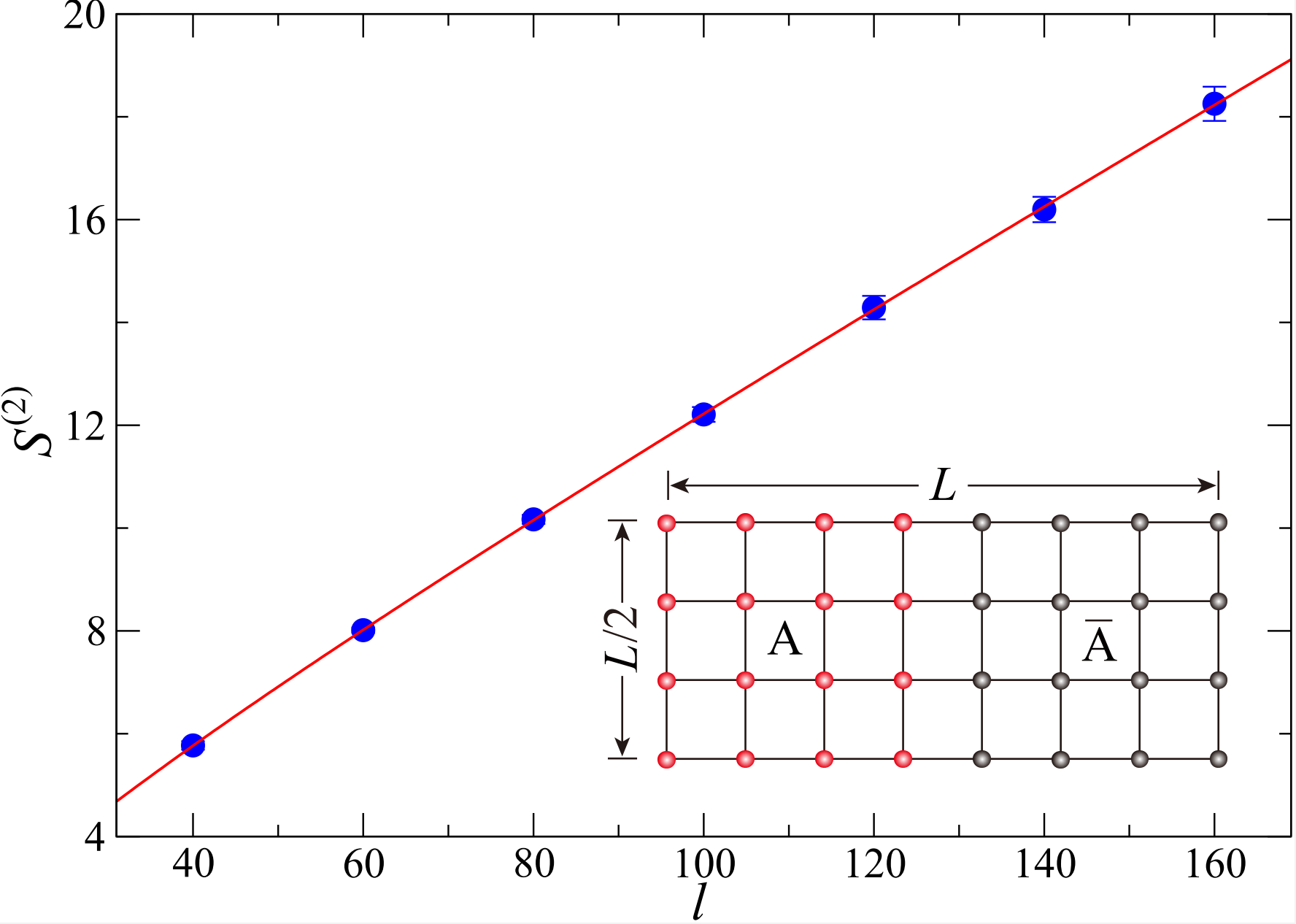
We test this new method on three representative models in quantum many-body physics.  The first one is the two dimensional antiferromagnetic Heisenberg model. At zero temperature, this model breaks the SU(2) spin rotation symmetry, which contributes a logrithmic correction to the entanglement entropy besides an area law term with the length of the entanglement boundary, and the coefficient of the correction is one half of the total number of Goldstone modes in the symmetry breaking phase.  As shown in Fig 2, we measure the second Renyi entropy in the spontaneously symmetry breaking phase and find the subleading coefficient is 1 which is exactly one half of the number of Goldstone modes N=2 in this phase.  

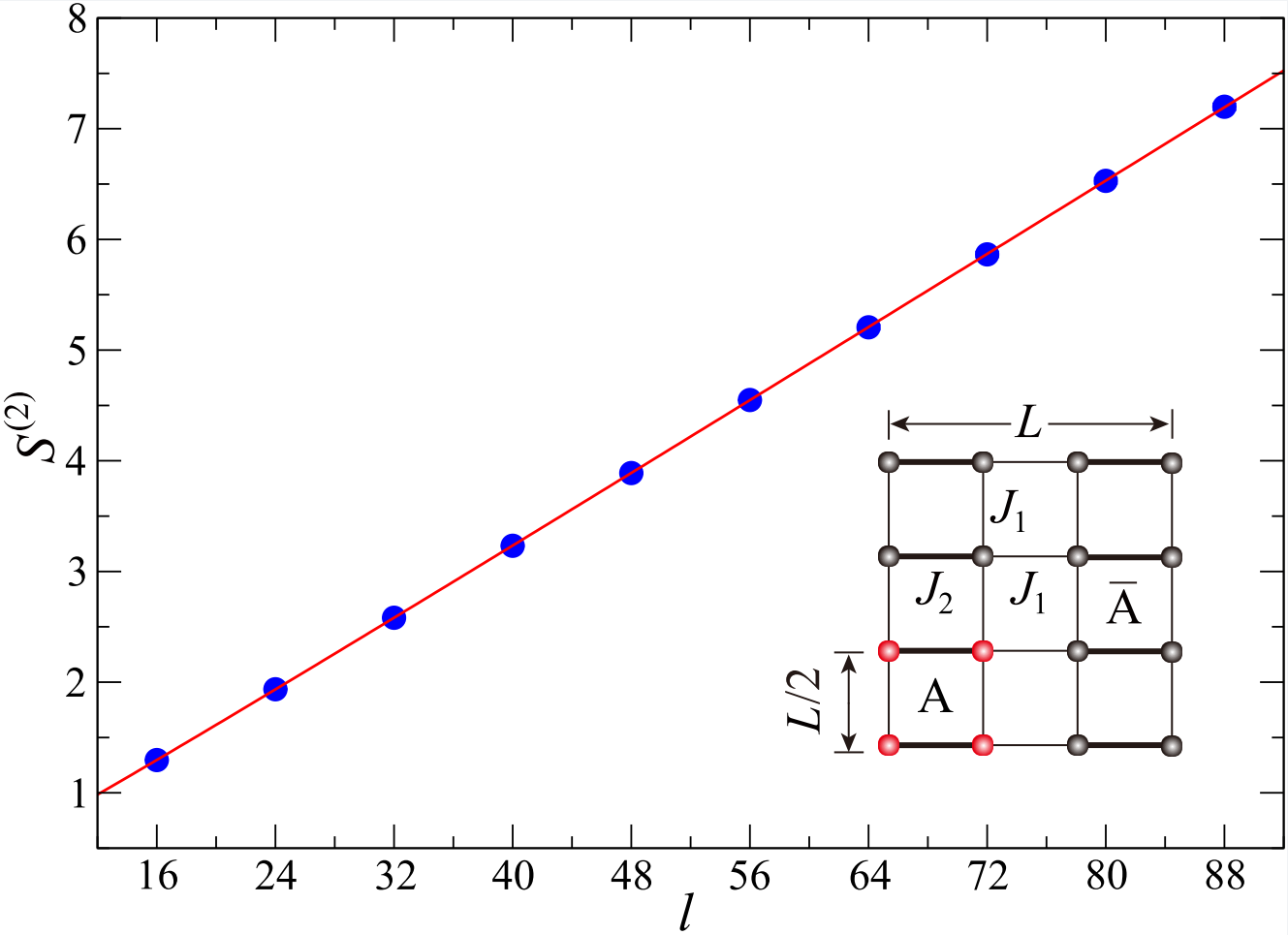
We then measure the Renyi entanglement entropy at the O(3) critical point of the J1-J2 model. The O(3) critical point is described by conformal field theory (CFT) and if the entanglement boundary is not smooth it will give a logrithmic correction to the entanglement entropy. As shown in Fig 3, we choose  A to be a square region so that there will be four 90-degree corners on the boundary, which give approximately an addition of 0.072-0.085 to the logrithmic coefficient . Because there is no spontaneous breaking of any continuous symmetry here, the logrithmic corrections only owe to the corner effect. Using our algorithm, the Renyi entanglement entropy at this critical point is precisely obtained and the fitting results gives the value of  the logrithmic coefficient to be 0.081(4), which satisfies very well with the expected value. 

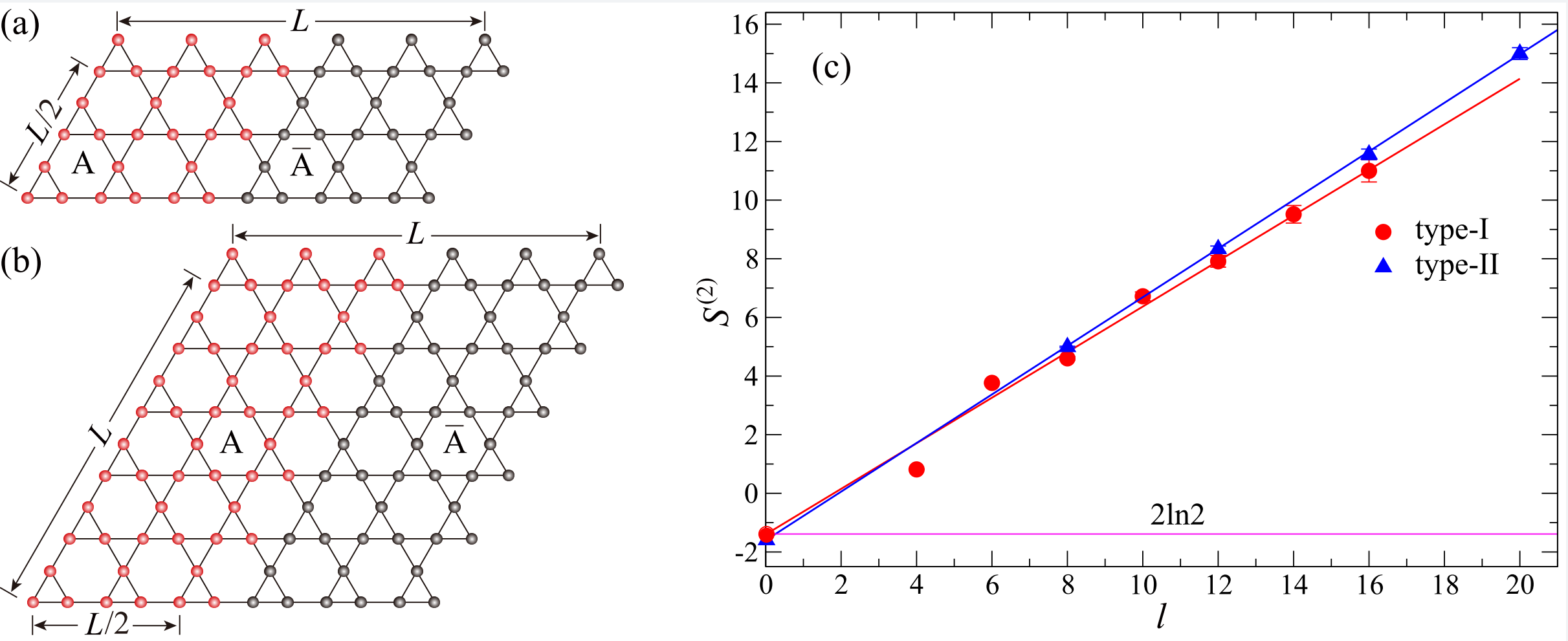
Finally, we turn to a difficult yet interesting case, the Z₂ quantum spin liquid, which has topological order and no conventional order parameters. Besides an area law term with the length of the entanglement boundary, there is a  constant called topological entanglement entropy which characterizes the total quantum dimension of the phase and equals twice of the logrithimic of the quantum dimension on a torus geometry. As illustrated in Fig 4, we carry out the measurement on the kagome lattice Balents-Fisher-Girvin model which hosts the Z₂ topological order on a smooth boundary. Because there are no spontaneous symmetry breaking and sharp corners, the intercept of a straight line will give us the topological entanglement entropy. Our results on two different lattices show that the intercept is 1.4(2) which agrees well with the theoretical prediction of 2ln(2). 

The above three examples show the power of our nonequilibrium increment method. Our new algorithm makes the measurement of entanglement entropy in quantum many-body systems an easier task!

Authors:

Dr. Zheng Yan and Dr. Bin-Bin Chen are postdocs in the physics department of The University of Hong Kong (HKU), and Mr. Jiarui Zhao is a PhD candidate in the same department.