We live in a complicated world that consists of various complex subsystems, like the financial system, climate system, and ecological system, to name a few. Hopefully, we all want to understand the future behaviors of the complex systems around us, and then guide decision-making. However, it is challenging and sometimes unavailable to directly find the rules and achieve ahead predictions in many real-world complex systems. Fortunately, various datasets of components in complex systems are accessible, in particular, time series data, collected from temporal evolutions of real-world observations, are considered to contain rich information of complex systems, e.g., species population series are used to estimate the stability of ecosystems, and temperature series are useful indicators in climate systems. Finding the future behaviors of systems components can be helpful for the predictions of complex systems. To understand this, we consider the classic Lorenz system that consists of variables , and (Figure 1(a)). Each component outputs a time series (Figure 1(b)) as the Lorenz system evolves in state space. If we can predict the future behaviors of all these variables (Figure 1(c)), it is likely to estimate the future behaviors of the Lorenz system (Figure 1(d)).

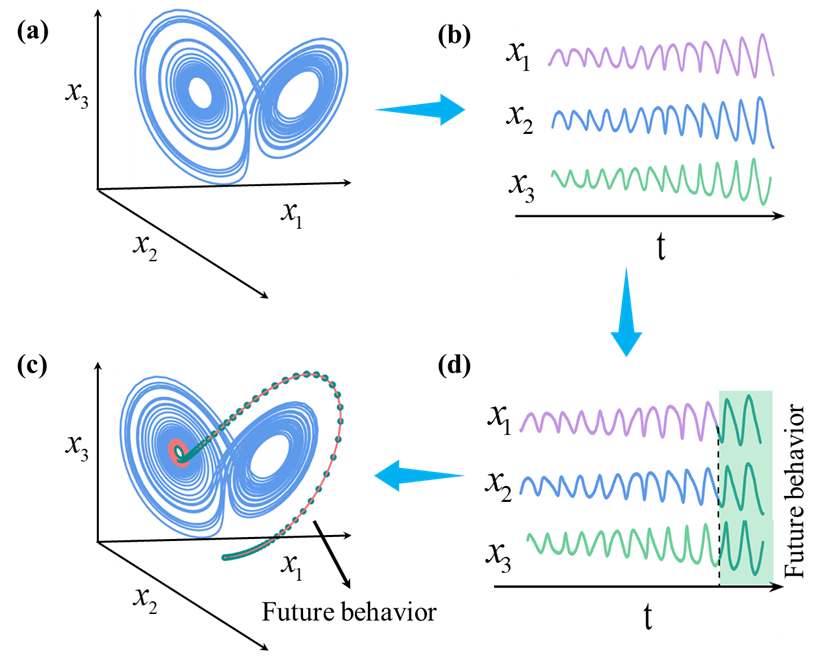
               Figure 1. Complex system and its output time series.

        As discussed above, it is possible to predict the future behaviors of complex systems through their output time series. However, it is still an open issue, possibly due to three reasons, i) Real-world systems often consist of many interconnected units, e.g., multiple spatiotemporal observations in climate systems and thousands of functionally connected neurons in the brain, they therefore output a large number of time series variables, known as high dimension. It is challenging to create a method that can forecast all observations in a complex system. Some works, as an approximation, forecast some representative variables from systems. However, identifying such representative variables remains a challenging task. Moreover, one should be cautious to ignore those ‘unimportant variables’, in which small perturbations may be amplified and propagated to all components, resulting in heavy changes in system behaviors (known as cascading effects). Instead, the capacity to predict the future states of all components can help to better estimate the future behavior of a complex system. ii) It is challenging to find a generalized predictor when forecasting all observations. For a target variable, the predictors are often selected empirically, e.g., several target-related observations. If regarding all the remaining variables as predictors, some redundant information may negatively affect the performance (e.g., noise and irrelevant variables to the target variable, especially for high-dimensional real-world systems. iii) It is challenging to find a generalized method to forecast all observations. For each target, some approaches may train different models (e.g., the predictive models for  and  are completely independent). There may need N models for an N-dimensional system, leading to a high computational cost.

        To overcome the aforementioned obstacles, we develop a data-driven predictive framework by a combination of feature embedding (manifold learning) and delay embedding. Our framework yields reliable predictions for all components via a generalized and practical predictor, i.e., the system’s low-dimensional representation from manifold learning. The theoretical foundation of our framework is based on the ground truth that high-dimensional systems often contain redundant information and that their essential dynamics or structures can be characterized by low-dimensional representations, e.g., the meaningful structure of a 4096-dimensional image (64 pixels by 64 pixels) can be characterized in a three-dimensional manifold with two pose variables and an azimuthal lighting angle. These low-dimensional representations can be sufficiently identified from two powerful techniques: feature embedding and delay embedding. To understand this, we consider the 3-dimensional Lorenz system and the 3-dimensional Rössler system, they show quite different structures in state space (Figure 2(a) and (d). From delay embedding, we can find their 2-dimensional representations, which show similar topological structures with original systems (Figure 2(b) and (e)). From manifold learning, we can also find their low-dimensional representations (Figure 2 (c) and (f)). Notice that all the information on low-dimensional representation from feature embedding can be obtained, while some elements are unknown on the low-dimensional representation from delay embedding. Since low-dimensional representations (in different coordinates) from the two approaches show isomorphic structures with the original system. This enables us to find the unknown elements on the representations from delay embedding by one-to-one mapping between two low-dimensional representations. Additionally, in a dynamical system, each time series variable can reconstruct a low-dimensional representation via delay embedding. Therefore, the low-dimensional representation from feature embedding can be practically selected as a generalized predictor to potentially identify the future dynamics of all components in complex systems. The substantial potential of our framework is shown for both representative models and real-world data involving Indian monsoon, electroencephalogram (EEG) signals, foreign exchange market, and traffic speed in Los Angeles Country. Our framework overcomes the curse of dimensionality and finds a generalized predictor, and thus has potential for applications in many other real-world systems.

                        Figure 2. Low-dimensional representation of complex system.

        However, our framework fails to predict different components synchronously. In other words, for each target variable, one needs to train a suitable mapping. Additionally, our framework also has limitations for situations in which a system experiences abrupt, rapid, and even irreversible transitions (known as tipping points). The behavior of a system shifts between contrasting states, and the historical rules may not be held when a system crosses the threshold, leading to poor predictions of our framework.