Probabilistic computing using diffusive memristors
Published in Electrical & Electronic Engineering

With the rapid development of big data, dealing with the exploding amount of data is one of the major technological challenges. Hence, the need for designing a computing scheme to solve complex tasks, which cannot be efficiently executed with classical computing based on the von Neumann architecture, is growing. Quantum computing showed the potential to outperform the classical ones, but maintaining cryogenic operating temperature leads to enormous energy consumption. Resolving the challenges mentioned above, probabilistic computing (p-computing) built using the stochastic nature of CuxTe1-x/HfO2/Pt (CTHP) memristors capable of performing logic gates with invertible mode, showing the expandability to complex logic operations, is proposed. Unlike bits (classical computing) and qubits (quantum computing), probabilistic bits (p-bits), which are used in p-computing, have probabilities of being ‘0’ and ‘1’. The p-bit fluctuates between ‘0’ and ‘1’, and an input variable controls the probability.
The p-computing network is an energy-based network that updates the network to minimize the total energy. Its operation principle stems from the theoretical background of quantum annealing, which carries similar features to a stochastic Hopfield network. Figure 1a is the Hopfield network, where Χi is the neuron output with values of either 0 or 1, ωij is the fixed weight value connecting the two neurons, and θi is the applied bias. The output is updated to minimize the energy function of the system for a given input, and the direction of the update is determined by the partial derivative of the energy by Χi. The inputs and outputs of the p-computing network follow that of the Hopfield network, as shown in Figure 1b. However, in the case of p-computing, the synaptic connection (Sij) can be extended to the connection weight between 3 or more p-bits, depending on the applications.
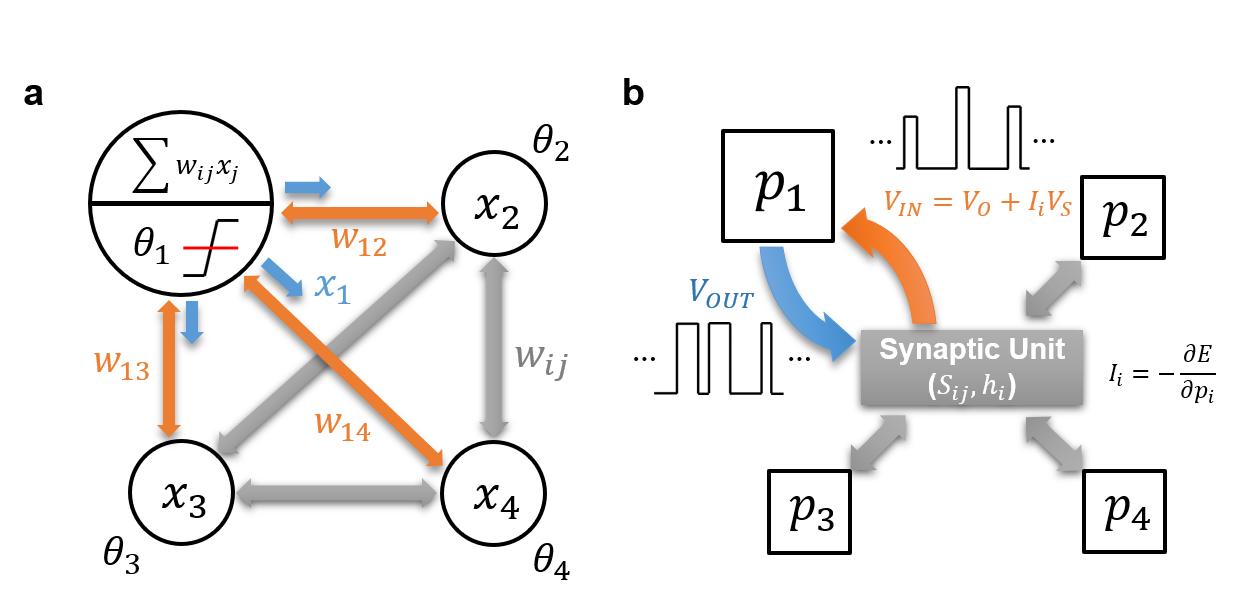
Figure 2a is a two-terminal memristor-based p-bit with a simple circuit design utilizing the stochasticity of threshold switching behavior in the CTHP memristor. The sigmoidal fitting curve shows the critical property of the p-bit that the input voltage can control the probability of device switching (or p-bit state). A three-p-bit network based on the memristor-based p-bits is required to perform an AND logic operation, as shown in Figure 2b. Figure 2c is the hardware p-computing network that consists of memristors, a field programable gate array (FPGA), and a digital-to-analog converter (DAC). The memristor-based p-bits are connected to the inputs of FPGA, and the FPGA outputs three new p-bits from the given logic operations based on the inputs and cost functions. The AND operation is shown in Figure 2d. The unique feature of p-computing is that the answer is found probabilistically, not fixed into a deterministic result. The most probable output, the output with the minimum energy function, is chosen as the answer. Unlike machine learning, which takes several training epochs to optimize the weight matrix, the p-computing outputs the results in one-shot without training the weights. Another strong point of this network is the invertible calculation that can be performed using the same hardware. This way, all 16 Boolean logic operations can be implemented in both forward and inverted directions.

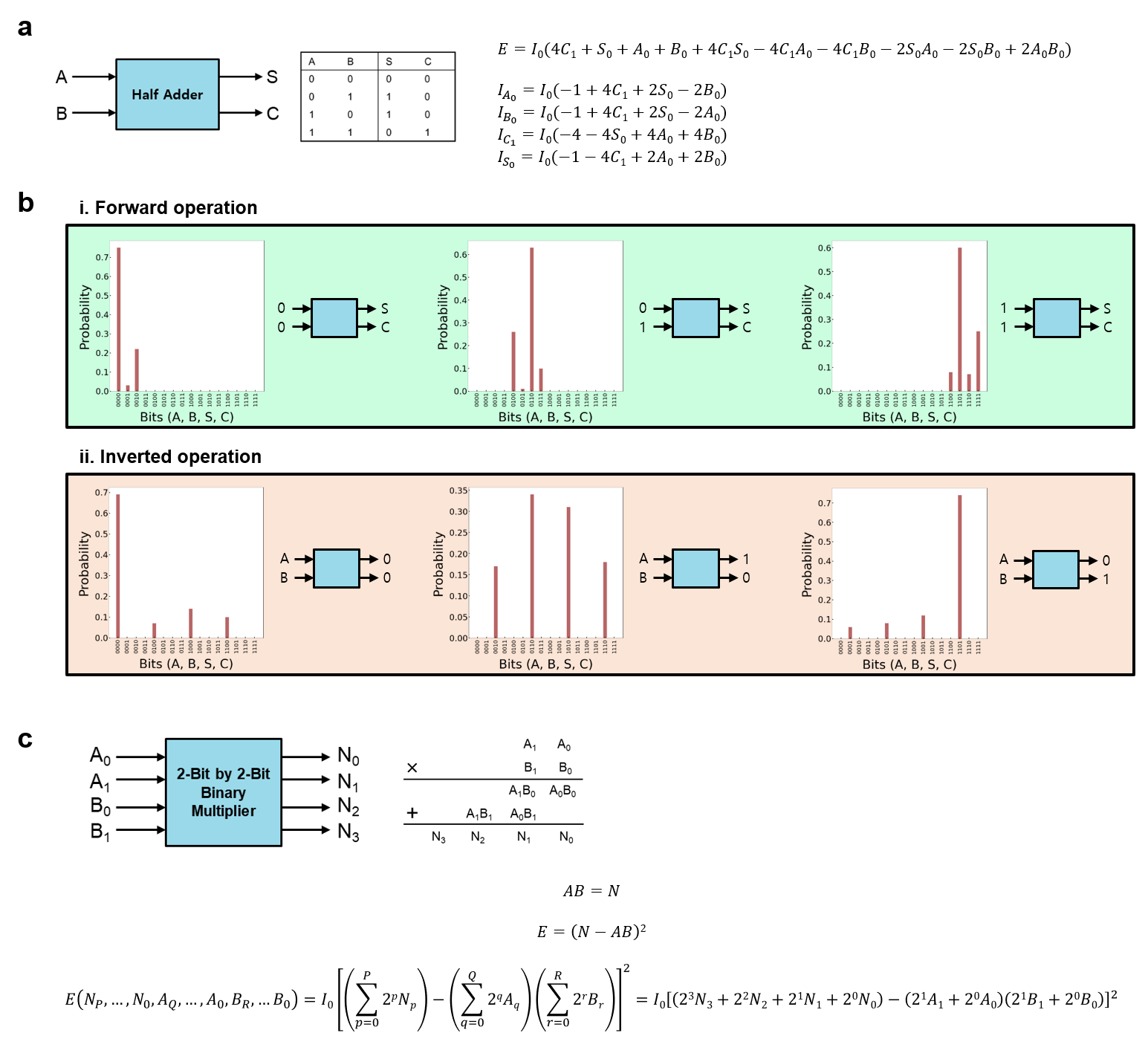
Memristor-based p-computing can function as an arithmetic logic unit, and a 1-bit half-adder can be operated in a four-p-bit network, as shown in Figure 3a. Using four p-bits, each for two inputs, sum and carry, both forward and inverted operations are performed in Figure 3b. A full adder is also possible by simply adding a p-bit that represents a bit carried in from the previous operation. By exploiting the unique property of memristor-based p-bits, Figure 3c suggests more complex operations, such as multiplication and factorization, which are invertible. For highly complex logic operations, the number of involved memristors should be increased accordingly. Any calculation is possible in a one-shot method with a suitable cost function for a particular operation.
The memristor-based p-computing demonstration expanded the possibility of adopting the memristor in computing applications. It paves the way towards a next-generation computing scheme with the potential to overcome the memory wall issue of the current von Neumann computing method.
For more details, please refer the full article with the link: https://doi.org/10.1038/s41467-022-33455-x
Follow the Topic
-
Nature Communications

An open access, multidisciplinary journal dedicated to publishing high-quality research in all areas of the biological, health, physical, chemical and Earth sciences.
Related Collections
With Collections, you can get published faster and increase your visibility.
Women's Health
Publishing Model: Hybrid
Deadline: Ongoing
Advances in neurodegenerative diseases
Publishing Model: Hybrid
Deadline: Mar 24, 2026


Please sign in or register for FREE
If you are a registered user on Research Communities by Springer Nature, please sign in