Quantifying Cell-State Densities in Single-Cell Phenotypic Landscapes Using Mellon
Published in Bioengineering & Biotechnology, Cell & Molecular Biology, and Mathematics
Our fascination with cell-differentiation, has driven us to investigate its intricacies through the lens of single-cell data. The journey began with my mentor, Manu Setty, who has been exploring the subtle state changes in stem cells since 2014, right when single-cell data began to shine light on this complex process. The challenge was clear: to develop computational tools that could effectively combine data from numerous cells and provide meaningful insights.
Manu’s earlier work on tools like Palantir embraced the continuity of cell differentiation, leveraging diffusion maps, cell-fate probabilities, and the phenotypic manifold. These efforts laid the groundwork for what would become Mellon, our approach to representing cell states continuously.
My path intersected with Manu’s when I was deep into my PhD, tackling gene-expression deconvolution in tumor tissues. The complexity of distinguishing gene-expression patterns in tumor cells and infiltrating immune cells made it clear that mere gene expression signatures were insufficient to represent cell types and tissues. The need for multivariate distributions to represent cell types became evident.
Joining Manu’s lab at Fred Hutchinson Cancer Center in 2021 marked the beginning of our collaboration. We were united by the goal of applying a rigorous, mathematically principled approach to deciphering single-cell data from differentiating tissues. Hematopoiesis became our first target, prompting us to ponder how static data could reveal dynamic cell-differentiation processes.
The realization that we needed a comprehensive representation of cell states—one that captured cell abundance along trajectories—led us to the concept of cell-state density. The high dimensionality of the cell-state space posed a significant challenge, but we found our solution in the phenotypic manifold. While cell states require many dimensions for accurate description, their trajectories and variabilities follow a lower-dimensional structure. This insight guided us toward using the nearest neighbor distribution to quantify cell-state density.
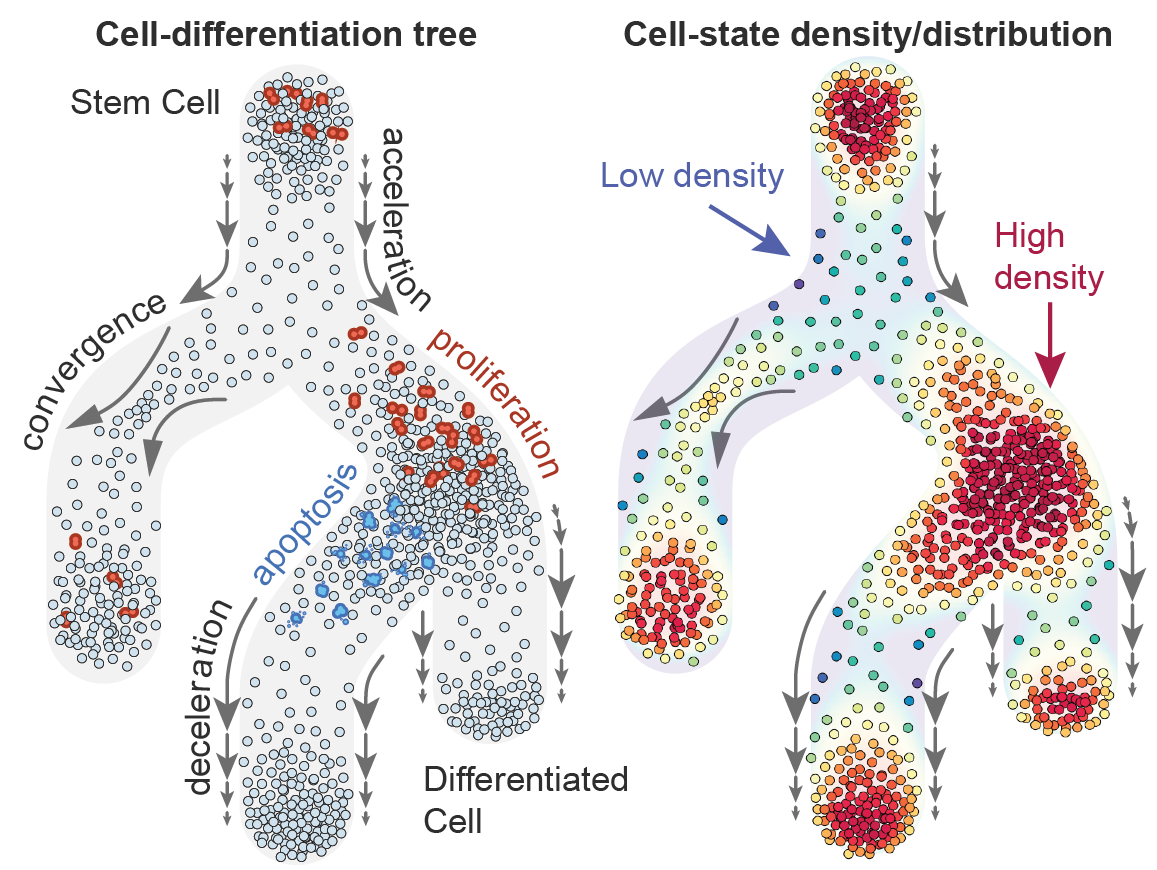
Inspired by the Poisson distribution, we established a probabilistic connection between density and the nearest neighbor distribution. Additionally, Gaussian Processes came to our rescue, addressing the challenge of combining observations from multiple cells and producing a differentiable density function. Despite the initial slow implementation with PyMC3, the insights we gained were astounding. We saw high-density spots and low-density transitions, revealing clear traces of differentiation dynamics in our data.
Motivated by these insights, we aimed to optimize our implementation, leveraging the XLA compiler and sparse Gaussian Processes for scalability to datasets with millions of cells. This led to the development of Mellon.
With Mellon, we realized that a cell-state density function could offer a holistic representation of cell types and tissues. Using such a representation could theoretically allow to sample from the distribution reproducing the original measured single-cell states. Further, the density function can converge, meaning it becomes stable as more data is gathered, providing a complete picture of the tissue.
We are excited about the potential of Mellon and its applications in the scientific community. We look forward to exploring new directions and building on this innovative approach to single-cell data analysis.
For a detailed look at our findings, please read our paper published in Nature Methods: https://www.nature.com/articles/s41592-024-02302-w.
We would like to extend our heartfelt thanks to our co-authors Cailin Jordan, Brennan Dury, Christine Dien, and especially my mentor, Manu Setty, whose guidance has been invaluable.
For those interested in exploring Mellon further, the code is available on GitHub: https://github.com/settylab/Mellon.
We can’t wait to see where Mellon will take us and what exciting applications it will inspire!
Follow the Topic
-
Nature Methods

This journal is a forum for the publication of novel methods and significant improvements to tried-and-tested basic research techniques in the life sciences.
Related Collections
With Collections, you can get published faster and increase your visibility.
Methods development in Cryo-ET and in situ structural determination
Publishing Model: Hybrid
Deadline: Jul 28, 2026


Please sign in or register for FREE
If you are a registered user on Research Communities by Springer Nature, please sign in