Rolling stones and structural stability of LK-99

Explore the Research

On the dynamical stability of copper-doped lead apatite - npj Computational Materials
npj Computational Materials - On the dynamical stability of copper-doped lead apatite
In July 2023, the world was astonished by a groundbreaking claim of room-temperature superconductivity in a copper-doped lead apatite compound dubbed LK-99. The claim was supported by the observation of magnetic (half-)levitation and a sudden drop in resistivity, interpreted as demonstrating the Meissner effect and zero resistivity state characteristic of superconductivity. However, the claim has been disputed by numerous subsequent experimental studies that provided alternative explanations rooted in ferromagnetism and the presence of Cu2S impurities rather than superconductivity.
Despite an apparent consensus having now been reached on the experimental side, the original claim also prompted numerous theoretical works. Copper-doped lead apatite is a complex material, and its description is a challenging test for the capabilities of modern theories and computational tools. In this context, theoretical models have provided a range of controversial predictions, from flat electron bands to thermodynamic barriers to copper doping. But perhaps the most surprising theoretical prediction is that both the parent lead apatite and the copper-doped lead apatite (LK-99) compounds are dynamically unstable. What this means is that the structures that have been reported experimentally for the parent compound for over 70 years have now been predicted to be impossible structures. And similarly the recently measured structure of the copper-doped variant is also predicted to be an impossible structure. When we first read about these claims we were extremely puzzled, particularly those regarding the parent compound, which had been well-characterized for decades. Did this indicate severe limitations in the models used? Or did this reveal the true nature of the compounds that had been missed experimentally?
The dynamical stability of a material can be tested by "pushing" the constituent atoms away from their equilibrium positions. If the atoms go back to their initial positions after the push, then we say the material is dynamically stable. This is analogous to pushing a stone uphill from the bottom of a valley, and the stone rolling back to the equilibrium point at the bottom (left panel in Fig. 1). If the atoms do not go back to the initial position after the push, then we say that the structure is dynamically unstable, and the system instead adopts a new different structure. This is analogous to pushing a stone downhill from the top of a mountain, to which the stone will not get back and instead roll down towards a different point (right panel in Fig. 1).
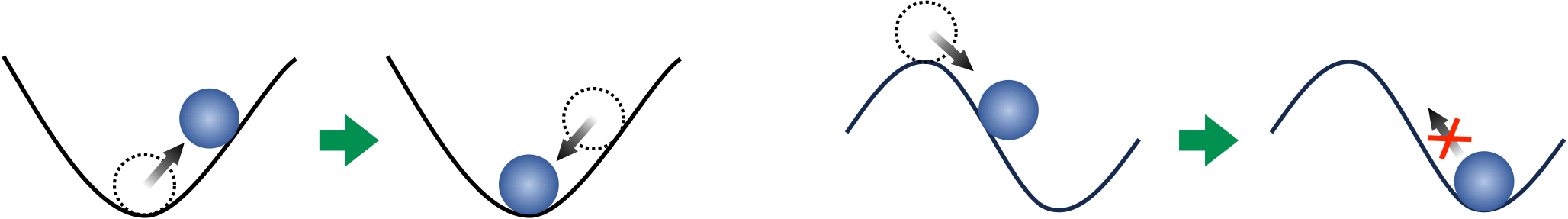
Technically, the dynamical stability of a compound can be determined through phonons, the quantum mechanical version of atomic vibrations. If phonons have "real" frequencies, the structure is dynamically stable; if phonons have "imaginary" frequencies, the structure is dynamically unstable. However, calculating phonons themselves can be tricky. The standard approach, known as the harmonic approximation, relies on very small "pushes" to the atoms. While this method works well for many compounds, it can only determine dynamical stability at the absolute zero of temperature. Interestingly, the stability of some materials changes with temperature. To establish the dynamical stability of materials at high temperature, it is necessary to go beyond the simple model of the harmonic approximation, and instead consider anharmonic terms. Both harmonic and anharmonic calculations are computationally demanding, and their cost grows with the complexity of the material studied. Lead apatite and LK-99 are exceptionally complex compounds, testing the limits of applicability of these methods.
In our work, we used recently developed state-of-the-art computational methods to study both harmonic and anharmonic phonons. The key result of our work is the demonstration that, once these state-of-the-art methods are used, both parent lead apatite and copper-doped lead apatite compounds are dynamically stable at room temperature (see atomic structures in Fig.2). The parent compounds are largely stable at the harmonic level. This contrasts with earlier reports that predicted dynamical instability, and the reason we could obtain better results is due to recent algorithmic developments that allow us to reduce the computational cost of harmonic calculations and test a larger number of directions in which to push the atoms to assess their stability. To put numbers into this, we could perform these extensive tests simulating lead apatite with only 132 atoms, whereas similar calculations with older methods would have required over 3000 atoms, a computationally prohibitive task. For LK-99, our calculations reveal that it is unstable at the harmonic level, consistent with earlier reports, but our more sophisticated anharmonic model then shows that the material stabilizes at room temperature. Interestingly, the harmonic instability of LK-99 suggests the possible existence of a temperature-driven phase transition to a structure with lower symmetry at lower temperatures (right panel in Fig. 2), and we hope to stimulate future experimental and theoretical work to clarify this hypothesis.
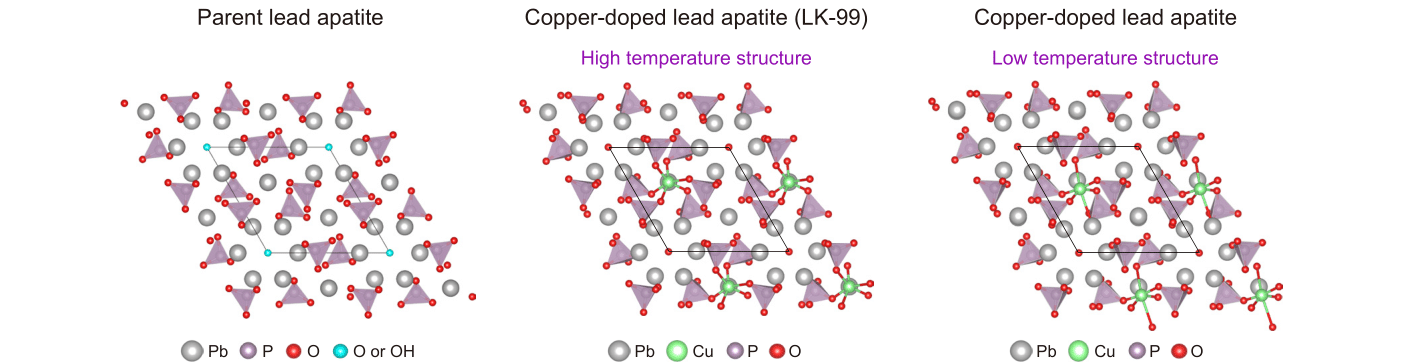
Our results resolve a puzzling suggestion by multiple earlier computational works that claimed that the experimentally reported structures of both parent and copper-doped lead apatite compounds were impossible structures. Instead, we find that with state-of-the-art theories, these structures exist, in full agreement with the current experimental understanding of lead apatite. This provides a sound foundation on which to explore the controversial superconductivity claims of LK-99.
More generally, we believe that lead apatite is a nice example to illustrate the ability of state-of-the-art first principles methods to fully characterise a complex and experimentally relevant system. However, our work also demonstrates that reliable results and conclusions for structural stability can only be reached with a careful consideration of the physical models and algorithms used.
You can read more about this work in our article in npj Computational Materials following the link: https://doi.org/10.1038/s41524-024-01206-9
Follow the Topic
-
npj Computational Materials

This journal publishes high-quality research papers that apply computational approaches for the design of new materials, and for enhancing our understanding of existing ones.
Related Collections
With Collections, you can get published faster and increase your visibility.
Recent Advances in Active Matter
Publishing Model: Open Access
Deadline: Sep 01, 2026
Computational Catalysis
Publishing Model: Open Access
Deadline: Dec 31, 2025





Please sign in or register for FREE
If you are a registered user on Research Communities by Springer Nature, please sign in