Different materials behave differently when light shines on them. Think about it: a mirror bounces back almost all the light, a window glass lets most light pass through, and a black shirt soaks up almost all the light. When light is beamed onto materials that don’t conduct electricity easily (called semiconductors), something amazing happens. Some of the electrons of the material absorb light’s energy and become excited, leaving behind a vacant space, or "hole". This electron-hole pair, called an exciton, moves together, carrying energy.  

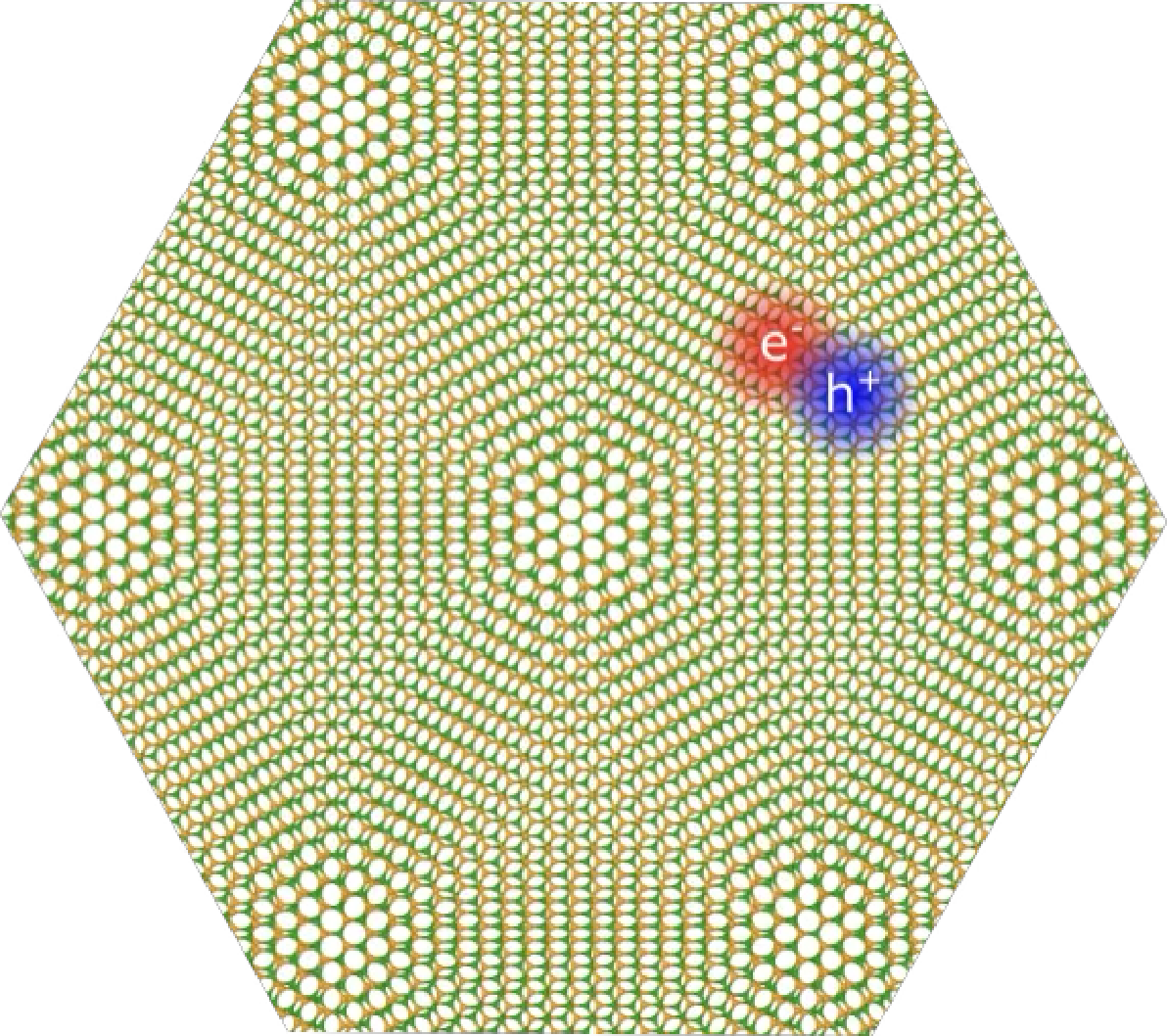
To create efficient solar cells and light-emitting diodes, we need to understand and control excitons in materials. For example, solar cells convert sunlight into electricity by generating electron-hole pairs and then separating them to produce electricity. The efficiency of a solar cell depends critically on how tightly these electron-hole pairs are bound, how far they can travel, and how long they live before losing their energy. But there's a challenge: predicting how excitons behave is limited to simple systems, even with modern supercomputers. These computations take weeks to months to complete, making it hard to truly design materials with target applications. To overcome this challenge, we developed a new computational approach based on first-principles (i.e., no knowledge of lab experiments). Using this strategy, we successfully captured the behavior of excitons in moiré materials (see image). 

What is a moiré material?

Imagine taking two transparent sheets with regular grid patterns, placing one on top of the other, and rotating the top sheet while keeping the bottom one fixed. A beautiful moiré pattern emerges. Since 2018, scientists have been creating such patterns at the atomic scale using incredibly thin materials, such as graphene, which is a million times thinner than a human hair. These moiré materials (see image) have remarkable properties, including superconductivity - the ability to conduct electricity without resistance. What's even more exciting is that we can adjust these properties by changing the twist angle between the materials. This discovery has generated huge excitement among physicists, materials scientists, and chemists.  

 What's the challenge in computing excitons? 

Simulating excitons is a tough challenge, even for simple materials. The problem lies in solving a complex mathematical equation, known as the Bethe-Salpeter-Equation, which demands enormous computational power and time. To put this into perspective, using current methods, simulating excitons in a slightly twisted moiré material would take more than a thousand years - an astonishing amount of time.  

How did we overcome this challenge? 

We identified two major roadblocks in traditional methods for solving the Bethe-Salpeter-Equation: calculating complex electron-hole interactions and accounting for how materials respond to light-induced electron excitement (or "screening"). To overcome these challenges, we developed a new approach using localized functions and a simplified screening model, all computed from first-principles. This strategy greatly accelerated our computations. We applied this method to the well-known semiconductor moiré material WS₂/WSe₂, successfully capturing pioneering experimental results.  

What’s next? 

Our approach isn't just limited to moiré materials - it can be applied to other complex systems where traditional methods struggle, such as defects in solids and disordered materials. Looking forward, we envision scientists designing materials to create tailored excitonic states for specific applications, from ultra-bright light emitters to solar cells.