Suppressing the Chance to Cheat in Online Exams
Published in Neuroscience

Because of COVID-19, online learning transitioned into an important and necessary part of education. This includes online exams, but in a new form, where students complete an online exam at home, physically isolated but digitally well connected.
Cheating behaviors are everywhere, and not surprisingly in exams. There are many kinds of cheating tricks but collusion is much more popular than other types of cheating behaviors in online exams. Prior research indicates that collusion occurred in four fifths of cheating events. Clearly, social distancing is not a barrier to collusion, given the fact that almost every family has a number of computers and mobile phones. In this context, our distanced online testing (DOT) technology (Optimized collusion prevention for online exams during social distancing) was developed to eliminate collusion. The website for the current platform is http://www.distancedot.ml/

Figure 1. Online exams in the pandemic are challenging for examiners to supervise, when students answer questions at home with Internet / telecommunication tools readily available (Cartoon by Hannah Wang with permission).
It may appear impossible to avoid collusion when students are so conveniently connected across digital networks. However, with prior knowledge of students’ competence scores and via discrete numerical optimization, we can effectively suppress the collusion gain to an insignificant degree. Our proposed optimization method is complicated but the essence of the idea is easily explained as follows. Suppose that we have three groups of students in a class, corresponding to their competence levels at the top, average and bottom of the class. Further suppose that those who are in the same group perform very similarly so that there is no significant cheating gain within each group. As an example, let these students take an online exam consisting of 4 questions out of a pool of 6 questions. Then, different sequences of 4 questions from the pool are assigned to these groups in a manner that dictates every student must finish each question in a synchronized time slot, and outside the assigned time slot the students cannot modify their answers retrospectively. Heuristically, we can assign 4 questions to the three groups of students via circular shifting, yielding no cheating gain at all in this ideal scenario. Even if we do not have prior information about the students’ competence levels, we can still use a discrete optimization method for design of an online exam with a minimized cheating gain. The beauty of this approach is that despite the feasibility of students being able to communicate freely, they cannot gain much via collusion.
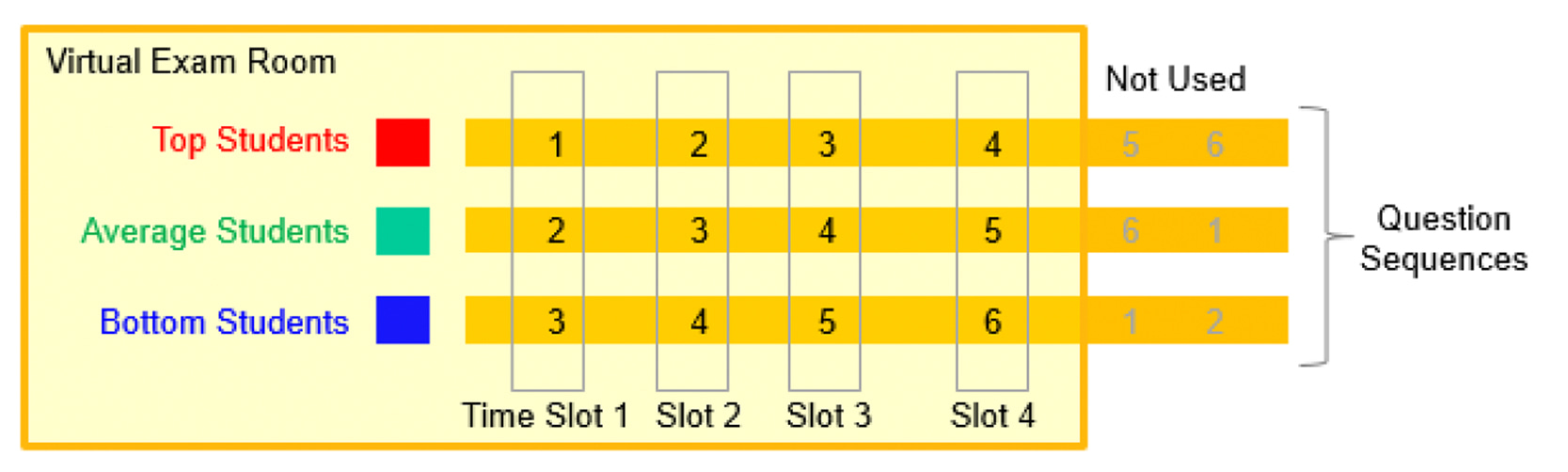
Figure 2. Our idea for minimization of collusion gains. In this online exam consisting of 4 questions from a pool of 6 questions, the grouped students provides permanent answers to each question within the corresponding time slot of the synchronized four slots.
As described in our paper, Optimized collusion prevention for online exams during social distancing, we have successfully trialled online exams using the DOT technology together with other complimentary methods include webcam, microphone, and academic integrity review. The overall feedback we received was very positive from students attending the Department of Biomedical Engineering, Rensselaer Polytechnic Institute (Troy, New York, USA). When students with cheating potential know that collusion is not feasible, their motivation to study the class materials is strengthened. In addition, their instructors can accurately assess the teaching outcomes and determine where improvements can be made. This constructive feedback loop created by the DOT technology has advanced the status of online education during the pandemic, and beyond. We believe that high-quality online courses will make a significant contribution to the future of education, and help democratize it globally.
Follow the Topic
-
npj Science of Learning

An online open access peer-reviewed journal dedicated to research on all aspects of learning and memory – from the genetic, cellular and molecular basis, to understanding how children and adults learn through experience and formal educational practices.
Your space to connect: The Psychedelics Hub
A new Communities’ space to connect, collaborate, and explore research on Psychotherapy, Clinical Psychology, and Neuroscience!
Continue reading announcementRelated Collections
With Collections, you can get published faster and increase your visibility.
Reimagining Teaching and Learning in the Age of Generative AI Agents
Publishing Model: Open Access
Deadline: Jul 13, 2026
Effects of lifestyle behaviours on learning and neuroplasticity
Publishing Model: Open Access
Deadline: Jun 09, 2026

Please sign in or register for FREE
If you are a registered user on Research Communities by Springer Nature, please sign in