The Spandrels of Ecological Architecture
Published in Ecology & Evolution

The paper in Nature Ecology & Evolution can be found here: http://go.nature.com/2jL5JNz
Networks have been present within ecological thinking since Darwin’s vision of the natural world as an “entangled bank”. The great British naturalist already envisaged the fabric of nature as a complex web of interacting species that would have been changing along the vast scales of evolutionary time. Such a systems-view of ecology and evolution has been a major thread in this scientific field, from classical studies of complexity versus stability to the recent advances in our understanding of microbiomes. Darwin’s views were a first step towards a more integrative approach beyond the specific life histories of particular species. In general terms, little can be said about the adaptation of organisms to changing environments without considering the network context. Specifically, when dealing with coevolution, the other species need to be included in the whole picture, since they are also part of the environment.

FIGURE 1: spandrels in architecture. Above, the ceiling of Bath Abbey in the U.K. Spandrels are the darker, profusely decorated structures in the middle of four rounded arches. Owing to their complex design, they can be interpreted perceived as functional key components of the system. Although this might be partially true, they are primarily a byproduct of other structural motifs. Photo by Ricard Solé.
Ecological networks had been studied previously by a reduced number of scholars, including among others Joel Cohen and Stuart Pimm. But with the rise of network theory, novel mathematical and conceptual approximations have paved the way for a renewed interest in the complexity of living structures under a systems-level view. With new tools used on existing data on pairwise interactions and improved sampling efforts, it was possible to delineate the first cartographies of ecological graphs. The emergent picture was a powerful one: ecological graphs display a number of universal properties, with common patterns shared by a myriad of ecological systems. One of them was the presence of small-world organisation i. e. the capacity to jump from one species to another by following a small number of links on the web. Another was heterogeneity, where the number of links displayed by a given species can vary widely: most species have a small number of interaction partners while a few can have many. Some networks display modularity: some species are more connected to those in a given subset (a module) than to the rest of the ecosystem. Finally, ecological networks are nested. Both generalists and specialist species in a nested system tend to interact with generalists whereas specialist-to-specialist interactions are rare. Nestedness informs of the presence of rich-clubs in ecosystems.
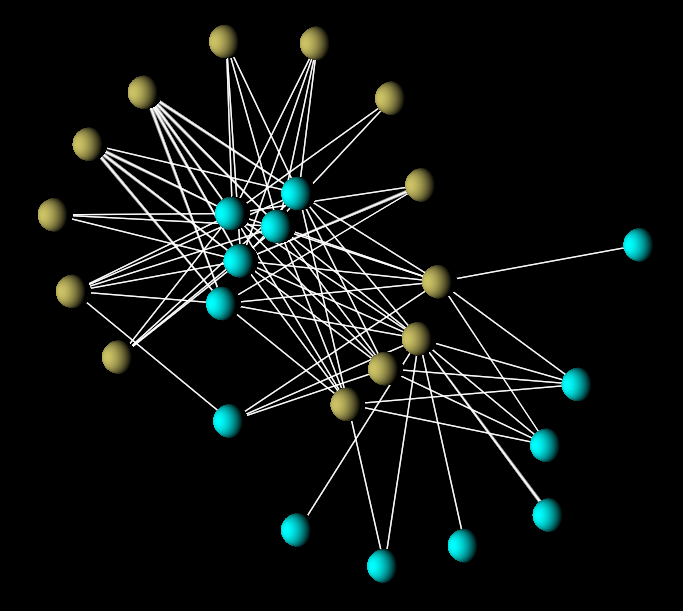
FIGURE 2: Pollinator network of Malpighiaceae oil-flowers and associated oil-collecting bees from a Brazillian steppe. Mutualistic interactions like these are very specialized and consistent with universal patterns of nested organisation. Data from Bezerra et al. (2009).
What is the origin of these patterns? A class of ecological webs known as mutualistic networks has extensively been explored over the last decade. Collections of pairs of plants and pollinators connected via a mutualistic interaction are examples of this class of systems. It has been suggested that nested webs provide a set of advantages in relation to the maintenance of biodiversity. The fact that the observed patterns are non-random, coupled to the benefits of the structural motifs could suggest a causal relationship: evolution might have favoured them. Under this considerations, the origins of the web organisation would be found in a systems-level selection of interactions. Similar arguments have been formulated within the context of cellular networks, where small world structure, heterogeneity, nestedness and modularity are common. Here too a few genes involved in regulation appear highly connected (they are hubs in the network) while most other genes just have a handful of interaction partners. This heterogeneous distribution of connections is known to have deep consequences on the response to perturbations and failures. Random mutations affecting genes having few links rarely have an impact. Instead, when changes affect hubs the consequences can be devastating. Not surprisingly, mutations in highly connected genes lead to proliferative diseases such as cancer. The fact that the regulatory network is heterogeneous could support the idea that heterogeneity has been favoured by evolution in an adaptive way.
Such an argument permeates evolutionary thinking, but it can be misleading. Some years ago some of us explored alternative scenarios of network evolution lacking any kind of selective advantage to see if they could explain the observed patterns. In particular, we investigated the role played by tinkering as a major force of evolutionary change. As suggested in a landmark 1976 paper by François Jacob, evolutionary change makes extensive use of reuse because, as opposed to an engineer, there is no goal or intentional design in the biological world. Novelties arise from generative rules such as gene duplication. This can be understood at the network level by introducing copy-paste mechanisms followed by changes in the redundant connections. What kind of networks systems emerge from such internal generative processes? Using simple graphs where nodes are chosen and duplicated randomly, with further random rewiring, most architectural patterns displayed by cellular networks can be explained by such growth processes. Since these models do not include any kind of function, selection is not invoked. As a consequence, pattern formation does not follow a function. Selection is only playing an indirect role.
These views are in accord with early ideas put forward by Steven J. Gould and Richard Lewontin in 1979. They proposed that some structural patterns displayed by biological systems might lack any adaptive meaning, being instead a byproduct of their inevitable constraints. The authors denominated these patterns “spandrels”. The word spandrel derives from architecture and refers to the spaces between two arches or between an arch and a rectangular enclosure (Figure 1). In evolutionary biology, a spandrel is a phenotypic characteristic that evolved as a side effect of a true adaptation. Assessing the balance between contingency and adaptation in evolution has proved to be a difficult (and controversial) task because of the lack of a quantitative framework. The present work is an attempt to resolve this issue.
We summarize the features of evolutionary spandrels as follows: (i) they are the byproduct of building rules; (ii) they have intrinsic, well-defined, non-random features; and (iii) their structure reveals some of the underlying rules of construction. As defined, these features can be found in the patterns shown by gene networks, such as the abundance of some particular subsets of integrating genes or “network motifs” which our study suggested that can be explained as a consequence of evolution by gene duplication.
How these results extend to the origins of ecological network patterns? Could the architecture of mutualistic networks be the result of non-adaptive processes? Our starting point comes from appreciating the formal equivalence between “duplication” processes present in cellular graphs and speciation processes in ecosystems. In evolutionary ecology this speciation mechanism corresponds to the process of splitting that leads to two distinct species stemming from their ancestor. While the speciation process is immensely different in nature from the one involved in gene duplication, in mathematical terms such differences become unimportant provided that we look at the process on a sufficiently long time-scale. Moreover, species divergence turns out to be equivalent to a process of link randomisation. Particular to mutualistic networks, two distinct subsets of elements are to be duplicated. Duplication induces a reasonable constraint on the potential interactions expected to be present. For example, if a frugivore eats fruits from a given plant, too many animals using this plant as a resource would rapidly deplete it.
Using a set of simple rules encapsulating these basic precepts, it is possible to show that most architectural features shown by mutualistic webs are well reproduced in a quantitative way. From the pattern of connections to the presence of a nested structure and even the existence of strong asymmetries in the ways that species interact. The agreement is remarkable, and suggests that evolutionary rules of network growth that incorporate the ecological equivalent of the copy-and-paste rule picture are responsible for the global organisation of mutualistic graphs. If true, it would indicate that, along with selection processes operating at the species-species interaction level, macroevolutionary patterns of ecological network changes are likely to shape the entangled bank that Darwin conceived. Selection and adaptation would be operating on top of these evolving webs, whose ultimate origins need to be found in universal, almost mathematical principles of network growth dynamics. Tinkering could therefore be a far-reaching structural principle extending its relevance to the largest scales of organisation of our biosphere. On top of this evolutionary origin, selection processes and ecological-level processes need to be taken into account. Our results do not contradict the reported correlations between nestedness and biodiversity, but rather suggest that the origins of these trends need to be found elsewhere.
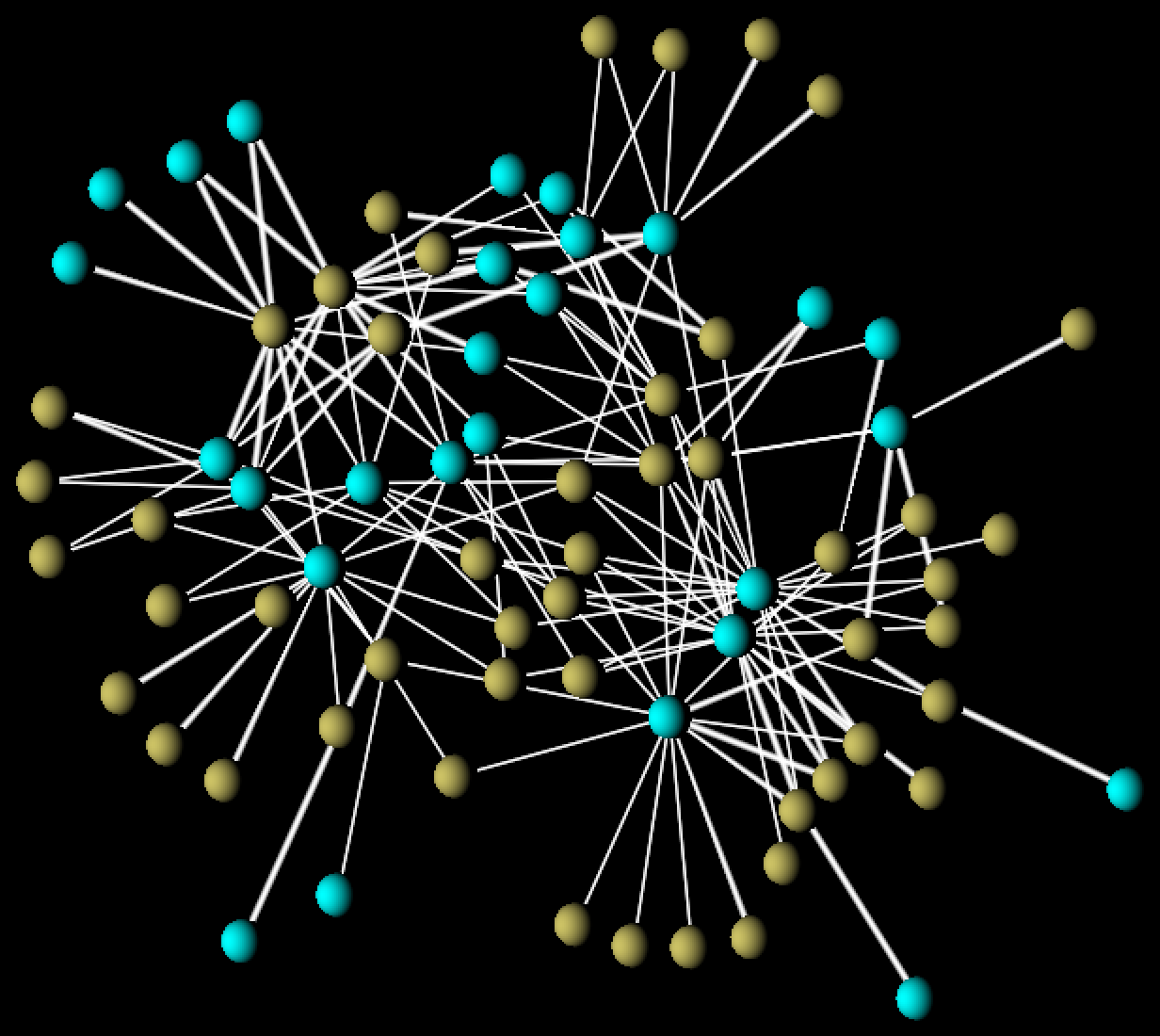
FIGURE 3: a synthetic (generated) network from our model of mutualistic webs. Here ochre and turquoise denote species of plants and pollinators. In the paper, we show how statistical properties of such networks are equivalent to those of real-world networks.
The pattern that emerges from our study of mutualistic webs is also an indication of the presence of universal generative rules. Such universality is well known in physics, where very different systems share common fundamental laws that are capable of explaining their behaviour. Biological systems appear to escape from such picture but the existence of universals has been known in ecology since the first studies on ecological food webs. Diversity and connectivity appear to be related by a universal inverse relation. Similarly, the species-abundance distributions measured from diverse ecosystems are known to follow rather universal trends. The reasons for these regularities could be the result of optimisation, but they are more likely to be the result of instability thresholds or stochastic amplification processes. Our study suggests that something similar occurs when dealing with the evolutionary origins of mutualistic webs. Importantly, this work goes beyond the spandrel metaphor (which has been too often taken literally) by actually measuring patterns in a quantitative way.

Please sign in or register for FREE
If you are a registered user on Research Communities by Springer Nature, please sign in