Three-dimensional non-Abelian Bloch oscillations and higher-order topological states
Published in Electrical & Electronic Engineering and Materials
Bloch oscillations (BOs), a wave packet undergoes a periodic motion in a lattice when subjected to a force, have emerged as a powerful tool for the detection of geometric and topological properties in synthetic lattice systems. This is because BOs are intrinsically related to geometric and topological properties of the underlying band structure. Recently, two-dimensional (2D) non-Abelian BOs have been proposed theoretically in 2D HOTIs through the interplay of non-Abelian Berry curvature and quantized Wilson loops. Meanwhile, new topologically protected edge states emerge on the open boundaries parallel to the body diagonals. The question is whether or not some new phenomena can occur in three-dimensional (3D) HOTIs through the interplay of non-Abelian Berry curvature and quantized Wilson loops.
Recently, some unique topological effects in the 3D HOTIs are unveiled by studying 3D non-Abelian BOs.(https://doi.org/10.1038/s42005-023-01474-9) It is identified that a new type of multiple BOs takes place along the diagonal of the body for the applied force, which is attributed to the finite non-Abelian Berry curvature of the degenerate band structure. Accompanied with these BOs there is a synchronized inter-band beating which is captured by the Wilson loop and can be topologically protected by winding numbers. Furthermore, a new kind of higher-order boundary states appear at the symmetry axes associated with the topological BOs.
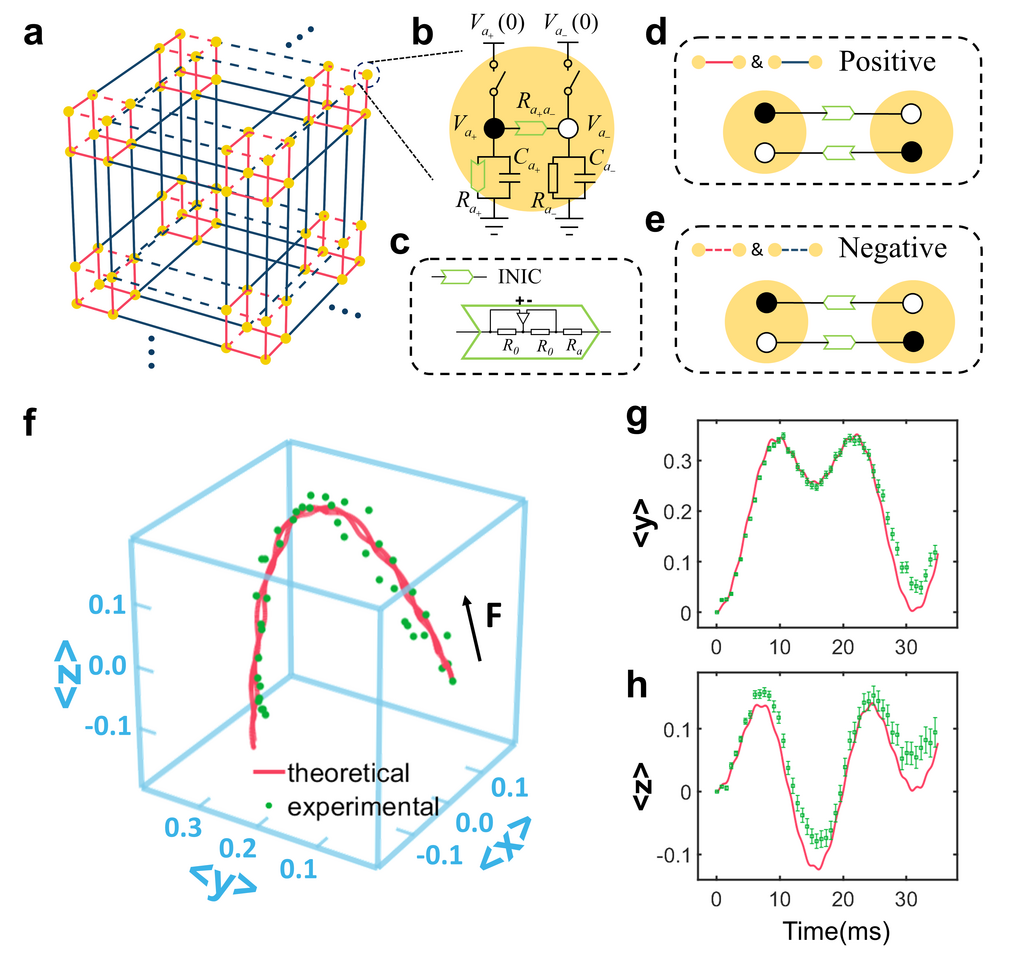
Figure 1 illustrates the schematic diagram for the designed circuit corresponding to the lattice model with an applied force. The voltages at nodes are used to simulate the real-space state in the lattice model. Since the components of the electronic state are complex and the circuit voltages are real, a circuit state consists of voltages of 2n nodes, to correspond to the real-space wavepacket with n sites. These two circuit nodes are connected through a negative impedance converter with current inversion (INIC) to realize the on-site potential. Two pairs of nodes are cross-connected via two INICs, the directions of which depend on the signs of the hopping amplitudes between the corresponding sites, as illustrated in Figs. 1d and 1e. Here, the effective resistances of the INICs are inversely proportional to corresponding parameters (on-site potentials and hopping amplitudes). Moreover, each node is grounded through a capacitor parallel with an INIC or a normal resistor, as shown in Fig. 1b. With the above settings, the evolution of circuit state can be expressed as a Schrödinger-like equation. It can be confirmed that the evolution of voltages on the nodes corresponds to the evolution of the real-space wavepacket in the lattice model.
A circuit system consisting of 216 pairs of nodes is constructed, which corresponds to an open-boundary lattice model consisting of 3×3×3 unit cells with an applied force of Fx = Fy = Fz = –0.4J1. Here, the grounding capacitances are all taken as C0 = 1 µF. The effective resistances of the INICs corresponding to intracell and intercell hopping are set as 1 kΩ and 10 kΩ to realize the hopping amplitudes of J2 = 0.1J1, respectively. The effective resistance of the INIC between the node pair is set as 1/µ to realize the corresponding on-site potential of µ. Furthermore, grounding INICs and resistors are also set appropriately. Under these parameter settings, the BO period for the circuit network is 15.7ms.
Figures 1f, 1g, and 1h displays the evolution for the center-of mass of the circuit wavepacket. The center-of mass along the x direction firstly goes through a rise and fall, and reaches a local minimum at about 16.1 ms, as well as in y and z directions, with the coordinates being (–0.124, 0.254, –0.124). This indicates that the wavepacket completes an oscillation along the applied force F, with the transverse displacement reaching the maximum. Then, the center-of mass experiences another rise and fall in three directions, and reaches a local minimum which basically coincides with the origin, at about 30.9 ms. This reflects another oscillation with an opposite transverse drift bringing the center-of mass back to its initial position. The spatial trajectory of the center-of mass shown by the red curve in Fig. 1f also illustrates this process, where the trajectories of the two BOs basically coincide. The simulated results clearly show that the period-two topological BOs take place in our circuit for the 3D HOTI system, with the period being approximately 30.9 ms, which is consistent with the theoretical result as 2TB = 31.4 ms.
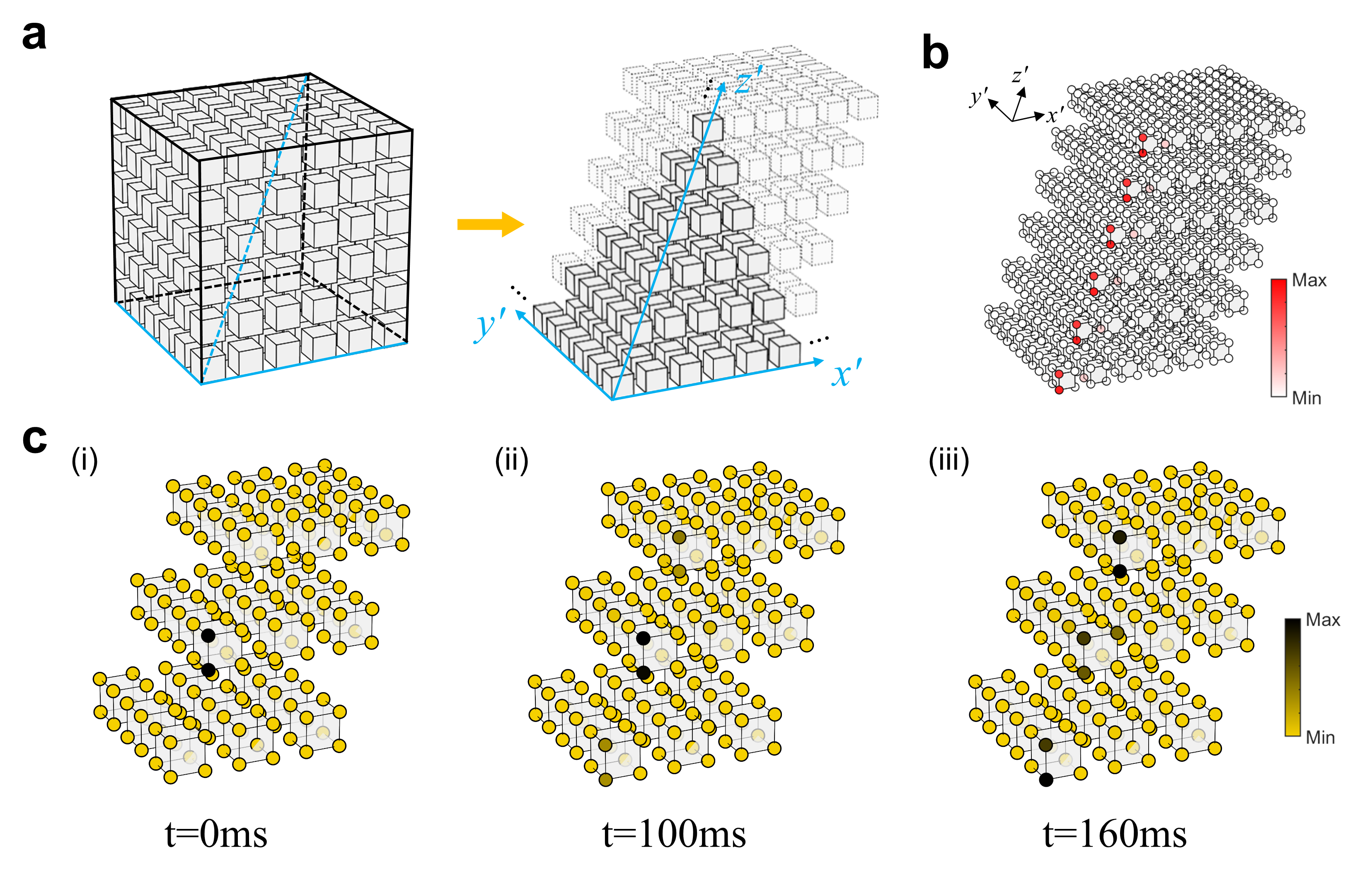
Fig. 2 Novel higher-order boundary states.
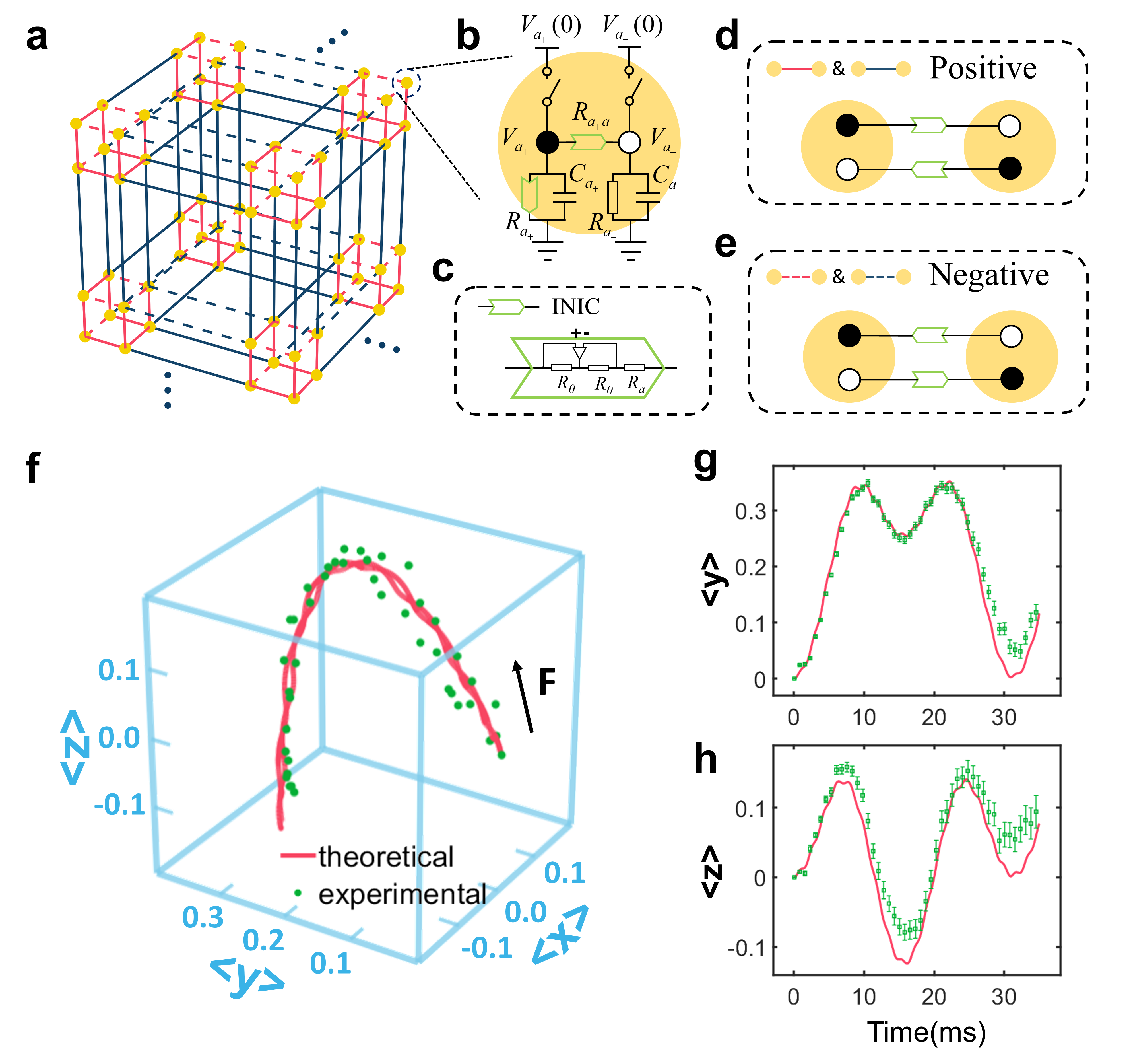
Besides the BO, the novel higher-order boundary states can be found in the three-dimensional system. A system with edges along the body diagonals of the original cubic lattice is given in Fig. 2a. Here, the left part of Fig. 2a shows a schematic diagram of the original cubic stacked structure, with the blue lines indicating the directions of the open boundaries, and the right part of Fig. 2a illustrates the system with new boundaries. The new spatial directions x', y', and z' are chosen where z' is along the body diagonal while the x' and y' directions are the same as the previous x and y directions, respectively.
When J1 < J2, the surface and hinge states can be observed. The electron density concentrated along the hinges of the model but keeping the bulk and surfaces insulating. Such hinge states are two dimensions lower than the system, which are so called “higher-order” boundary states. This kind of higher order boundary states does not exist in the 2D counterpart, since the edges along which the topological BOs take place are one dimension lower than the 2D system. The body diagonal edge states correspond to a vanishing nested Wilson loop invariant but are also topologically protected, which is indicated by the winding number wi who changes the sign when J1 = J2.
To verify the higher-order boundary states, an corresponding circuit network is fabricated which consists of 3×3×3 unit cells with edges along the body diagonal. The voltages at the nodes are stimulated to observe the evolution of state on the outermost two sites of the cell located on the hinge at t = 0 ms, which is shown in Fig. 2c(i). The experimental results of the circuit wavepacket at t = 100 ms and 160 ms are displayed in Figs. 2c(ii) and 2c(iii). It can be seen that the electronic density of the state indicated by the circuit voltages diffuses along the z' direction within a finite time. Regardless of a small amount of voltage signals diffusing to the surface sites due to the influence of circuit disorders, most voltage signals occupy the outermost sites of the unit cells on hinge all the time, which indicates that the one-dimensional hinge state is a mode isolated from the bulk.
Follow the Topic
-
Communications Physics

An open access journal from Nature Portfolio publishing high-quality research, reviews and commentary in all areas of the physical sciences.
Related Collections
With Collections, you can get published faster and increase your visibility.
Higher-order interaction networks 2024
Publishing Model: Open Access
Deadline: Feb 28, 2026
Non-Markovian quantum dynamics in physical systems: description and control
Publishing Model: Open Access
Deadline: Dec 31, 2025



Please sign in or register for FREE
If you are a registered user on Research Communities by Springer Nature, please sign in