Topological Nonlinear Optics with Pseudo Atomic States
Published in Physics
The revelation of topological states of light has emerged as a milestone in quantum optics. As a matter of fact, photons do not respond to the magnetic field because of their neutral nature, unlike the conventional topological materials, but one can analogically engineer topology in light by interacting photons with such structures which lead them to pick different (or opposite) phases. Such topological phases of light have been studied in gyromagnetic photonic crystals, quasicrystals, optical waveguides and recently, in degenerated optical cavities. But it could be very interesting to know what kind of impacts can be induced to transmitting light from pseudo-atomic spin-states. Spin-orbit (SO)-coupled dressed states of Bose-Einstein condensate (BEC) in a single cavity system provide a feasible approach for obtaining synthetic spin-states and quantum nonlinear optical phenomena can be used to create transparencies for synthetic cavity system. The electromagnetically induced transparency (EIT) – quantum interference between two photon transitional paths excited from a single state – is the finest example of such nonlinear quantum optical transparencies.
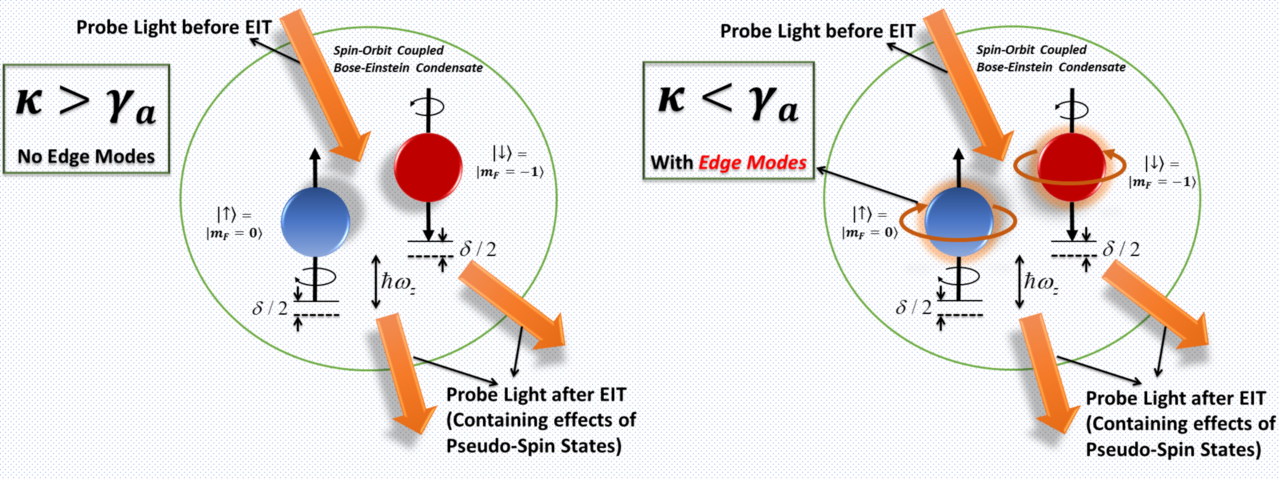
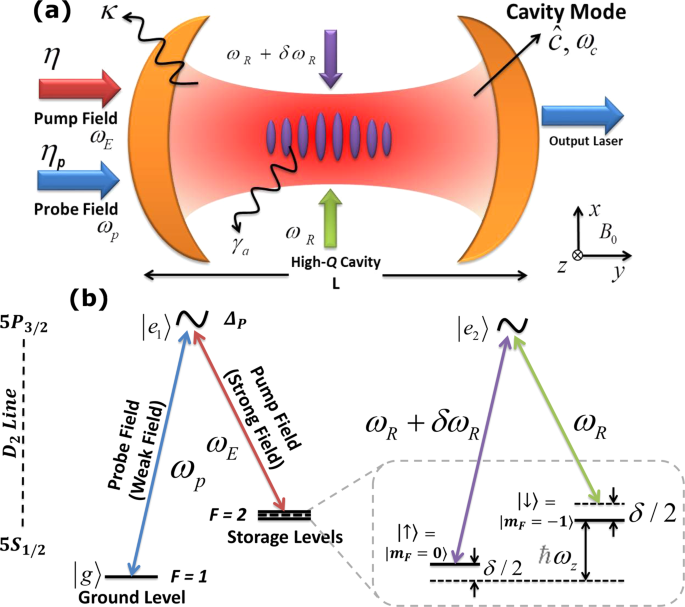
Fig. 1. Schematic illustration of the steady. The spin-orbit coupled Bose-Einstein condensate is trapped inside a high Q cavity, driven by control pump field ωE and a probe field ωP. When probe light interacts with pseudo spin-states, these states imprint synthetic texture to the probe light modes (schematically shown in left figure), which then form gapped and gapless bulk modes. But when the atomic dissipations act as a gain or amplification for probe light (schematically illustrated in right figure), surface modes or edge modes of probe light appear on the edges of the spin-states resulting in topology of light.
In this work, the probe light was used to interact with spin-orbit coupled Bose-Einstein condensate in a cavity system. By adopting the approach of electromagnetically induced transparencies, we observe the transmission of probe light to reveal whether spin texture of spin-orbit coupled atomic states can imprint topological features to interacting probe light or not. The probe-pump induced double excitations of both spin states create transparencies for probe light. After that the pseudo spin states (synthetic spin-up and spin-down) of spin-orbit coupled BEC (in presence of cavity setup and configuration) imprint their signatures in the transmitting probe photons by altering their orbital angular momentum, depending upon the synthetic spin of the atomic states, as schematically illustrated in Fig. 1. However, in amplification case – where the atomic damping greater than cavity decay acts as a gain to the cavity field (κ/γ<1) – a edge-like surface modes appear around the edges of the pseudo-spin states revealing the topological phase transition, as schematically illustrated in Fig. 1 (right).
Transparencies For Probe Light:
To start, the phenomenon of electromagnetically induced transparency occurs because of the quantum interferences that permit the transmission of probe light from atomic medium in presence of pump laser induced transitions.
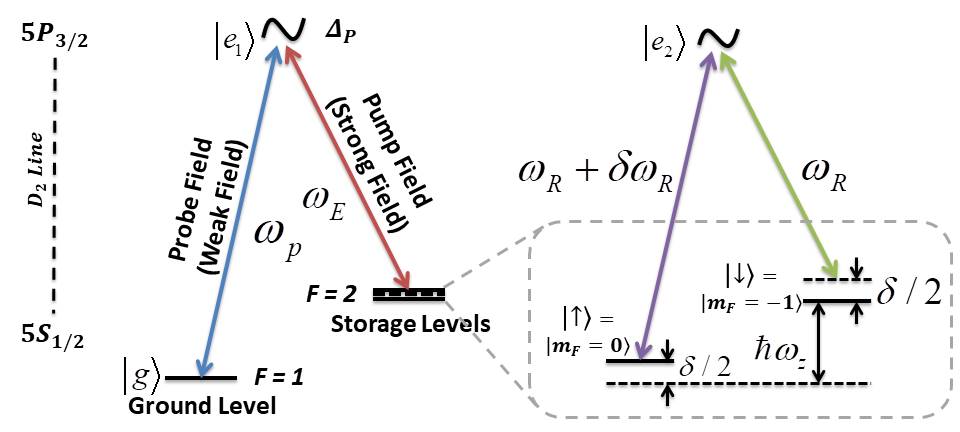
right-side is the Raman excitations at storage level for spin-orbit coupling.
In this study, the bias magnetic field produces a Zeeman splitting ħωz of electronic ground state manifold (as shown in Fig. 2), yielding to two pseudo spin states |↑〉 and |↓〉. These pseudo spin states then become momentum sensitive because of momentum locking produced by the two counter propagating Raman lasers. These pseudo-spin states get collectively excited to the intermediate or storage state, similarly like any conventional mediums for electromagnetically induced transparency. As both pseudo spin states lay at different levels in the spectrum of intermediate storage state because of probe-pump interactions, therefore, the transitions from both states to the ground state of the system |g〉 are prohibited by the dipole configuration, yielding in two transparencies for the probe light. In other words, now quantum interference between three transitional pathways results in two transparencies. Therefore, the first (or only one) transparency window appears in the probe transmission when only Bose-Einstein condensate (without spin-orbit coupling) is coupled to the cavity. However, in the presence of spin-orbit coupling, the probe transmission shows two windows of electromagnetically induced transparency, because of standard Raman process that converts simple Bose-Einstein condensate to two pseudo spin states. Further, at higher values of ωz, the Zeeman splitting reaches to such levels from where the transition blockage to the system ground state |g〉 results in another dark state occurring in off-resonance domain of probe-pump detuning.
Topological Nonlinear Optics:
In order to observe the formation of optical Dirac cones, conventionally, we plot the transmitted light modes (bulk modes) from such structures as a function of spatial wave vector (in reciprocal space) and the transmitted optical mode frequency. Fundamentally, the interaction of optical field with such objects or materials (with multiple invariants or spin texture) will force light to deform its mode spectrum in accordance with the object’s signatures. Such transmitted optical modes (mimicking like bulk states or optical bulk modes) disperse into gapped or gapless Dirac cones, again depending upon the calibration, leading towards the nontrivial topology of light.

Fig.3. Topological Nonlinear Optics with SOC BEC. The transmission amplitude |ε|2 versus kx (x π) and Δp/κ. The first ((a), (d) and (g)), second ((b), (e) and (h)) and third ((c), (f) and (i)) columns illustrate the influence of Ωz = 0.1Ω, 4Ω and 8Ω, respectively, on the bulk modes. While the first ((a), (b) and (c)), second ((d), (e) and (f)) and third ((g), (h) and (i)) rows accounts for δ =0Ω, 3Ω and 3Ω, respectively. The first and second rows correspond to the lossy regime (κ/γ>1) while the third row is for gain regime (κ/γ<1).
As mentioned previously, the pseudo spin states can imprint their features to probe transparencies, so, these imprinted characteristics will force probe transmission modes, or bulk modes, to spatially disperse into gapped and gapless Dirac cones. Figure 3 of the manuscript illustrates these effects. Initially, with weak (or almost zero) Raman coupling, two conventional side-modes appear in the probe transmission but, when we increase Raman coupling, these side modes yield into bulk modes dispersing into gapless Dirac cones, as shown in Figs. 3b and 3c, where the maximum probe transmission modes are bulk modes with Dirac cones appearing around kx = ±2π. The reason behind the emergence of Dirac cones in probe transmission is the phase transition occurring in BEC because of Raman coupling, which imprint similar effects on the probe transmission bulk states leading to gapless Dirac cones with increase Raman coupling. However, when the transition or energy spectrum for BEC become asymmetric with Raman detuning, a gap appears in the probe transmission bulk modes, as can be seen in Figs. 3e and 3f, where Dirac cones are no more gapless.
Further, when we consider the gain regime, where atomic damping is dominating the cavity decay rate (κ/γ<1), the atomic damping induced amplification in probe transmission appears in the form of Dirac-like edge state (or surface states) closing the gap between the edges of the bulk modes and yielding into the nontrivial topology of light, as can be seen around resonance in the lower panel of Fig.3. These edge modes are basically the scattering of the amplified part (or the atomic damping induced contribution) of the probe light from the edges of pseudo spin states. Such optical edge modes are crucial to define the nontrivial topology of light. Further, the active-passive configuration that yields to gain regime and leads to the broken PT-symmetry could also be considered as an argument for such topological edge modes.
Follow the Topic
-
npj Quantum Information

The scope of this journal spans across all relevant disciplines, fields, approaches and levels and so considers outstanding work ranging from fundamental research to applications and technologies.
Related Collections
With Collections, you can get published faster and increase your visibility.
Algorithms, Protocols and Architectures for Early Fault Tolerance
Publishing Model: Open Access
Deadline: Jun 25, 2026
Quantum-Enabled Bioimaging
Publishing Model: Open Access
Deadline: May 04, 2026

Please sign in or register for FREE
If you are a registered user on Research Communities by Springer Nature, please sign in