As a magnetized super-sonic plasma flow emanating from the Sun and filling the heliosphere, the solar wind is found to be turbulent by in-situ measurements from space missions. The solar wind turbulence usually not only satisfies the polarization relationship of Alfvén waves but also embodies multi-order statistics characteristics of turbulence. Based on this, solar wind turbulence is also called imbalanced Alfvénic turbulence, known to occur in astronomy and has an essential influence on laboratory plasmas.

The challenges in the study of imbalanced Alfvénic turbulence concern how energy is transferred (cascaded) between different scales. The collision of bidirectional Alfvén waves is credited as the underlying physical process. Based on this view, researchers have been dedicated to searching for the coexistence of the bidirectional Alfvén waves, which are outward (propagating away from the Sun) and inward (propagating towards the Sun) Alfvén waves, respectively, in the solar wind. However, to date, no clear evidence has been found of their coexistence and interactions. How does imbalanced Alfvénic turbulence originating from the Sun transfer energy from large to small scales, thus providing energy for kinetic scale dissipation? To address this question, we integrate three research methods: spacecraft observations, numerical simulations, and theoretical analysis. We dissect and discover three "non-traditional" characteristics of imbalanced Alfvénic turbulence, which are non-bidirectional Alfvén wave collision, non-critical balance cascade, and non-uniform power-law spectra.

 Firstly, we analyzed the Parker Solar Probe's (PSP) measurements of the pristine solar wind during its perihelion phase. The analysis shows that the pristine solar wind turbulence has the following features: (1) a dominating positive correlation between velocity δV and magnetic field δB; (2) the disturbance of  δZ⁺ describing outward Alfvén waves is much larger than that of δZ^-, which is speculated to be the disturbance of inward Alfvén waves; (3) the averaged spectral index of  δZ⁺ is around -5/3, while that of δZ^-  is about -1; (4) number density is weakly compressible and has an averaged spectral index of about -1. Keeping these in mind, we conduct simulations and successfully reproduce these features.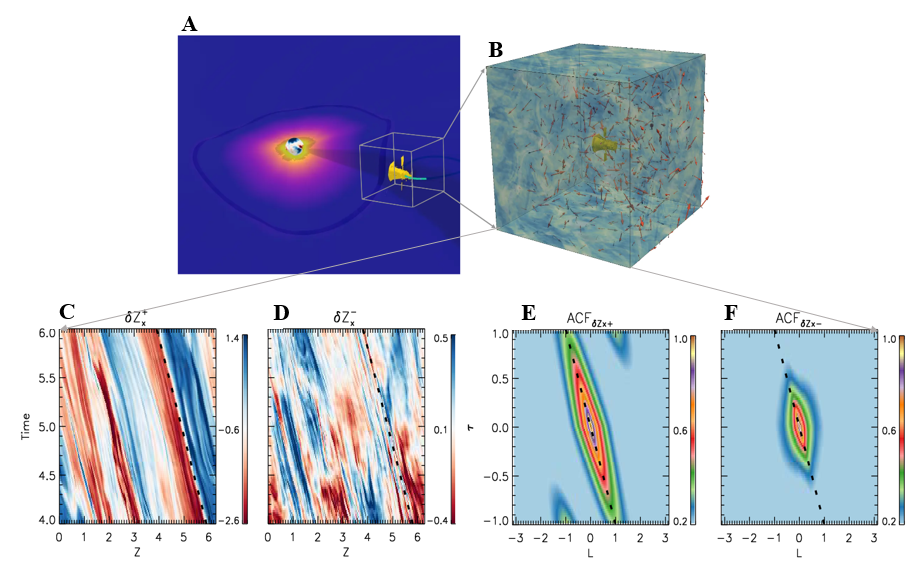Fig.1  A schematic figure of PSP measurements and a simulation of imbalanced Alfvénic turbulence. (A) PSP’s (illustrated in yellow) near-perihelion detection of the pristine solar wind, which is colored by the number density of the solar wind. The Sun is colored by the radial magnetic field. (B) Distributions of the turbulent Elsässer variables (δZ⁺ and δZ^-) in the simulation domain, with the color showing the magnitudes of  δZ⁺ and the arrows denoting the directions of δZ⁺ and δZ^-. (C and D) Time-distance (time-z) diagrams of  δZ_x⁺ and δZ_x^- ; (E and F) Distributions of the auto-correlation function (ACF) of  δZ_x⁺ and δZ_x^-  in the τ (time lag)-l  (spatial lag in the z-direction) plane. The black dashed lines show the expected propagation of Alfvén waves along the z-direction.

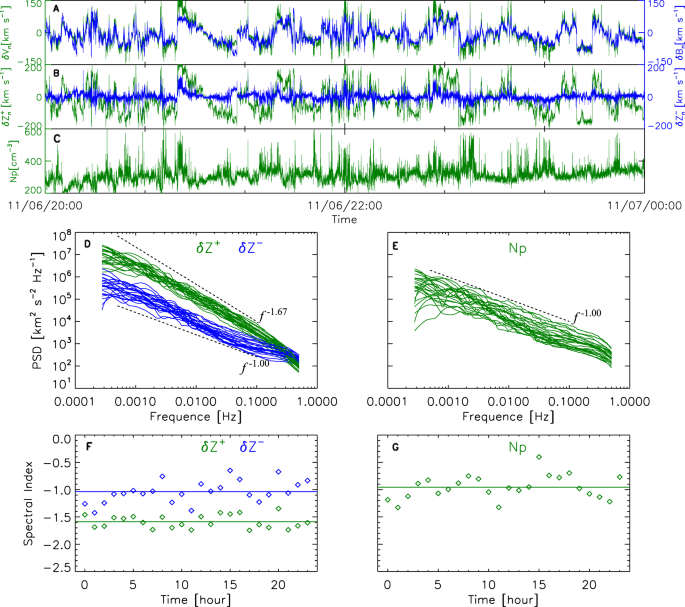
Secondly, by investigating four-dimensional spatiotemporal simulation data, we found that  δZ⁺ and δZ^-  propagate along the same direction with Alfvén speed (Figure 1).      δZ⁺ satisfies the polarization and dispersion relations of Alfvén waves in that direction, pointing out it denotes Alfvén waves. However,  δZ^- does not satisfy these relations. What is the nature of δZ^-? How is the co-propagation of  δZ⁺ and δZ^-  generated? To answer these questions, we further analyzed the spatial distribution of various terms in the control equations of  δZ⁺ and δZ^-  as well as their temporal evolution (Fig. 2). We found that for δZ⁺, the linear term dominates over the nonlinear term, while for δZ^-, it is reversed, indicating non-critical balance nature of imbalanced Alfvénic turbulence. Meanwhile, we found that the nonlinear term, not the compressive terms, generates  δZ^- and causes  δZ^- and  δZ⁺ to propagate in the same direction. This evidences that δZ^-  is not inward Alfvén waves, but a kind of accompanying "co-propagating anomalous disturbance".  As  δZ^- and  δZ⁺  propagate in the same direction, their nonlinear interactions are more effective than when they propagate in opposite directions.

Fig. 2 Direct comparison of the spatial distribution (and wavenumber spectra) and temporal evolution of various terms in governing equations of Alfvénic turbulence.

Finally, we examined the energy transfer rate of  δZ⁺ and δZ^- at different scales to explore the scale locality and non-locality of turbulent cascades. Scale locality and non-locality imply that the energy cascade is completed by nonlinear interactions of disturbances with adjacent or non-adjacent wave numbers. The study found that for Alfvén waves δZ⁺, the energy cascade is accomplished by disturbances of adjacent wave numbers, i.e., fulfilling the scale locality of the energy cascade. However, for the co-propagating anomalous disturbance δZ^-, the energy cascade requires the involvement of large-scale disturbances, not fulfilling the scale locality of the energy cascade. Based on this result, we provided a reasonable theoretical explanation for the different spectral indices of  δZ⁺ and δZ^-  in simulations and observations.

Our research reveals a new mechanism for the energy cascade of imbalanced Alfvénic turbulence: coherent interactions between Alfvén waves and accompanying co-propagating anomalous disturbances transfer energy from large to small scales. This unveils the energy transfer physics of imbalanced Alfvénic turbulence, which is significant for understanding the influence of turbulence on solar wind heating and acceleration, the shaping of the heliosphere, and solar-terrestrial as well as solar-planetary space weather activities.