Agent-based models (ABMs) are widely used for their ability to capture individual heterogeneity, interaction, and adaptation within complex systems. By allowing agents to respond to each other and their environment, ABMs reveal how systemic patterns emerge over time. They generate outputs at micro, meso, and macro levels, reflecting rich temporal dynamics. However, this complexity and multi-level structure pose challenges for traditional global sensitivity analysis (GSA) methods. Global sensitivity analysis (GSA) helps identify which input parameters most influence model uncertainty, improving model development and experimentation. For example, in a COVID-19 model, only 19 out of 940 parameters significantly affected outcomes. While time-varying GSA has been introduced to track changing sensitivities over time, it struggles with interpreting non-linear dynamics and fails to capture the full temporal evolution of model behavior. Additionally, no current GSA method fully addresses the multi-level structure of ABMs, such as sensitivity at agent or community levels. Although spatial variance-based GSA shows promise, it is difficult to adapt for non-spatial ABMs.

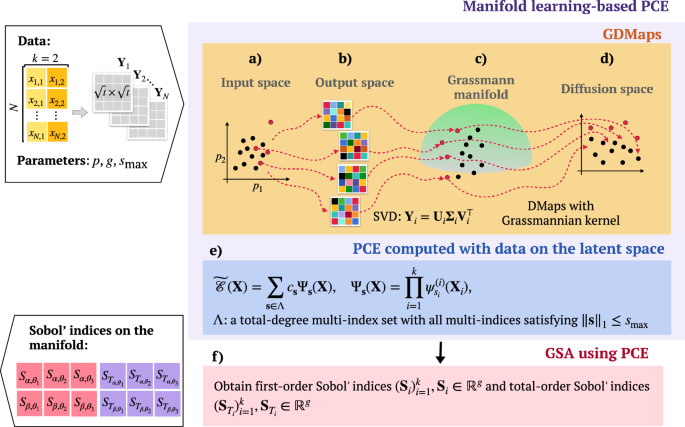
This research presents a novel framework for global sensitivity analysis (GSA) in agent-based models (ABMs), capturing their complex dynamics. The study finds that this method allows for a more comprehensive estimation of parametric sensitivities across different levels. The paper introduces a new GSA framework that leverages Grassmannian diffusion maps and sparse polynomial chaos expansion (PCE) to handle the unique features of ABMs. It effectively reduces data dimensionality and computes sensitivity indices for stochastic inputs. Key findings include its application to diverse models, demonstrating versatility, and its ability to span sensitivities from individual agents to entire populations. However, more work is still needed to fully integrate these techniques into routine practice, this study provides a robust toolset for enhancing model analysis and decision-making in ABMs. Read the full article here.

https://www.nature.com/articles/s41598-024-64331-x