Characterising the intelligence of biological organisms remains challenging yet crucial. The three major theories of intelligence—dynamical systems of neural networks, statistical inference view of the brain as proposed by the free-energy principle¹, and the Turing machine, a basic computational model—have been considered almost independently. Herein, the present work “Triple equivalence for the emergence of biological intelligence²” mathematically demonstrated the triple equivalence between the three concepts. This suggests that a class of canonical neural networks can acquire various intelligent algorithms in a self-organising manner through the statistical inference of Turing machines in the external world. These results provide insights into the neural mechanisms of statistical inference and algorithmic computation and expand our understanding of human and animal intelligence.

Background

Biological intelligence arises from the dynamics of neurons and synaptic connections that can be expressed as differential equations. Moreover, biological intelligence is formed through evolution, which is driven by the selection of individuals who pass on more genes to the next generation. However, an exact description of the intelligent algorithms emerging from such evolutionary processes has yet to be established.

According to the free-energy principle, the perception, learning, and action of all biological organisms are determined to minimise variational free energy. This results in biological organisms performing variational Bayesian inferences in a self-organising manner. From this perspective, these organisms optimise their perception and action by building a generative model in their brains that represents the dynamics of the external world.

We previously identified a biologically plausible energy function from the neural activity equations of canonical neural networks³ and demonstrated its mathematical equivalence to the variational free energy. This indicates the validity of the free-energy principle⁴ for mechanical phenomena at the neuronal and synaptic levels. Such a dynamical system that can be read as performing a Bayesian inference of the external world is referred to as a Bayesian dynamical system.

Nonetheless, whether the free-energy principle alone can achieve sufficient intelligence remains unclear. Gaps remain between the optimisation of perception and action based on the statistical inference and generic intelligence. Previous works on the free-energy principle have not determined whether biological neural networks can acquire arbitrary algorithms. Therefore, the present work considered whether canonical neural networks can acquire general algorithms in a self-organising manner.

Findings

Initially, an energy function for a class of Turing machines was considered. A differential equation whose fixed point expressed the transition mapping of a Turing machine was defined, and its integral was computed to reconstruct the Helmholtz energy. Interestingly, these Turing machines have the Helmholtz energy in a shared functional form with that for a class of canonical neural networks. Therefore, these canonical neural networks can implement Turing machines through their neural activity and plasticity (Fig. 1).

In this correspondence, the neural activity x_t in the middle layer can be interpreted as encoding the automaton states, the synaptic connections in the output layer as encoding memory, and the neural activity y_tin the output layer as encoding memory readouts. Neural activity in the output layer reads memory information by generating mental actions, which are transmitted to the middle layer to alter the internal representation. Furthermore, memory writes can be represented using fast Hebbian synaptic plasticity and its modulations.

In particular, canonical neural networks with two mental actions can construct a universal Turing machine that imitates the behaviour of other Turing machines by separately storing the transition mappings of several external Turing machines. Therefore, this class of canonical neural networks can in principle represent arbitrary algorithms, as well as universal Turing machines.

Notably, the Turing machines considered here can be viewed as a Bayesian dynamical system because it minimises an energy function. These canonical neural networks and Turing machines perform Bayesian inference based on partially observed Markov decision processes (POMDPs), a widely used generative model. The automaton and memory states are represented as posterior expectations. Therefore, the triple equivalence between the mathematical representations of canonical neural networks, variational Bayesian inference under a class of POMDPs, and the Turing machines was established (Fig. 1). This equivalence confirmed that canonical neural networks can perform variational Bayesian inferences of external Turing machines in a biologically plausible manner.

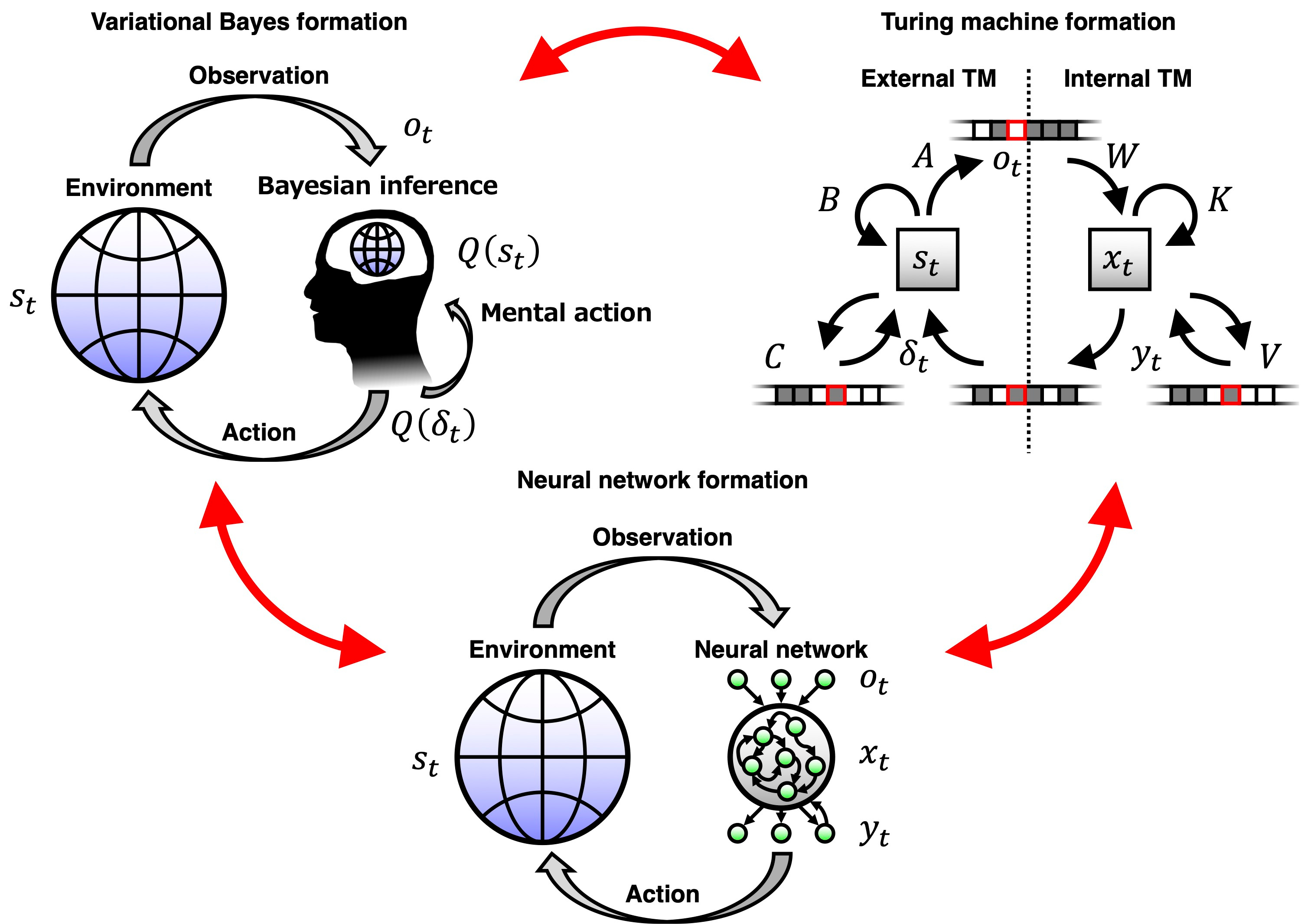
Fig. 1. Schematic of triple equivalence. (Bottom) A dynamical system of canonical neural networks interacting with the external world. (Top left) Brain model based on variational Bayesian inference of the external world as proposed by the free-energy principle. The brain infers the external world using a generative model. (Top right) Interaction between external and internal Turing machines. There is a one-to-one correspondence between these three almost independently developed theoretical concepts.

Furthermore, from an evolutionary perspective, this work suggests that adaptive algorithms—including Bayes-optimal inference and decision making—emerge through natural selection. Population-level Helmholtz energy can be defined by integrating the above-defined Helmholtz energy for individuals and the evolutionary fitness function. This Helmholtz energy also corresponds to the population-level variational free energy. Thus, selecting individuals through natural selection corresponds to optimising the generative model using Bayesian model selection. This allows for the characterisation of the adaptive algorithm (i.e., the generative model) arising from natural selection as a variational Bayesian inference of the states of the Turing machine in the external world.

These propositions are corroborated by numerical simulations of algorithm implementation and neural network evolution. For example, when an external algorithm is an adder, canonical neural networks could self-organise (evolve) to imitate it through natural selection. This provides insights into how adaptive algorithms emerge through evolution.

Perspectives

The virtue of canonical neural networks lies in their utility for mental actions and fast plasticity to read and write programs depending on a context, imitating the diverse algorithms of the external world. This contrasts with traditional neural circuit models that execute a single algorithm based on a fixed generative model. Although the algorithms of the environment and other agents cannot be directly observed, canonical neural networks can naturally perform Bayesian inferences of these algorithms from their behaviour and responses. This suggests that canonical neural networks can in principle acquire generic intelligent algorithms in a self-organising manner. This notion will provide a universal characterisation of biological intelligence emerging from evolutionary processes in terms of Bayesian model selection and belief updating.

References

1. Friston, K. J. The free-energy principle: a unified brain theory? Nat. Rev. Neurosci. 11, 127-138 (2010). https://doi.org/10.1038/nrn2787
2. Isomura, T. Triple equivalence for the emergence of biological intelligence. Commun. Phys. 8, 160 (2025). https://doi.org/10.1038/s42005-025-02059-4
3. Isomura, T., Shimazaki, H. & Friston, K. J. Canonical neural networks perform active inference. Commun. Biol. 5, 55 (2022). https://doi.org/10.1038/s42003-021-02994-2
4. Isomura, T., Kotani, K., Jimbo, Y. & Friston, K. J. Experimental validation of the free-energy principle with in vitro neural networks. Nat. Commun. 14, 4547 (2023). https://doi.org/10.1038/s41467-023-40141-z

Additional information: This blog post is based on a translation of the following press release (in Japanese): https://www.riken.jp/press/2025/20250417_1/