Ultracold chemical reactions in a quantum gas
Published in Physics

In recent years, ultracold molecules have been gaining attention due to potential applications in quantum simulation, quantum information processing, precision measurement and many more. Ultracold molecules in the quantum degenerate regime offer us the chance to explore complex quantum phenomena and steer chemical reactions.
Quantum degeneracy (for bosonic particles) refers to the phenomenon where the particles all occupy the same lowest energy quantum state. For quantum degenerate fermionic particles, they cannot occupy the same quantum state due to the Pauli exclusion principle but they will continue to fill the lowest quantum states until reaching some maximum energy level known as the Fermi energy. In such a quantum regime, bosonic particles evolve as a single particle and exhibit collective dynamics.
The first example of ultracold molecules in the quantum degenerate regime was demonstrated by the Ye group at JILA in which they cooled a bulk gas of fermionic KRb molecules [1]. This was followed by the production of a degenerate Fermi gas of NaK molecules at MPQ [2].
In our previous work [3], we reported on the observation of a Bose-Einstein condensate (BEC) of Cs2 molecules in a highly excited rovibrational state. These molecules are produced by pairing atoms in the atomic BEC into molecules with the help of magnetically tunable Feshbach resonances. Feshbach resonances occur when the total energy of two colliding atoms closely match the energy of a diatomic molecular bound state. By simply changing the magnetic field, we can convert two atoms into one molecule. Starting with an atomic BEC, we observe the formation of a stable molecular BEC near the resonance. We attribute the stability of the molecular BEC to the trap geometry and the low temperature. The transition we realized between the atomic and molecular condensates is analogous to the Bardeen-Cooper-Schrieffer (BCS) to BEC crossover in a fermionic superfluid. The BCS state refers to weakly bound pairs of fermions which can be coupled together using Feshbach coupling to form a molecular BEC.
In our new work, we explore chemical reactions in the quantum degenerate regime which are expected to be drastically different from that in a thermal gas. In a normal gas, the rate of chemical reaction depends on the temperature, which is described mathematically by the Arrhenius equation. At lower temperatures, the rate constant should be suppressed which indicates that the chemical reaction should slow down. When we approach zero absolute temperature, we should expect few chemical reactions to occur. However, this is not true in the quantum degeneracy regime. For example, if Bose-condensed atoms are coupled to Bose-condensed molecules, theory predicts large amplitude coherent oscillations between these two quantum matters. This phenomenon, as known as “quantum super-chemistry”, describes Bose-enhanced non-Arrhenius chemical kinetics at very low temperatures [4].
The reaction dynamics can be described by two processes. The first one is Feshbach coupling which converts two atoms into one molecule and vice versa. The second one is three-body recombination where three atoms collide together to form a diatomic molecule and a free atom each carrying kinetic energy. To supplement our understanding of the reaction dynamics of the coupled atomic and molecular matter wave fields, we introduce an “energy conservation” law which is derived from the equations of motion in which the kinetic and effective potential energy terms are both dependent on the molecule population. We dub the effective potential as the many-body reaction potential where we start with a pure sample of atoms or molecules which eventually relaxes towards the potential minimum and equilibrates at the minimum with small amplitude coherent oscillations (Fig 1). The reaction potential and the oscillation frequency near the minimum scales with the particle number which indicates the bosonic enhancement of the reaction dynamics.
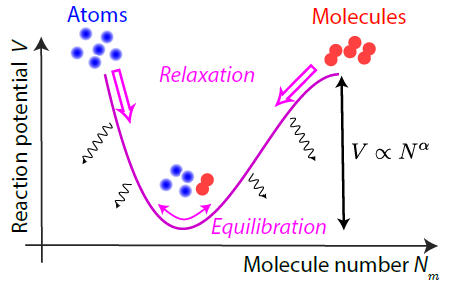
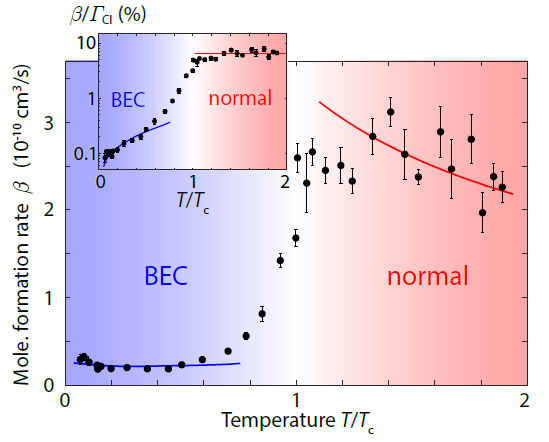
In this paper, we show experimentally that these coherent oscillations occur between Bose condensed Cs atoms and Cs2 molecules. We initiate the reaction by quenching the magnetic field near the narrow g-wave Feshbach resonance which couple atoms into diatomic molecules. By comparing the molecule production rate below and above the BEC critical temperature (Fig 2), we see that there is a clear difference in chemical reactions taking place in the quantum degeneracy regime versus the normal gas regime. The molecule production rate coefficient in the normal gas regime scales with temperature in an expected way whereas it drops off steeply once we cross over into the quantum degeneracy regime.
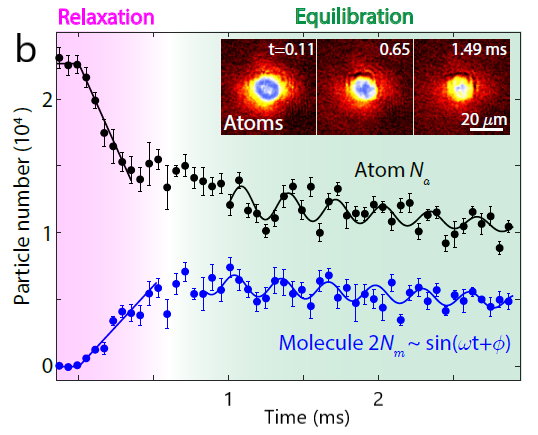
We also studied atom loss around the resonance which uncovered interesting features in the atom-molecule coupling. As the magnetic field is quenched closer to the resonance, the atom loss increases drastically. We plotted the atom loss rate as a function of the magnetic field which shows a Lorentzian line shape (Fig 3a). We attribute this line shape to Feshbach coupling. Interestingly, we measured enhanced atom loss slightly below the resonance which we identify as a fast relaxation towards the potential minimum in the many-body reaction potential; these relaxation dynamics stem from three-body relaxation.
Following the relaxation, both atom and molecule populations settle to a certain value and subsequently begin small amplitude oscillations (Fig 3b). These oscillations are consistent with our predictions that atom and molecule populations experience small amplitude oscillations as they equilibrate near the minimum of the reaction potential. The frequency of these oscillations is dependent on the magnetic field detuning. As we quench further away from the resonance, the frequency approaches the molecular binding energy. On resonance, the molecular binding energy is zero, but the measured frequency itself is nonzero, given by the coupling strength between atomic and molecular matter wave fields.

To demonstrate bosonic enhancement, we probe the atom-molecule coherent oscillations on resonance with different initial atom number. After initiating the reaction, we observe that samples with a higher initial atom population and density displayed faster oscillations (Fig 4a). This oscillation frequency around the minimum is determined by the curvature of the reaction potential which itself is dependent on the particle number. In our model, we consider both two-body and three-body processes and determine the reaction potentials individually. From these potentials, we can extract the oscillation frequency as a function of the particle number. We find that the three-body model fits our measurements better (Fig 4b). In addition, the potential minimum of the reaction potential is different depending on the models. In the three-body model, the potential minimum is situated at fm=1/5, whereas in the two-body model, the potential minimum is situated at fm=1/3 where fm denotes the fraction of the number of molecules over the total particle number (which includes both atoms and molecules). In Fig.4c, the molecule population settles at fm=1/5 which is consistent with the findings of our model. The potential minimum as a function of the molecule fraction doesn’t change regardless of initial particle number.
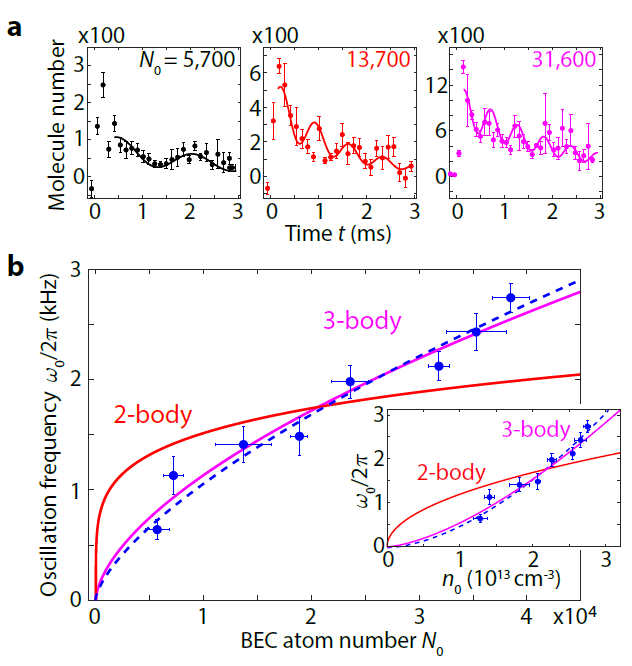
Fig. 4 (a) Bose enhancement with different particle number. (b) Extracted oscillation frequencies as a function of the particle number. Solid lines are fits given by our models.
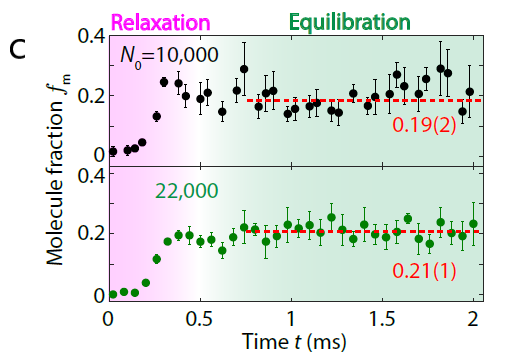
Fig. 4(c) Evolution of molecule fraction fm for different initial atom number.
In conclusion, we observed many-body chemical reactions between ultracold atoms and molecules in the quantum degenerate regime. The oscillations between atomic and molecular matter wave fields indicate quantum coherence and its frequency dependence on the particle number indicates Bose enhancement. The coherent atom-molecule coupling and Bose enhancement are two important features of the conjectured “Quantum super-chemistry". The reaction dynamics are well described by the three-body recombination process. We hope that this work helps improve our understanding of the dynamics behind ultracold chemistry.
References
[1] Luigi De Marco, et al. A degenerate Fermi gas of polar molecules. Science 363, 853-856(2019).
[2] Schindewolf, A. et al. Evaporation of microwave-shielded polar molecules to quantum degeneracy. Nature 607, 677-681 (2022)
[3] Zhang, Z., et al. Transition from an atomic to a molecular Bose–Einstein condensate. Nature 592, 708–711 (2021).
[4] Heinzen, D. J., et al. Superchemistry: Dynamics of coupled atomic and molecular Bose-Einstein condensates. Phys. Rev. Lett. 84, 5029-5033 (2000).
Follow the Topic
-
Nature Physics

This journal publishes papers of the highest quality and significance in all areas of physics, pure and applied.


Please sign in or register for FREE
If you are a registered user on Research Communities by Springer Nature, please sign in