Consider the manuscript processing in a journal; the editor usually needs to “integrate” the comments from multiple reviewers to gain “information” about the manuscript’s value.
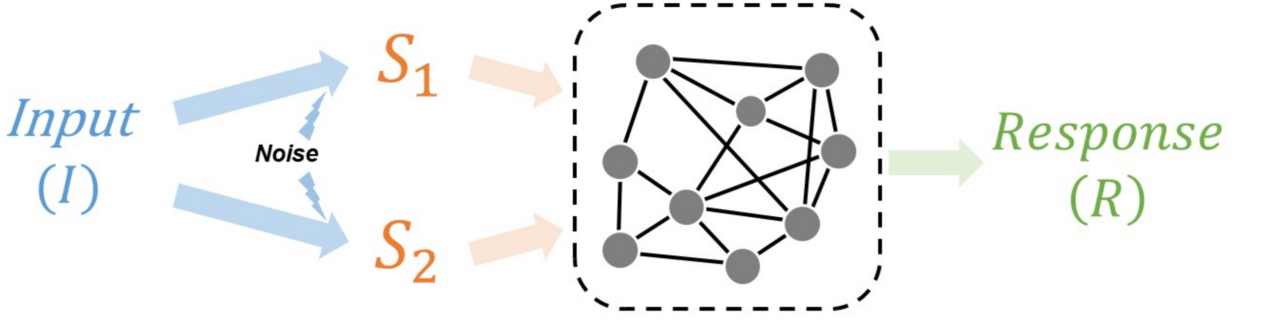
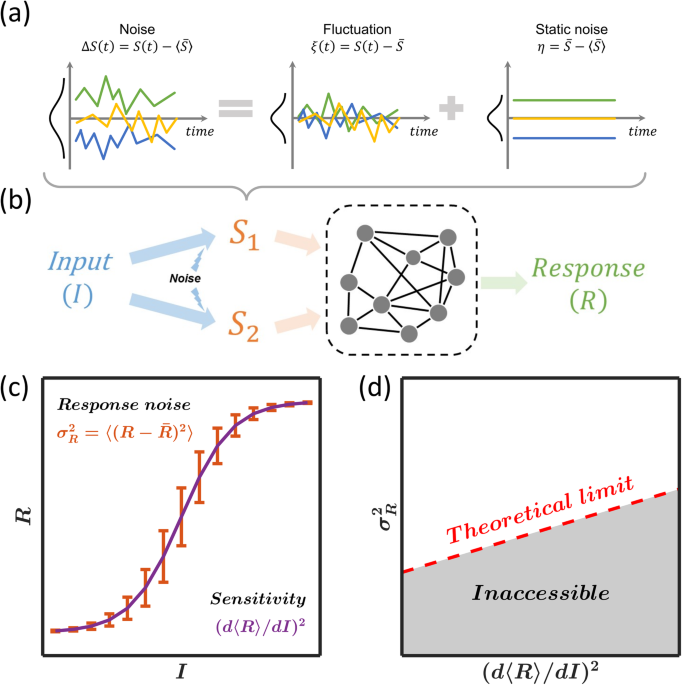
Information integration is ubiquitous in our daily lives, as in the example above. How can we achieve the optimal information integration to make the best decision? The mathematics behind optimal integration intrigues us. In our paper, we delve into a prototype of information integration (figure below). In this framework, a “response module” (akin to the editor in the manuscript processing example) reacts to the input which, however, is usually unobservable (such as the true value of a manuscript). Therefore, multiple intermediate signals (the reviewers’ comments) are involved in encoding and relaying the input to the response module. The more intermediate signals involved, the more information the response module could gain, as each intermediate signal might unavoidably contain “noise”. How should the response module integrate these signals to maximize information?
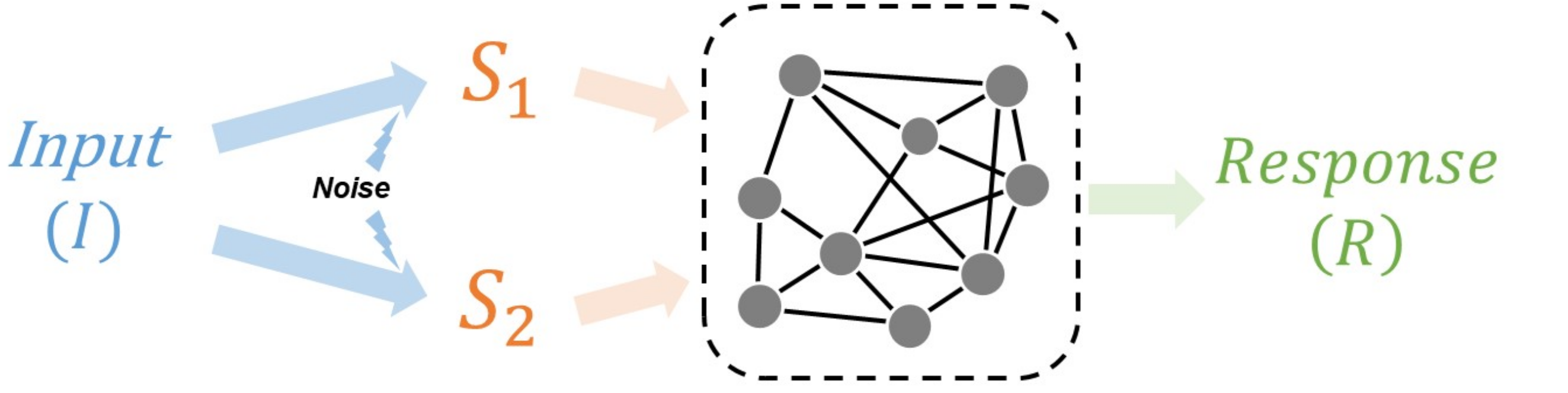
In our paper, we first discovered that the response noise is constrained by the sensitivity to the input, where both response noise and sensitivity are closely related to the amount of information transmitted. We further analytically derived the optimal strategy to achieve minimal noise by applying the phase diagram representation of a complex system, which is consistent with straightforward intuition: the weight of an intermediate signal should positively correlate with its precision. Based on the optimal strategy, we can theoretically predict how the response is affected when perturbing the intermediate signal.
Application to fly embryo development
The discovered optimal strategy finds its application in fly embryo development. In the development of fly embryos, thousands of nuclei have to express different genes, adopt different cell fates, and ultimately develop into different body structures. The major requirement is that these behaviors have to be in line with their physical positions in the embryos. For example, the fly’s head has to be at the front, not the middle, of its body. How can the nuclei know their positions? Mother nature has evolved a fascinating and elegant mechanism known as the morphogen gradient to provide positional information. Through relatively simple processes, morphogens, a specific type of protein, can exhibit a nonuniform concentration distribution inside the fly embryos, acting as a landmark. By “looking” at this distribution, the nuclei can “guess” their positions.
To increase the precision in the position guessing and the subsequent development, more than one morphogen is involved in the fly embryos. Based on the theoretical framework studied before, we derived an optimal strategy for the underlying gene network to minimize position guessing noise by reading these morphogen concentrations. Assuming the fly embryos do follow the optimal strategy, we can predict quantitatively how the developmental patterns of the embryo will change if we experimentally perturb one of the morphogens. The alignment observed between our prediction and experimental data suggests that embryonic development could be optimal.
Modeling insights
Our modeling approach to address the developmental pattern in the fly embryos opens a potentially new avenue for predictive biological modeling. One straightforward way to predict the behavior of a system is to model it from the bottom up. However, bottom-up modeling requires a significant amount of prior knowledge about the system of interest, which may not always be available. In scenarios like morphogen information integration in fly embryos, the response of a gene network to an external perturbation can be nicely predicted after constructing the gene network model. However, it usually faces the risk of overfitting and is computationally expensive, if possible, to build such a model based on a detailed description of the underlying gene-gene interactions. On the other hand, the noise properties, combined with the optimality principle, are precise enough to predict the response behavior of such a complex network, even if we know nothing about the underlying interaction between genes. Overall, we hope our research can serve as an example supporting that highly coarse-grained models could have similar potential in predicting biological systems’ behavior as the classic detailed models.
Follow the Topic
-
Communications Physics

An open access journal from Nature Portfolio publishing high-quality research, reviews and commentary in all areas of the physical sciences.
Related Collections
With Collections, you can get published faster and increase your visibility.
Higher-order interaction networks 2024
Publishing Model: Open Access
Deadline: Feb 28, 2026
Non-Markovian quantum dynamics in physical systems: description and control
Publishing Model: Open Access
Deadline: Dec 31, 2025





Please sign in or register for FREE
If you are a registered user on Research Communities by Springer Nature, please sign in