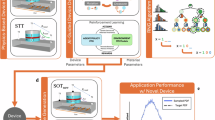
When we first began exploring magnetic tunnel junctions (MTJs), our goal was not to build an optimization solver. MTJs were familiar to us as memory elements - tiny devices where electrons tunnel through an insulating barrier depending on the magnetic orientation of two layers. Yet very early on, we noticed a different personality hidden within these devices: under certain pulse conditions, they switch randomly. Not unpredictably in the chaotic sense, but probabilistically - with a well-defined, tunable chance of flipping from one magnetic state to another.

This small observation eventually grew into the work that became our paper Probabilistic Greedy Algorithm Solver Using Magnetic Tunneling Junctions for Traveling Salesman Problem. In hindsight, it feels obvious: if the physics generously provides randomness - and even lets us control its statistical shape - why not use it directly to solve problems that require stochastic exploration?

But the path to this realization was anything but straightforward.

From memory devices to “physical dice”

One of the foundational motivations came from the widespread use of randomness in optimization and machine learning. Algorithms like simulated annealing and genetic algorithms rely on random sampling to explore the landscape of possible solutions. The better the randomness - and the better we can control it - the more efficient these algorithms can become.

Most computing systems today rely on pseudo-random number generators, which are deterministic algorithms pretending to be random. They are convenient, but they cannot truly vary their distributions without extra software steps. In probabilistic algorithms, this mismatch becomes a bottleneck.

MTJs, on the other hand, provide randomness at the level of physics. The device switches not because of a software rule, but because thermal agitation pushes it over an energy barrier. More importantly, we realized that by adjusting the voltage or pulse conditions, we could smoothly tune the switching probability from near 0% to near 100%. This effectively made each MTJ a probabilistic bit, a p-bit, with a tunable output distribution.

This idea echoed earlier conceptual work on stochastic magnets for probabilistic computing, but we wanted to take it a step further: could we embed such hardware randomness into a full optimization routine, not just simulations?

The Traveling Salesman Problem (TSP) offered the perfect testbed.

Why TSP again?

The TSP has been solved countless times in countless ways. Yet it remains compelling not because we cannot solve small instances, but because it forces us to confront scalability. The number of possible routes grows factorially with the number of cities, making brute force impractical even for moderately sized problems.

Greedy algorithms make local decisions, choosing the nearest next city, but often get stuck in poor solutions. More advanced methods introduce randomness, but their efficiency depends heavily on how randomness is injected and controlled.

We wondered: What if the randomness came directly from hardware, and could adapt its probability distribution at each step of the algorithm?

This question became the seed for the “probabilistic greedy algorithm” we developed.

A hybrid between intuition and physics

In our solver, each decision, choosing the next city, is not a simple nearest-neighbor rule, but a probabilistic choice. The probability of picking a city is influenced by the distance to it and a temperature-like parameter k_BT that controls the level of exploration. At low temperature, the algorithm behaves almost deterministically. At high temperature, it wanders freely. In between lies a window where good solutions are found efficiently.

The challenge was that the required probability distribution changes at every step of the route. Traditional random number generators would require repeated transformations from uniform distributions, adding software overhead. But MTJs, with their tunable switching curves, allowed us to directly generate random samples matching the updated distributions.

This became the conceptual breakthrough: Instead of forcing hardware to emulate software randomness, we shaped hardware randomness to match the algorithm.

To our delight, this approach not only worked - it often outperformed classical simulated annealing and genetic algorithms in both solution quality and convergence speed.

Unexpected challenges along the way

Working with real MTJ devices introduced practical hurdles.

First, each device has slight variations in switching behavior. What looks like a 50% switching probability on Monday might drift to 47% by Thursday. To tame this instability, we developed self-stabilizing feedback routines and pulse-width modulation schemes that could maintain a target probability distribution even as conditions changed.

Second, integrating laboratory instrumentation with real-time probabilistic decision-making required building a control environment from scratch. We used a National Instruments PXIe system connected through a probe card interface, and created a Python framework to manage device operations, collect measurements, update probability distributions, and drive the algorithm loop.

Finally, while solving a 14-city problem experimentally was feasible, scaling to 70 cities required algorithm-level simulations. But these simulations revealed something encouraging: the hardware-inspired algorithm scales better than expected, hinting that a future FPGA or ASIC implementation could handle even larger problems in real time.

A surprising analogy: MTJs and large language models

One of the more amusing reflections came late in the project. The iterative structure of our solver - making one selection at a time, based on a dynamically updated probability distribution - resembles how large language models generate text token by token. In both cases, a softmax-like probability landscape guides the next step. The parallel is not perfect, but it sparked exciting conversations within our team about whether spintronic randomness could someday accelerate AI inference tasks involving stochastic sampling.

These speculative ideas reminded us that interdisciplinary inspiration often arises from unexpected corners.

Looking ahead

Our work does not claim to solve TSP universally or outperform all meta-heuristics. Instead, its contribution lies in showing that physical randomness, when both high-quality and tunable, can directly enhance heuristic search. This opens doors to hardware accelerators that use stochastic physics as a computational resource rather than a nuisance.

The next steps are clear: implementing the solver on FPGA or ASIC platforms, exploring larger MTJ arrays, and testing applications beyond TSP, such as graph coloring, scheduling, and probabilistic AI models.

Most excitingly, this project reaffirmed a belief we shared from the beginning:
when we listen closely, materials often tell us how they want to compute.