Beyond the traditional charge measurement via shot noise in the fractional quantum Hall regime
Published in Physics

Finding the charge of the carriers participating in the transport appears to be one of the most fundamental questions. It may sound trivial as the elementary particle carrying the current is the electron with charge e=1.6×10-19 Coulomb. But due to interactions, born exotic states of matter may support quasiparticles with charges different than the electronic charge e. For instance, in trivial superconductors, paired electrons with charge 2e are the effective quasiparticles. Similarly, in the fractional Quantum Hall effect (FQHE), fractional states support quasiparticles with a fractional charge of the electron.
The most reliable method to determine the particle charge is measuring ‘shot noise’. It is after Schottky, who measured the noise in a vacuum tube in 1918 and understood that it resulted from the discrete particle-like behavior of streaming electrons. The QHE, the earliest topological state of 2D matter, with an insulating bulk and conducting edges, hosts quasiparticles with fractional charges in the FQHE regime. Indeed, charge measurement via shot noise is important for understanding the fractional topological states.
A one-dimensional ballistic chiral QHE edge mode, propagating from a Source (S) contact to a Drain (D) contact without any backscattering, carries zero shot noise. A quantum point contact (QPC) constriction is used to induce stochastic backscattering (Fig. 1), thus leading to shot noise. The modified Schottky equation for a binomial distribution, Si=2FeIt(1-t), reveals the partitioned charge e*=Fe, with F the Fano factor and t the transmission coefficient. The noise measurement is performed at low temperatures – thus suppressing the thermal noise, and at a high enough frequency where the 1/f noise is negligible.
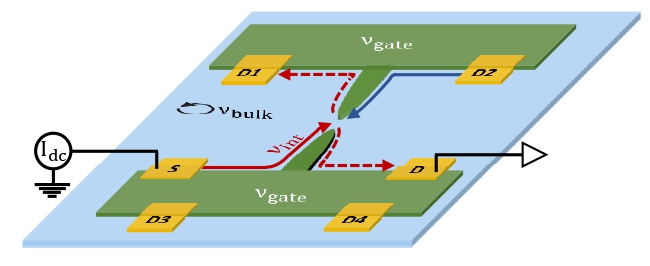
Figure 1: Shot noise measurement set up with interface edge mode. The edge mode emanates from the Source (S) contact and gets partitioned at the QPC. The noise is measured at the Drain (D) contact. For more technical details, we refer to the paper.
Using this scheme in the FQHE, e.g., at filling factor ν=1/3 and ν=2/5, past shot noise measurements yielded charges e/3 (or F=1/3) and e/5 (or F=1/5), respectively, at a relatively moderate temperature of ∼80mK. The results proved the existence of fractional charge as predicted by Laughlins’ theory of FQHE and boosted the interest in measuring the charge supported by other fractional states. Surprises showed up later. With the development of cryogenic technology, at sufficiently low temperatures (∼10mK), the shot noise at ν=2/5 and ν=3/7 led to Fano factors ≈2/5 and ≈3/7, respectively, namely, the value of the bulk filling factor. Interestingly, unexpected shot noise with F≅ν was also observed on the intermediate conductance plateaus in a partly pinched QPC constriction (where charge partitioning is not expected) at specific filling fractions, such as was also seen when reconstructed edge modes of certain filling fractions, 2/3, 3/5, and 1. This low-temperature behavior is in contradiction to the traditional understanding of shot noise caused by particles' partitioning.
To check the robustness of F = filling factor of the bulk, we came up with a new platform where the edge modes are replaced by 'engineered edge modes' at the interface between the main bulk and another bulk with a different filling factor. The interface edge 'filling', νint, is then given by the difference between the fillings of the main bulk νbulk (determined by the magnetic field) and the adjacent bulk νgate (determined by a biased gate), i.e., νint=νbulk-νgate (Fig. 1). This configuration breaks the ‘bulk-edge’ correspondence since the edge mode now belongs to two interfaced bulk regions. This architecture has the advantage of setting bulk filling and mode filling independently. We performed experiments that measured the noise of partitioned interface modes νint at a particular νbulk. In this scheme, we measured the noise of partitioned interface modes: νint=1/3, 2/3, 2/5, etc., at νbulk=1, 2/3, etc. We found that the Fano factor always follows the bulk filling factor, i.e., F≅νbulk, irrespective of the filling of the interface modes. One can notice that the measured noise has an extra contribution to that of ubiquitous Schottky noise.
How can we explain the results? We initially focused on the unexpected noise found on the intermediate plateaus within the QPC constriction, where charge partitioning is unexpected. Indeed, the observed noise on the plateaus must arise from emergent neutral modes. These modes counter-propagate to the charge modes and carry only energy. For particle-hole conjugate states, 1>ν>1/2, the neutral modes are ‘topological’ (must exist). However, spontaneous edge reconstruction leads to the proliferation of neutral modes in many states in the lowest spinless landau level. The edge reconstruction modifies the edge structure but does not alter the topological order (quantum nature) of the quantum state, i.e., the Hall conductance σxy=νe2/h and the thermal Hall conductance κxy remain conserved. For example, at ν=1, instead of only one charge mode νe=1, the reconstruction can lead to two charge modes, such as 1/3 and 1-1/3=2/3, with σxy unchanged. On the other hand, to conserve the topological κxy=1, the two fractional charge modes must be accompanied by a counter-propagating neutral mode. Note that each charge (neutral) mode contributes one positive (one negative) unit of the fundamental constant κ0 (=π2kB2/3h) to the topological thermal conductance κxy.
The excitation of the neutral modes leads to fluctuating ‘neutralons – anti-neutralons’ pairs (positive and negative neutral excitations). Subsequently, these fluctuating entities decay into random charge pulses that are added to the charge modes. Thus, the charge modes carry a fluctuating current even if there is no charge partitioning (on a QPC conductance plateau). In this process, our calculation predicts that the Fano factor of the 'total noise' is now equal to the bulk filling factor.
We then extended this mechanism to a more general case, considering: i) an edge mode gets partitioned and produces the conventional noise; ii) a neutral mode is present (as above); iii) an arbitrary edge-reconstruction with an emerging edge filling 1/m (and not a quantized fractional filling). The charge-neutral-charge mechanism explains the unexpected Fano factor being equal to the bulk filling and not to the charge of the quasiparticles.
What happens at high temperatures? It was previously shown both theoretically and experimentally that the neutral mode decays as the temperature is raised. Therefore, at reasonably high temperatures (typically above ∼30mK), the contribution of the neutral mode diminishes leaving only the 'conventional partitioning' contributing to the shot noise. Thus, at high enough temperatures, the shot noise Fano factor provides the quasiparticle charge.
Follow the Topic
-
Nature Physics

This journal publishes papers of the highest quality and significance in all areas of physics, pure and applied.




Please sign in or register for FREE
If you are a registered user on Research Communities by Springer Nature, please sign in