What should we do when the system we wish to understand has never been encountered before, and only a few, scattered observations are available?

It’s a scenario that crops up in many fields: a biologist tracking an elusive animal in the wild, a medical researcher monitoring a patient who can only come to the clinic a few times, and an environmental scientist with a faulty sensor in a remote location. In all these cases, the data are sparse, i.e., not just incomplete, but missing in irregular and unpredictable ways.

In these situations, machine learning can help. But here’s the catch: most machine learning methods require lots of training data from the system of your interest. Without that, they can’t “learn” the dynamical rules of the system. We asked this question: Could we design a machine-learning based approach that learns from other systems, then applies that knowledge to reconstruct the dynamics of a completely new, unseen system from sparse measurements alone?

The challenge of sparse and random data

When referring to “complete” data, it often means data collected at regular intervals that satisfy the Nyquist criterion, which is the golden standard for capturing sufficient information in a signal. Sparse, random data violate the standard in two ways: (1) the data points are scattered in time, without any predictable pattern and (2) more points are missing than observed.

In chaotic systems (those exquisitely sensitive to small changes), these gaps can be fatal to reconstruction. Imagine trying to guess the path of a rollercoaster if you only saw six points along the track. For certain stretches, there are infinitely many ways to connect the dots.

From frustration to a hybrid solution

We knew that directly training a machine-learning model on sparse observations of the target system wouldn’t work, as those observations might be all we ever have. So, we flipped the usual process:

1. Train a model entirely on synthetic data from dozens of well-known chaotic systems (but not the target one).
2. Give that trained model the sparse observations from the new system, and let it reconstruct the smooth and continuous trajectory.
3. Feed the reconstructed time series into a second machine-learning model to predict the long-term dynamics.

For Step 1 and 2, we chose transformer, an architecture widely used in natural language processing, due to its ability to capture long-range dependencies and adapt to sequences of varying lengths. During training, we randomized the choice of system, sequence length, and sparsity level at every step. This “triple randomness” kept the transformer from memorizing any one system and forced it to learn the general rules of chaotic dynamics of a variety of systems.

For Step 3, we used reservoir computing, which has a track record of predicting the long-term behavior of chaotic systems once it sees enough good-quality data.

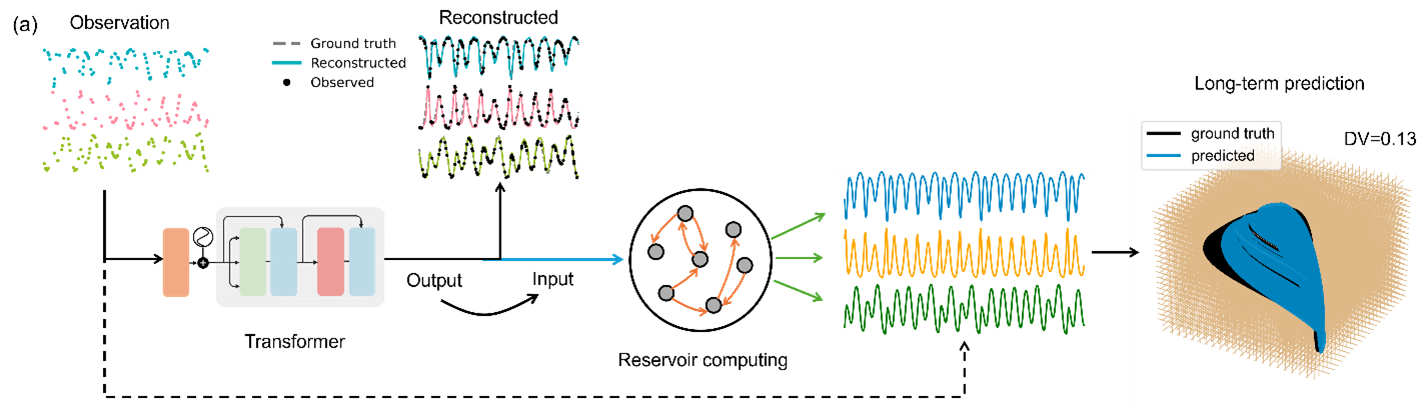
Hybrid transformer and reservoir computing framework for dynamics reconstruction. The time series reconstructed by the transformer is used to train the reservoir computer that generates time series of the target system of arbitrary length, leading to a reconstructed attractor that agrees with the ground truth.

To test the framework, we chose three target systems: a chaotic three-species food-chain model, the classical Lorenz system, and the Lotka-Volterra system.

Take the food-chain system as an example. We trained our hybrid machine-learning framework to reconstruct a time series where only about 14% of the points were given, scattered randomly. A human looking at those points wouldn’t even be able to guess the basic oscillations. Yet, the transformer filled in the gaps, capturing the correct up-and-down rhythms of each species’ population.

Why not just interpolate?

Linear or spline interpolation works fine when a small fraction of data is missing. But at high sparsity, these methods fail. They simply connect points without understanding the underlying dynamics. In contrast, our machine-learning framework learns from its synthetic training to infer how chaotic systems evolve. Our framework performs better than compressed sensing and other machine learning models.

Why does this matter?

The hybrid framework offers a way to study systems that were previously “off limits” to machine learning: (1) no training data from the target system required, (2) works under extreme data sparsity, and (3) capable of generalizing to unseen systems.

Potential applications span ecology, climate science, medicine, and engineering, i.e., anywhere critical decisions depend on making sense of incomplete, irregular measurements. For example, wearable health monitors often miss large chunks of data when batteries die, or when devices are removed. Our approach could reconstruct continuous vital-sign time series from those fragments, enabling early warnings for health events.

Looking ahead

One of the most exciting aspects of this work is the hint that it could be developed into a foundation model for dynamical systems. In our computational experiments, reconstruction error followed a power-law trend as we increased the diversity of training systems, suggesting that with enough variety, the model might generalize to almost anything in its class.

The road ahead includes tackling nonautonomous systems, refining our understanding of the theoretical limits of the reconstruction paradigm, and testing in real-world data scenarios.

What began as a frustration (that we could not train on the system we wanted to study) has turned into a method that thrives on that very challenge. Sometimes, the best way to learn about something new is to learn from everything else.