Controlling dislocation motion using an electric field
Published in Materials
Manipulating dislocation motion has been a longstanding interest in materials research. The movement of dislocations is crucial for both fundamental science and applications of crystalline materials, such as the plastic deformation, phase transition, and amorphization of crystals1, 2, 3. Since the introduction of the dislocation theory in the 1930s, the movement of dislocations has been commonly attributed to mechanical stress, and related dislocation dynamics have been well studied in theory and experiment1. For example, it is known that dislocation motion under stress can be influenced by temperature, electrical pulses and illumination4, 5. Since stress-driven dislocation is the cornerstone of the classical dislocation theory, controlling dislocation motion solely by a non-mechanical stimulus is less expected. Dislocation dynamics under a non-mechanical stimulus alone is an almost virgin field due to the lack of direct experimental evidence.
Although the dislocation motion under a non-mechanical stimulus does not draw much attention, there have been some studies on this topic. Early experiments examining the interaction between dislocations and electric fields can be dated back to the 1960s6, 7. In the alkali halide samples in a high electric field (~106 V m-1 or 7.5 kV), the positions of etching pits on the surface of these samples changed after applying this field. These preliminary results suggest possible interactions between dislocations and electric fields. However, there is no direct evidence on the controlled dislocation motion by an electric field.
The development of in situ transmission electron microscopy (TEM) techniques provides us an opportunity to reveal the dislocation dynamics under external stimuli8. TEM has been widely used to study dislocations since the 1950s9. Its high spatial resolution can distinguish single dislocations at the nanometer scale. The in situ TEM electrical testing system enable to apply electric fields on samples while recording the response of dislocations in real-time.
In our article (https://www.nature.com/articles/s41563-023-01572-7
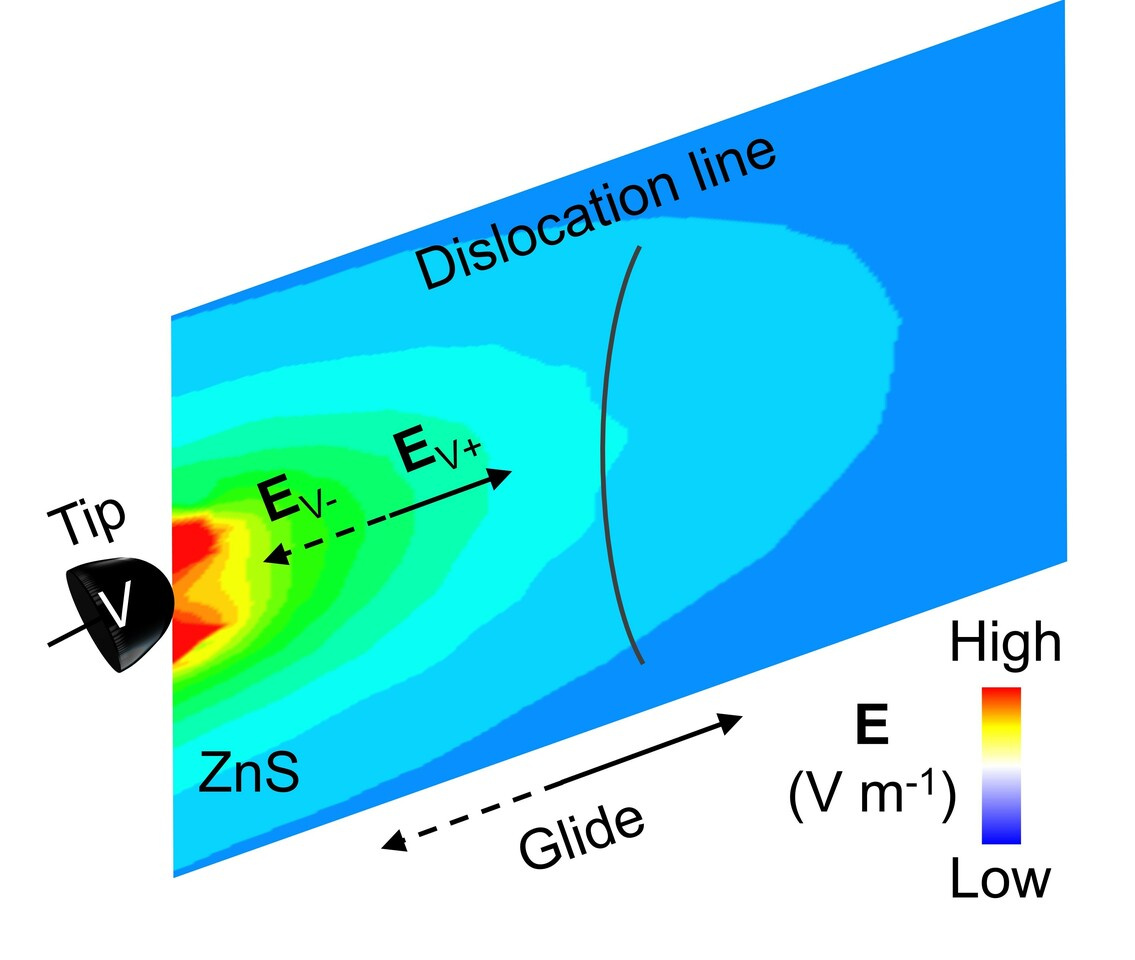
https://rdcu.be/deSTA), we investigated the dislocation behavior under an electric field in ZnS using in situ TEM electrical testing system. Video 1 shows the recorded dislocation response under an applied voltage by a metal (W) tip. We find the dislocation moves back and forth depending on the magnitude and direction of external electric fields in the absence of mechanical loading. The dislocation behaves like a charged line in an electric field. For example, when the applied electric field is positive, the dislocation moves away from the tip. When the applied voltage is negative, the dislocation moves back to the tip. The maximum velocity on the dislocation line is ~306.4 nm s-1. This result provides direct evidence of the electric-field control of dislocation motion.

Video 1. In situ TEM observation of an individual dislocation moved in an external electric field. The dislocation moves back and forth depending on the magnitude and direction of the electric field.
We compared the mobility of different dislocations under an electric field, such as 30° and 90° partial dislocations. We found a sample with alternatively arranged 30° and 90° partial dislocations, providing an ideal platform to compare their mobility. Then we carried out electrical testing in this region. Video 2 shows that 30° partial dislocations move back and forth depending on the direction of the electric field, while 90° partial dislocations are motionless. Therefore, 30° partial dislocations are more mobile than 90° partial dislocations under electric fields. Furthermore, the motion features under electric fields can be clearly observed in Video 2, such as the pinning-depinning process and kink propagation. This comparison improved our understanding of dislocation motion under an electric field.

Video 2. The comparison of 30° and 90° partial dislocations in an electric field. The 30° partial dislocations (Dislocations B and D) move back and forth, driven by the applied electric field while the 90° partial dislocations (Dislocations A, C, and E) are motionless during the whole experiment.
To understand how an electric field drives dislocation motion, we characterized the atomic structure of dislocations by direct imaging, and electronic structure by theoretical calculations. Fig. 1a shows atomically resolved images of a dislocation. The brighter and larger spots indicate Zn columns while the smaller spots indicate S columns. Therefore, we can determine it is a 30° S dislocation in this image. Theoretical calculations based on the atomic structure show that the negatively charged 30° S core is more stable compared with the neutral state. The blue cloud in Fig. 1b represents the additional electrons (e-) localized around the 30° S dislocation. The charged nature of the dislocations enables the manipulation of the dislocation motion using an electric field through Coulomb interaction. Fig. 1c shows that the glide barriers of the charged dislocation tend to decrease under electric fields. We also analyzed other three types of dislocations with the same method where all glide barriers show a decreasing trend under electric fields. The decreased glide barrier elucidates the mechanisms of electric-field-controlled dislocation motion from an energetic perspective.
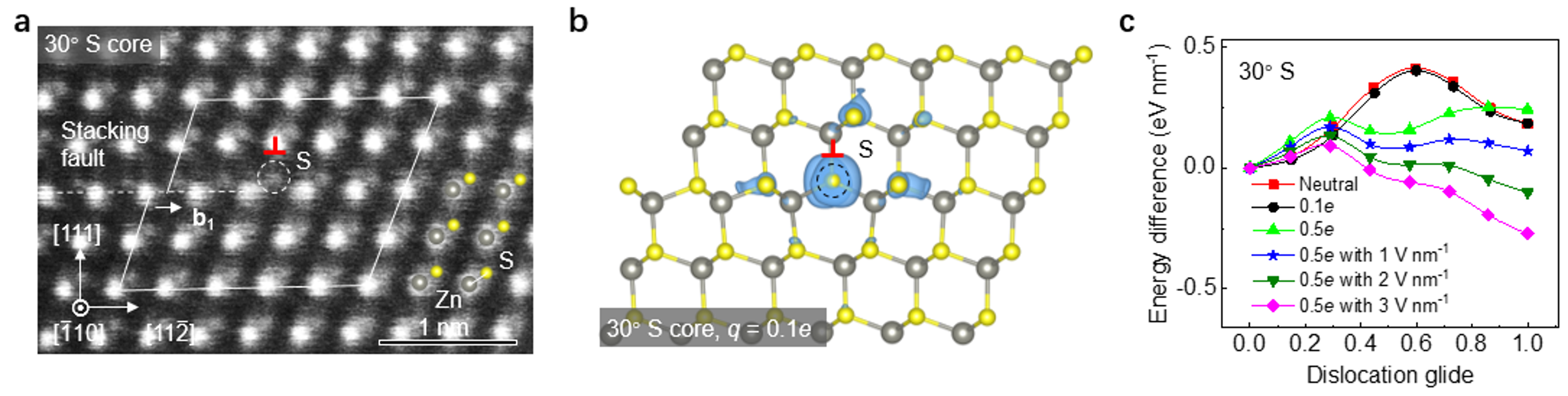
Fig. 1. Atomic structures and glide barrier of 30° partial dislocations in ZnS. (a) Atomically resolved images of a 30° S dislocation. (b) The net charge distributions of the 0.1e- charged 30° S dislocation. (c) The influence of charge states and electric field on glide barriers of a 30° S dislocation.
This work provides not only direct evidence for dislocation dynamics under an electric field but also new possibilities for manipulating dislocation-related properties, such as mechanical performance and formability of brittle crystalline materials. However, the dislocation dynamics under non-mechanical stimuli is far from being fully understood compared with the dislocations under mechanical stress. We hope our work can provide a reference for future studies.
References
- Hull D, Bacon DJ. Introduction to dislocations, vol. 37. Elsevier, 2011.
- Nam S-W, Chung H-S, Lo YC, Qi L, Li J, Lu Y, et al. Electrical wind force–driven and dislocation-templated amorphization in phase-change nanowires. Science 2012, 336(6088): 1561-1566.
- Reddy KM, Guo D, Song S, Cheng C, Han J, Wang X, et al. Dislocation-mediated shear amorphization in boron carbide. Sci. Adv .2021, 7(8): eabc6714.
- Troitskii O, Likhtman V. Anisotropy of the effect of electronic and α-irradiation on the process of deformation of zinc single crystals in the brittle state. Dokl. Akad. Nauk SSSR; 1963; 1963. p. 332-334.
- Osip'yan YA, Petrenko VF, Zaretskiĭ AV, Whitworth RW. Properties of II–VI semiconductors associated with moving dislocations. Adv. Phys. 1986, 35(2): 115-188.
- Mendel E, Weinig S. Generation of Dislocations by an Electric Field in MgO. J. Appl. Phys. 1960, 31(4): 738-739.
- Caffyn J, Goodfellow T, Hamdani A. The movement of dislocations in an electric field in sodium chloride. Mater. Res. Bull. 1967, 2(12): 1067-1073.
- Zheng H, Meng YS, Zhu Y. Frontiers ofin situelectron microscopy. MRS Bull. 2015, 40(1): 12-18.
- Berghezan A, Fourdeux A. Transmission electron microscopy studies of the mechanism of plastic deformation. J. Appl. Phys. 1959, 30(12): 1913-1922.
Follow the Topic
-
Nature Materials

A monthly multi-disciplinary journal that brings together cutting-edge research across the entire spectrum of materials science and engineering, including applied and fundamental aspects of the synthesis/processing, structure/composition, properties and performance of materials.



Please sign in or register for FREE
If you are a registered user on Research Communities by Springer Nature, please sign in