Dynamical transition in controllable quantum neural networks with large depth
Published in Physics and Computational Sciences

Introduction
Quantum neural networks (QNNs), a paradigm for near-term quantum computing, have been widely applied in fields such as chemistry, optimization, quantum simulation, condensed matter physics, sensing and machine learning. However, the fundamental study of late-time QNN training dynamics remains largely unexplored. Previous results, such as the barren plateau and Quantum Neural Tangent Kernel (QNTK) theory, focus on QNNs at random initialization and fails to capture the quantum circuit towards late-time convergence. Can we open this black box by providing a theoretical understanding of QNN training dynamics at later stages?
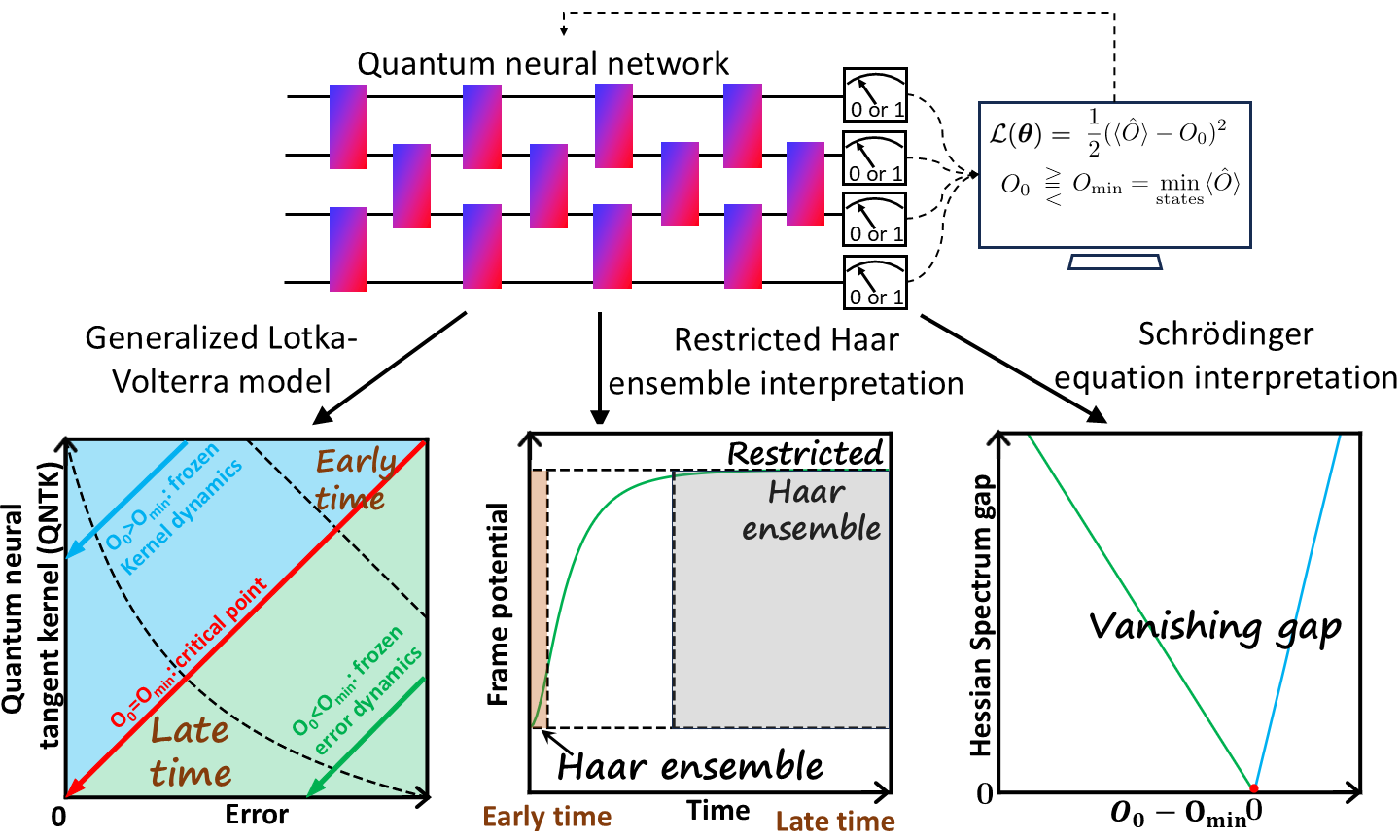
Dynamical transition in training dynamics
The training of the QNN aims at minimizing the cost function, for instance, the squared error between measurement expectation of output state and the target value (Fig.1). At each training step, every parameter in the quantum circuit is updated using gradient descent. Through the first-order Taylor expansion, we derive the generalized Lotka-Volterra equation to describe the training dynamics of error and QNTK simultaneously where the QNTK is the squared norm of the gradient. Interestingly, the generalized Lotka-Volterra equation here parallels the predator-prey dynamics in environmental biology, with a zero birth rate. Identifying a conserved quantity from the dynamical equation, we can obtain the analytical solutions for two branches of dynamics and a critical point, summarized in Fig.1 left corner. When the target is greater than the minimum eigenvalue of measurement operator, the error decays exponentially while the QNTK remains constant, leading to the frozen-kernel dynamics. For target value equals the minimum eigenvalue, both error and QNTK decays polynomially with training steps, leading to the critical point. When the target value is set below the minimum eigenvalue, the total error converges to a nonzero constant due to unachievable target corresponding to the frozen-error dynamics, however, the vanishing part of error and QNTK will decay exponentially. This dynamical transition corresponds to a transcritical bifurcation, where stability exchanges occur between fixed points.
Speedup the convergence
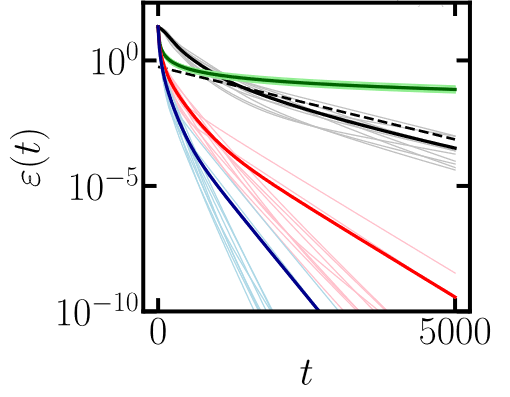
Our theoretical framework can also be applied to the training dynamics of linear loss, which decays exponentially toward ground state energy at a fixed rate. In quadratic loss, setting the target value at the ground state energy can only enable a polynomial decay of error, which is much slower than the ground state preparation with linear loss. However, setting the target value below the ground state energy allows exponential convergence toward the ground state, with the rate of convergence controlled by the target, resulting in faster convergence. We compare the decay of errors of these cases in Fig.2, and verify the speedup with theory predictions.
Discussion
Our results go beyond early-time assumptions based on random initialization in QNN studies, uncovering rich physical insights from the training dynamics. The target-driven transcritical bifurcation transition in the dynamics of QNN suggests a different source to the transition without symmetry breaking and provides guide on better design of cost functions in practical applications. Our work can also be viewed as a single-data scenario in supervised learning, paving the way for a theory of data in quantum machine learning.
Follow the Topic
-
Nature Communications

An open access, multidisciplinary journal dedicated to publishing high-quality research in all areas of the biological, health, physical, chemical and Earth sciences.
Ask the Editor – Space Physics, Quantum Physics, Atomic, Molecular and Chemical Physics
Got a question for the editor about Space Physics, Quantum Physics, Atomic, Molecular and Chemical Physics? Ask it here!
Continue reading announcementRelated Collections
With Collections, you can get published faster and increase your visibility.
Clinical trials 2025
Publishing Model: Open Access
Deadline: Dec 31, 2025
Women's Health
Publishing Model: Hybrid
Deadline: Ongoing




Please sign in or register for FREE
If you are a registered user on Research Communities by Springer Nature, please sign in