Many evolving communities depend on public goods that are contributed by some at a cost, but benefit all. The evolutionary stability of cooperation in the public goods game (PGG) is vulnerable to the tragedy of the commons, or free-rider problem. Work in 2015 demonstrated a non-linear relationship between the number of cooperators and the games’s benefit (to fitness) in a cancer cell line. As a result, cooperators and free-riders can coexist. In many systems it is important to ask when such coexistence is stable, “how groups of individuals form and how they arrive at decisions that ultimately benefit all”, or how microbial communities maintain coexistence.

After the cancer cell line results were published, my colleague Philip Gerlee and I felt that two things were still missing. First, the initial mathematical description qualitatively captured the non-linear nature of the cancer cell-public goods game but described payoffs and fitness rather than births and deaths of cells, potentially dismissing population growth. Second, the data (Fig. 1) was not used explicitly to describe net growth rates, possibly because the fitness function of the evolutionary game could be difficult to parameterize. However, we like the PGG in co-evolving cell populations because it can be more than a heuristic. As a result, one might be able to directly tie empirically observed population dynamics to growth factor dynamics and cell cycle dynamics, which Philip and I had modeled before using in vivo growth data and a PGG in linear form. 

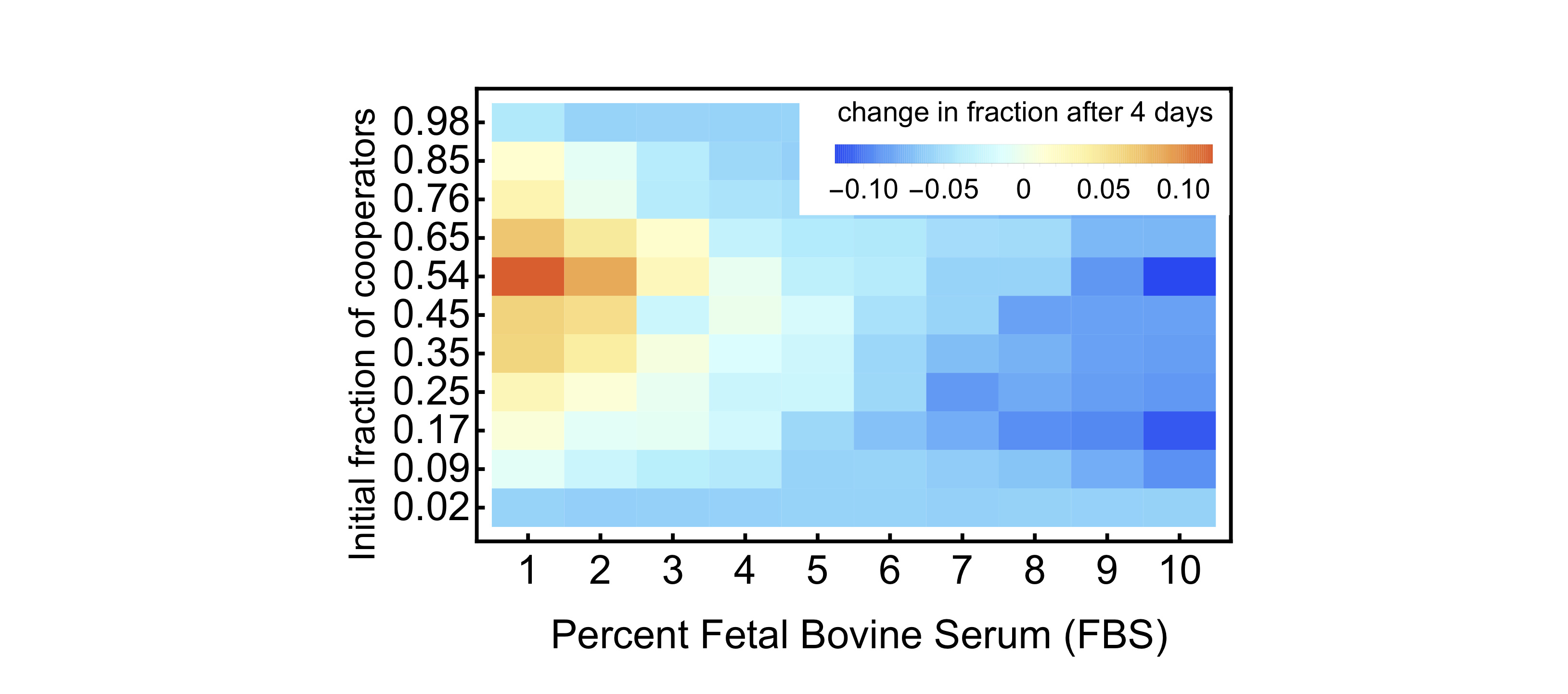
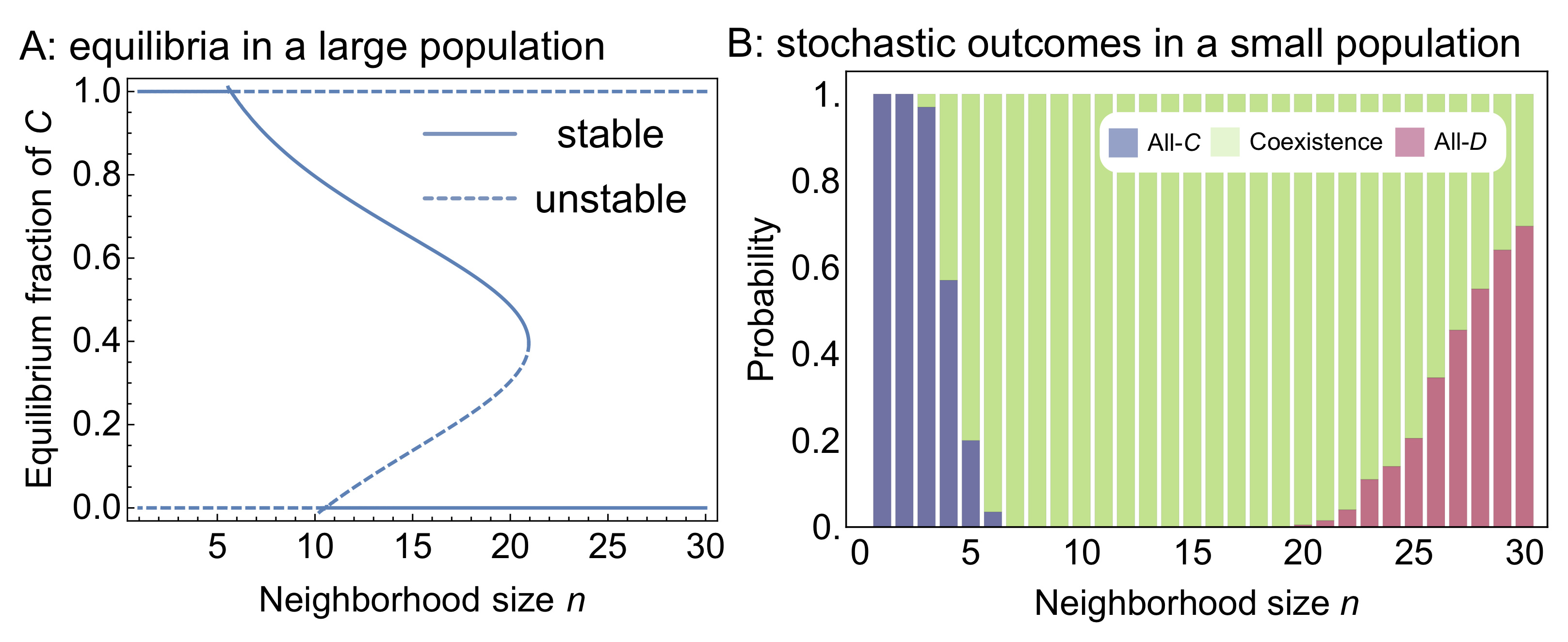
 Since we knew that interesting PGGs are non-linear, Philip Gerlee, Gregory Kimmel, Joel Brown and I began to look into possible mechanisms that can explain coexistence and multiple stable equilibria in this complex system. It was also important to us to link our model to the data from 2015. We started with the idea that the non-linear public good acts in a finite neighborhood, and that its growth rate function steeply increases at first but saturates with a sufficient number of cooperators. We modeled the population game either as a deterministic system, or as a stochastic process, which means that we can predict the number of evolutionary stable states in large populations (deterministic), or the probability of cooperation-extinction in small populations (stochastic). The neighborhood critically determines these states and probabilities (Fig. 2), and the system could explain the previously measured cell line growth rates (we are grateful that Dr Marco Archetti shared the original data with us).

We are convinced that our approach is relevant to many different systems in ecology and evolution. Thus, we first sent the manuscript to Nature Ecology and Evolution, where it was desk rejected and transferred to Nature Communications. There, it was editorially reviewed, rejected because of research parasitism (we indeed used previously published, i.e. 'old', data), and forwarded to Communications Biology, where we experienced a very constructive peer review process that helped to improve our methods and solidify our results. The referees’ comments triggered us to think deeper about of how the public good’s neighborhood size emerges statistically and how to calculate growth rate functions. 

We are particularly excited about future work in which neighborhood size itself is under selection, hence asking whether and how populations evolve traits that determine the number of peers with which they can interact, and how this impacts the population's ability to adapt.