
The global ocean circulation comprises flow features that range from a few thousand km of large ocean gyre structures to small micrometer flows. The complexity in the ocean flow structure arises through several physical processes such as atmospheric winds, ocean turbulence, wave breaking, and ocean flow interactions with bathymetry. These multi-scale ocean flows and how they couple with each other are crucial for regulating Earth's climate and ecosystem, as ocean currents transport heat, carbon, and nutrients around the globe. Hence, it is useful to diagnose the energy of oceanic flows at different length scales to evaluate the impacts of ocean turbulence on the global ocean circulation and the earth system.
With the advent of satellite observations and high-resolution ocean models, it is now possible to observe ocean flow features and analyze how these turbulent oceanic flows of different length scales interact. The most common way to perform such analyses is to compute the Fourier transform of velocity field to obtain kinetic energy spectrum, which basically measures the energy intensity, as a function of wavenumber (or inverse of length scale). The kinetic energy spectrum is very effective in identifying the size of most energetic flow structures, sources, and sinks of energy at different length scales; thus, estimating how significant these flows could be for the global ocean circulation.
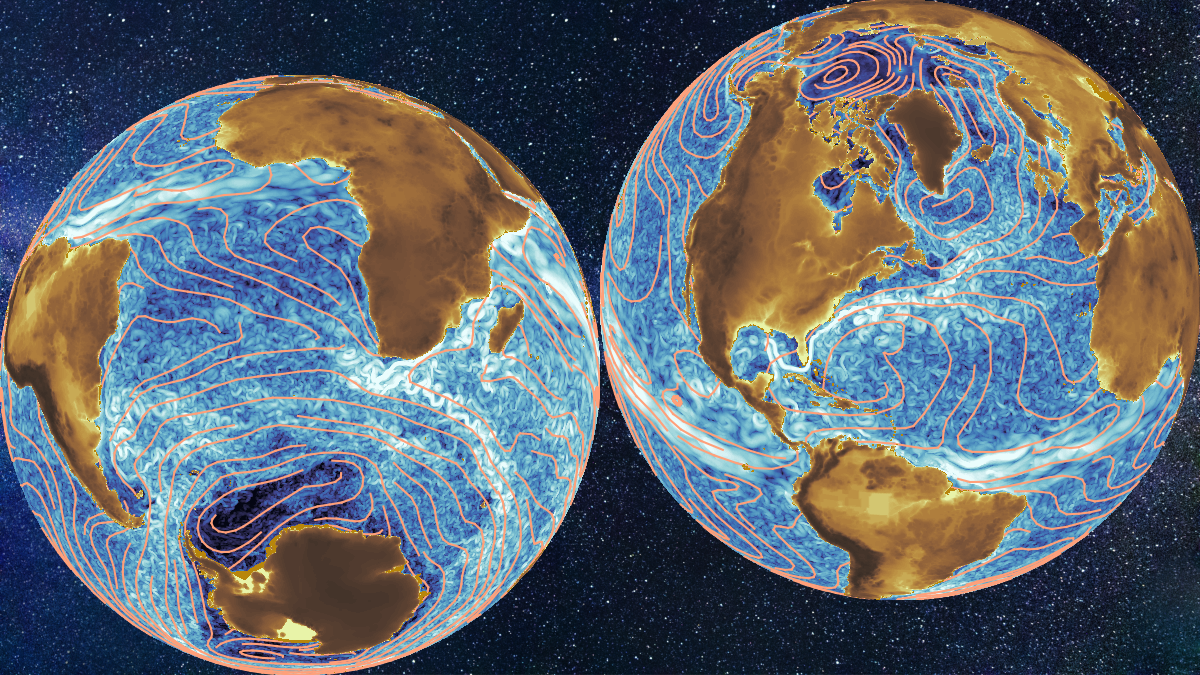
Previous analyses have shown that oceanic mesoscale eddies, which are typically about 100-500 km in diameter, form the peak of the kinetic energy spectra and contain most of the kinetic energy in the oceans. Moreover, a kinetic energy spectrum can inform us about the physics of underlying turbulent processes. For example, mesoscale kinetic energy spectra in the oceans generally follow a k-3 power law, which is associated with a forward enstrophy cascade as predicted in the theory of two-dimensional turbulence. However, Fourier transform requires a signal to be periodic and spatially homogeneous. Since these conditions are not valid at planetary length scales due to the presence of continents, most of the spectral analyses in the oceans are carried out in small regions that are typically 1000 km wide and are away from the continental boundaries. Consequently, Fourier spectra cannot determine the energy distribution at planetary length scales in the oceans.
In our study, we employ a novel approach called the "Coarse-Graining method", which does not suffer from the limitations of the Fourier transform, to compute the kinetic spectrum of the global ocean circulation using satellite observations and high-resolution ocean model outputs. The results show that the global kinetic energy spectrum truly peaks at about 10000 km and 4000 km due to the Atlantic Circumpolar Current and ocean gyres. In addition, the global kinetic energy spectrum reveals a k-1 power law at length scales longer than 1000 km, which was not observed in any previous research. A complete theoretical understanding of this newly discovered power law scaling is missing; nevertheless, previous research works have suggested that the k-1 power law could be due to the action of winds on the ocean surface. Our analysis further shows that the relative kinetic energy contributions at different length scales vary highly with the season – mesoscale flows tend to be strongest in late spring, whereas gyre-scale flows peak in early winter. Hence, cross-scale turbulent interactions and the resulting energy exchange are important for understanding ocean variability.
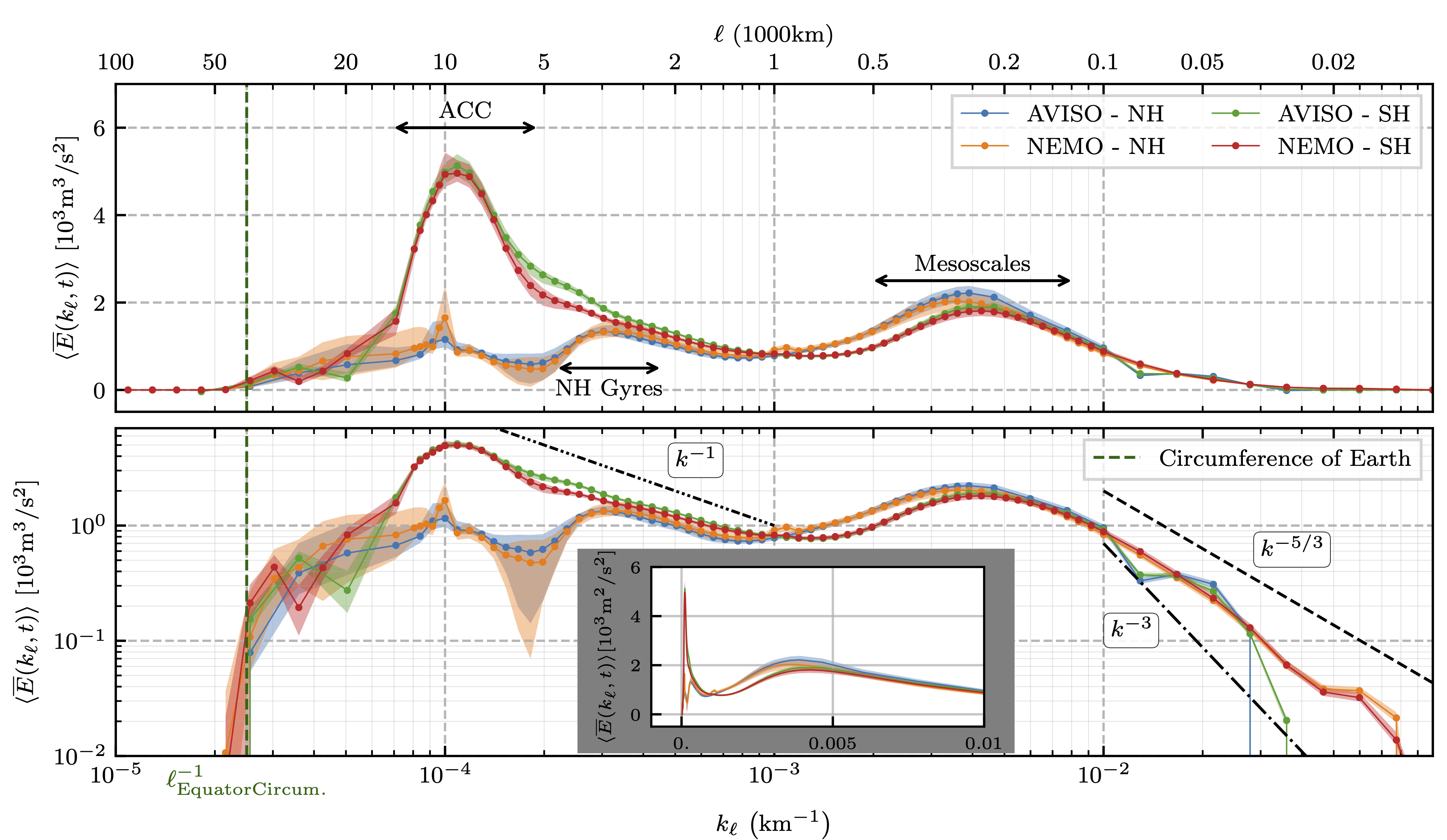
These results will not only help us better understand the dynamical coupling between gyre-scale flows and relatively small mesoscale flows in the oceans but also present a novel method to perform scale-dependent analysis in a variety of scenarios. For example, by decomposing a signal as a function of length scale, one can assess the impact of small-scale turbulence, which is difficult to resolve in current climate models, on ocean circulation. We hope that the new methodology and results will generate innovative ideas to study physical processes in the oceans and contribute to improving ocean models.
Follow the Topic
-
Nature Communications

An open access, multidisciplinary journal dedicated to publishing high-quality research in all areas of the biological, health, physical, chemical and Earth sciences.
Related Collections
With Collections, you can get published faster and increase your visibility.
Women's Health
Publishing Model: Hybrid
Deadline: Ongoing
Advances in neurodegenerative diseases
Publishing Model: Hybrid
Deadline: Mar 24, 2026


Please sign in or register for FREE
If you are a registered user on Research Communities by Springer Nature, please sign in