How large macromolecules move in a crowded environment?
Published in Chemistry

The paper in Nature Communications can be found here:https://www.nature.com/articles/s41467-018-04661-3
Polymers are usually diffusive no matter in solutions or under confinement. Even under strong confinement (reptation model), they still move forward like a snake! So how to make polymers calm down and hibernate? One possible way is by lowering the temperature, where polymers become glassy and lose their ability to move. Here we think of another way: topological frustration! Compared to the low-temperature frozen polymers, in topologically frustrated state, polymers stay awake but still cannot diffuse.
In our work, very long and concentrated charged polymers live in a charged hydrogel. Their motions are monitored by a detector on a light scattering instrument. The gel mesh size is much smaller than the chain size, but much larger than the chain segment length. Surprisingly, we found the center of mass of the chains does not diffuse inside the hydrogel. But the hydrogel contains 96% water! How can the polymer chains stand still to fall asleep instead of swimming happily in such a big swimming pool? The truth is that the segments inside each mesh undergo considerable conformational fluctuations and swim locally, experiencing Rouse or Zimm dynamics. But since one chain occupies around 34 gel meshes in three dimensions and each mesh functions as an entropic trap, so if the whole chain wants to move, the segments in all the 34 meshes must do the teamwork to move simultaneously to overcome all the entropic barriers between the traps (meshes). But unfortunately, they don’t have a team leader (such as an externally applied electric field) to work effectively so that the center of the mass of the whole chain is essentially localized in the experimental time scale. This state is defined as topologically frustrated localization. However, by lowering the polymer molecular weight or polymer concentration in the hydrogel, part of the polymers will be released from these entropic traps and become diffusive. Both theory and experiments prove that the monomer density correlation function for this topologically frustrated state obeys the stretched exponential law with the stretched exponent β in a very narrow range 1/3 < β <2/5, instead of the full range 0 < β < 1 seen in traditional glassy and aging systems.
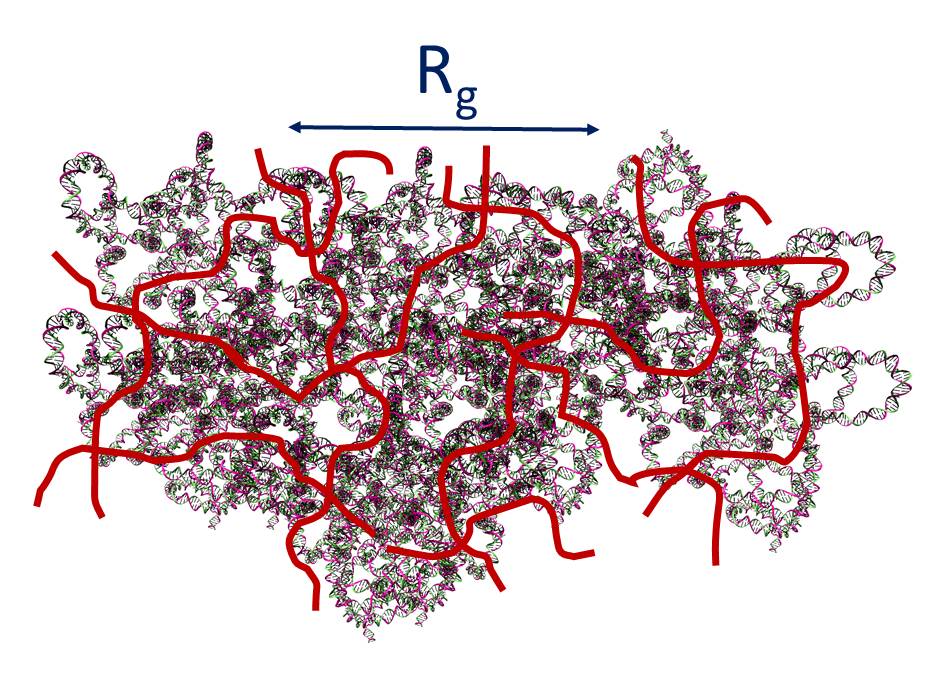
Our work opens a new angle to realize thermally driven glassy behavior by temperature-independent topologically frustrated localization, which is important for human body. For example, can we control the DNA motion in a crowded tissue at room temperature? Can we deliver some charged macromolecules to the specific organ and release them in a crowed media?
Of course, there are still questions: What is the lifetime of the topologically frustrated state? What will happen if an electric field is applied? If heating the system, can the extra energy help to overcome the entropic barriers and destroy the topologically frustrated localization? Or even can all the segments of one chain do the teamwork and move simultaneously under the guidance of a magic leader? The answers are on the way……..



Please sign in or register for FREE
If you are a registered user on Research Communities by Springer Nature, please sign in