Imprints of Cosmological Tensions in Reconstructed Gravity
Published in Astronomy

A century after Einstein's revolutionary formulation of gravity in terms of a dynamical four dimensional space-time, we have an established standard model of cosmology, the Λ Cold Dark Matter (ΛCDM) model, based on the laws of General Relativity (GR). Over the past couple of decades, we have measured the parameters of this model with ever increasing accuracy. Yet, our understanding of the major constituents of the Universe is limited at best: only ~ 5% of it is made of components we know! The remaining energy budget is in the form of dark matter (~25%), responsible for the clustering of matter, and dark energy (DE) (~70%), believed to be responsible for cosmic acceleration (the cosmological constant in ΛCDM). We still lack compelling theoretical models for both and, yet, it could simply be that our understanding of gravity when applied to large cosmological distances is incomplete.
GR is one of the most successful physical theories, having passed many tests in Earth-based laboratories and the Solar System and, more recently, having been spectacularly validated by the direct detection of gravitational waves from binary black holes and neutron stars. None of these tests, however, probe GR on cosmological scales, were gravity, in addition to being sourced by massive objects, is characterized by the Hubble expansion of the Universe.
What can Cosmology tell us about gravity? The worldwide astronomical community has embarked on an intense observational effort to address this question. Up and coming missions will deliver a highly accurate 3D map of the clustered matter in the universe, which cosmologists call “large scale structure” (LSS), offering an unprecedented insight into gravity at large distances. In the meantime, ongoing cosmological surveys have already started to tighten constraints unveiling some possible cracks in the standard model. In fact, a few notable tensions have recently emerged between some of the datasets when interpreted within ΛCDM. Most notably, the Hubble tension referring to a 5σ disagreement between the value of the Hubble constant today, H0, predicted by the ΛCDM fit to cosmic microwave background (CMB) measurements and the most recent direct determination from Cepheid calibrated type Ia Supernovae (SNIa). Another persisting tension regards the amount of clustering, encoded in the parameter S8; the best fit to CMB predicts a Universe which is roughly 10% more clustered than what galaxy weak lensing surveys observe. Finally, the CMB temperature anisotropy measured by Planck appears to be affected by weak gravitational lensing more than what is expected in ΛCDM.
With an agnostic approach to gravity, and more generally to the cosmological model, we can encase possible modifications of ΛCDM in three phenomenological functions, describing the expansion of the Universe, Ωx, and the effects of gravity on light, ∑, and matter, µ. The observable Universe is homogeneous and isotropic on large scales, well described by the flat FLRW metric; Ωx describes the collective contribution to the expansion by anything other than radiation and matter, including a cosmological constant, dynamical DE, modifications of gravity, as well as a possible non-zero spatial curvature. It is, naturally, a function of time only. ∑ and µ characterize the inhomogeneities (or clumpiness) of the Universe, and describe the behavior of weak gravitational lensing and clustering, respectively.
We consider all three phenomenological functions and, for the first time, perform a joint Bayesian reconstruction of them from a combination of recent cosmological observations. In practice, we divide the redshift interval covered by the current data into a finite number of bins, and we assign a value to the three functions in each of these bins. Overall this results in O(30) extra parameters to fit to the data along with the six standard cosmological parameters.
Which data do we use? We consider several combinations of currently available cosmological data: CMB (temperature, polarization and reconstructed lensing) from Planck 2018, baryon acoustic oscillations (BAO) from eBOSS-DR16, the Pantheon compilation of SNIa, galaxy clustering plus weak gravitational lensing from DES Year 1 and redshift space distortion (RSD) from eBOSS.
In order to prevent unphysical features related to an over-fitting of the data, we include in the reconstruction a theory-informed prior based on the broad class of Horndeski gravity theories. The latter, introduced by Gregory Horndeski in 1974, and later rediscovered as the class of Generalized Galileon theories, provides a unifying description of extensions to ΛCDM relevant at late times.
The outcome of our reconstruction gives us the first glimpse of what gravity looks like on cosmological scales, along with a very encouraging estimate of the constraining power of current data. Namely, we find that the data can measure fifteen combined (eigen)modes of the three functions! This is significantly more than the few modes commonly fit via simplified parametrizations, and it means that current data can already tell us quite a lot about how gravity behaves over large, cosmological distances. The main results can be seen in Figure 1.
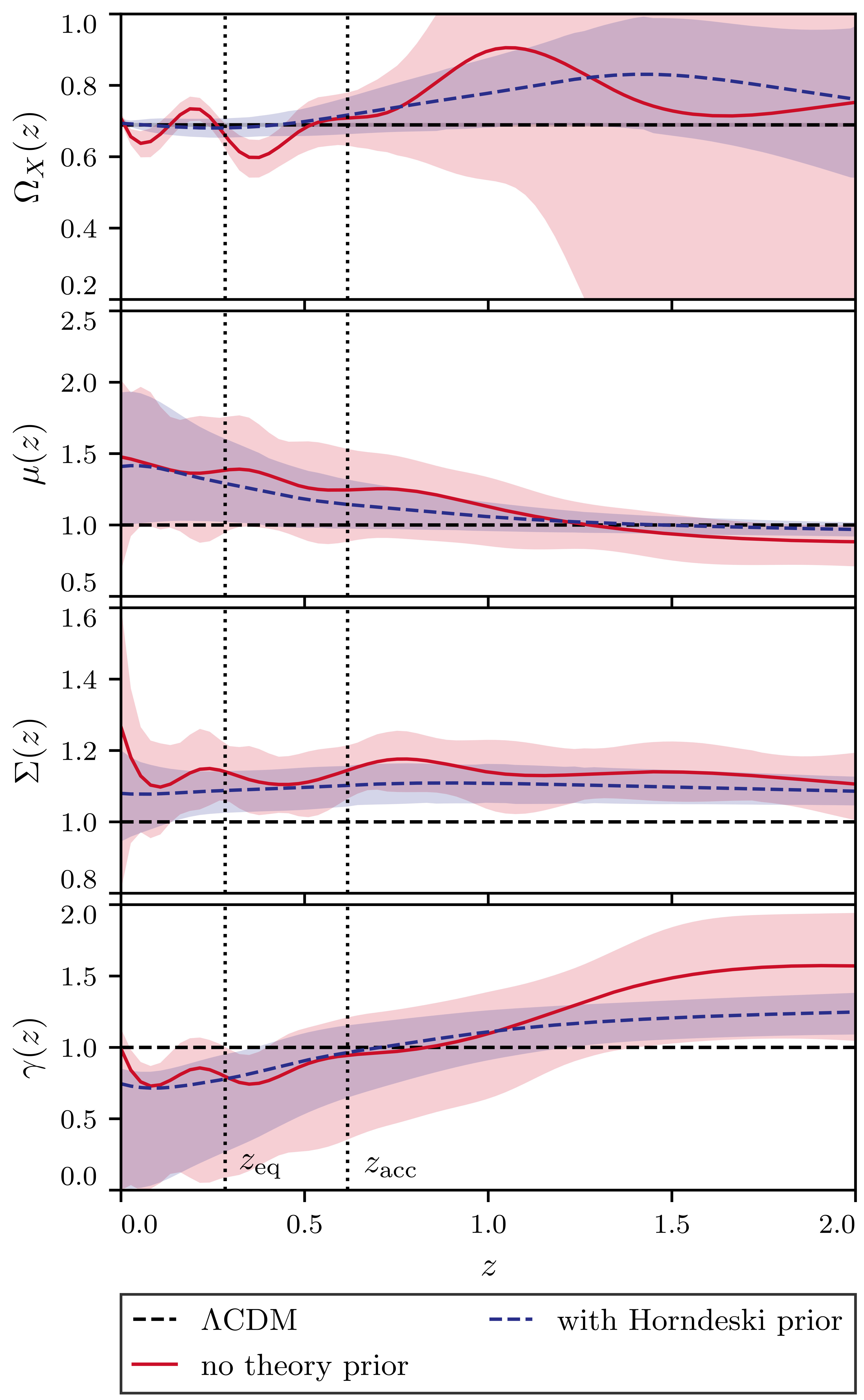
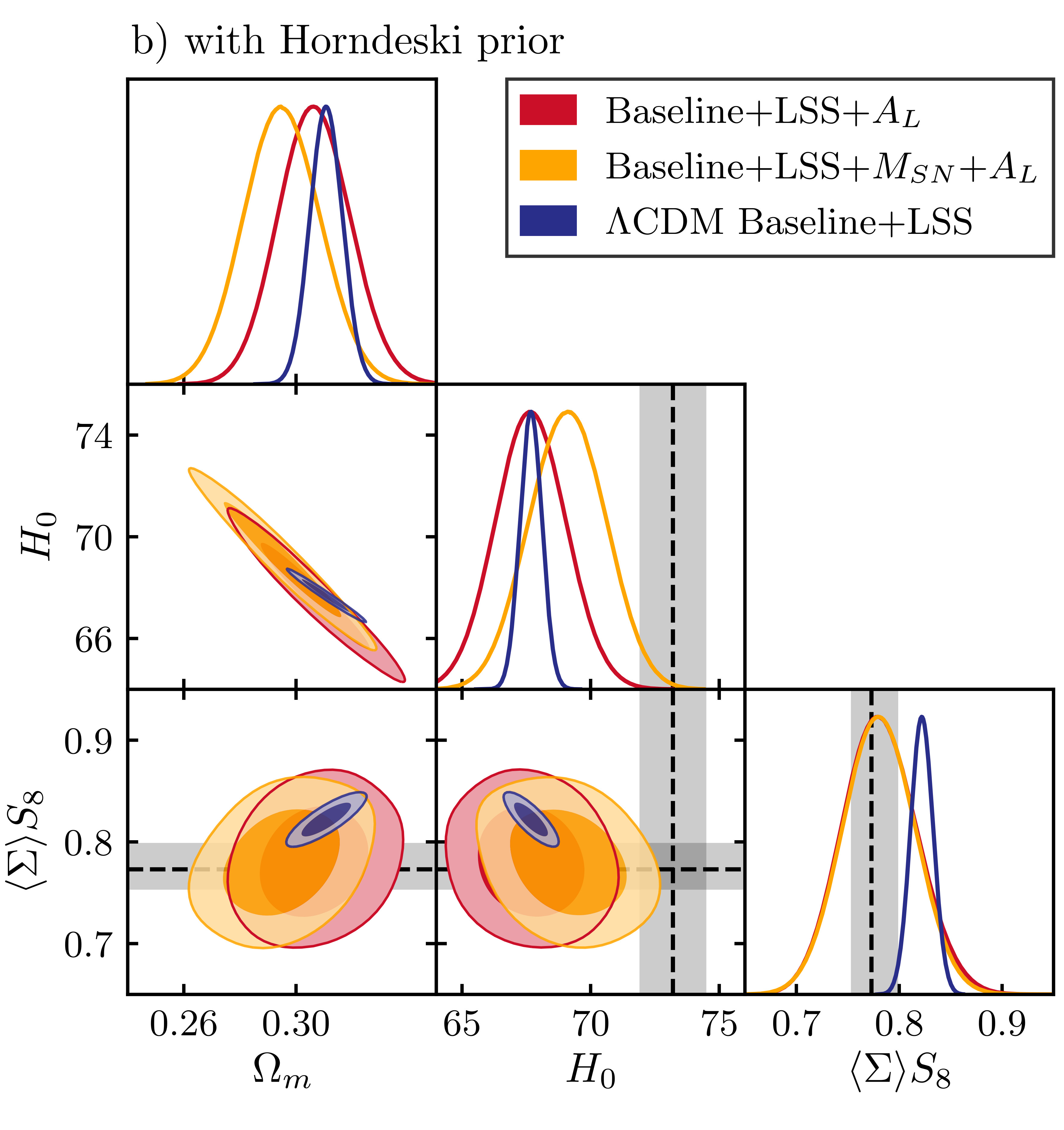
Interpreting our findings in light of the above-mentioned cosmological tensions, we can identify the phenomenological features that extended theories would need to have in order to ease some of the tensions. The function whose behaviour is most directly linked to the tensions is the lensing one, ∑, for which we find a mild (2σ) evidence of deviation from unity (i.e. its value in ΛCDM) . At earlier times, higher redshifts, that is really a reflection of the lensing anomaly in CMB. And indeed that features goes away if we introduce the AL parameter, which accounts for the lensing deficiency within Planck. However, the deviation of ∑ from unity at later times, lower redshifts, is robust and allows to significantly ease the S8 tension. The dynamical features in Ωx help with reducing the H0 tension, but not resolving it (and do so at the expense of an increased uncertainty in H0). All this can be seen in Figure 2.
In Figure 1 we also show the reconstruction of the gravitational slip gamma, derived from properly combining the reconstructed µ and ∑; this parameter measures the difference between the effective gravitational coupling strengths to matter and light and it is considered a smoking gun of modified gravity, since a deviation of it from unity would imply a violation of the equivalence principle! We find a (2σ) trend for a deviation from unity both at higher and lower redshifts, with an interesting crossing of unity somewhat in the middle of our redshift range. If confirmed at higher statistical significance, the latter feature would exclude the popular class of theories known as Generalized Brans Dicke!
In conclusion, as the era of precision cosmology is unfolding, we are on the brink of learning about gravity on cosmological scales with high precision. Current data already draw an interesting picture, which, if confirmed with higher constraining power, could pave the way to resolving some of the open challenges in Cosmology.
Follow the Topic
-
Nature Astronomy

This journal welcomes research across astronomy, astrophysics and planetary science, with the aim of fostering closer interaction between the researchers in each of these areas.
Related Collections
With Collections, you can get published faster and increase your visibility.
Progress towards the Sustainable Development Goals
Publishing Model: Hybrid
Deadline: Ongoing



Please sign in or register for FREE
If you are a registered user on Research Communities by Springer Nature, please sign in