Quantum chemistry methods are important building blocks within fields as varied as materials science, drug discovery, catalysis, and molecular biology. Common applications include the computation of quantum mechanics properties such as HOMO (highest occupied molecular orbital) and LUMO (lowest unoccupied molecular orbital) energies and the HOMO-LUMO gap, molecular dipoles, rotational constants, atomic charges, molecular potential energies and forces, and more. Recent works have also focused on providing and predicting Hamiltonian matrices for molecules. Historically, such computations have been handled with numerical solutions such as the Hartree-Fock, Post-Hartree–Fock, and Density Functional Theory (DFT) methods. However, the most accurate algorithms, such as the “gold standard” coupled-cluster (Post-Hartree–Fock) method, scale extremely poorly in terms of computational resources, with algorithmic complexities given by high-degree polynomials (such as O(n⁷)) in terms of the number of basis functions, which in turn usually depends on the number of electrons. To combat these limitations, semi-empirical methods have been proposed as an alternative to techniques based on first principles which incorporate experimental (empirical) data to estimate certain parameters that would otherwise be computationally expensive. Such methods can be orders of magnitude faster than DFT.

At the same time, data-driven methods that learn from large datasets of quantum mechanical properties have been at the forefront of machine learning research for a long time. Although such methods are considered “black boxes” and rely on large datasets and the ability of models to generalise well, the dramatically better computational performance (e.g. predictions for millions of molecules in seconds) and high accuracy have led to increased interest in developing novel, accurate, and efficient methods. Prediction of quantum properties can be performed using general purpose neural networks such as multi-layer perceptrons or graph neural networks. However, state-of-the-art algorithms exploit properties specific to molecules such as 3D atomic coordinates or bond angles.

The design of 3D-aware models has continued to evolve, most often by increasing the expressivity of the feature extraction components of the neural network models. For example, one of the earliest and most well-known architectures, SchNet, introduced continuous-filter convolutions to learn directly from 3D coordinates and atomic types. More recently, DimeNet proposed a message passing scheme that uses directional information given by the angle between atom pairs. Solutions that replace invariant operations (such as in DimeNet) with more expressive equivariant alternatives have also been proposed, for example in PaiNN.

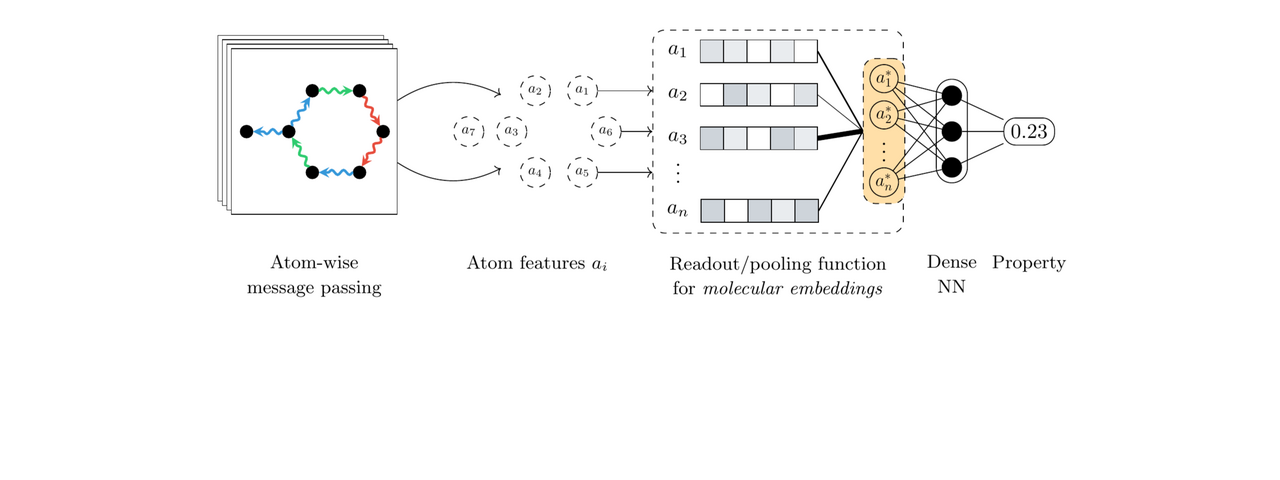
Neural networks designed for molecules naturally operate at the level of atoms, by starting with initial features such as the atom type and coordinates and then iteratively learning more informative representations through convolutions or message passing steps. However, most quantum properties of interest are formulated at the molecular level. As such, a technique for aggregating the learnt atom-level features into a single, molecular-level representation is required. In geometric deep learning and graph neural networks in particular, this responsibility is handled by the readout or pooling function. From a geometric deep learning perspective, the pooling function must satisfy permutation invariance with respect to the atom ordering, meaning that the function must output the same result regardless of the order in which the atom representations are presented. Due to this limiting constraint, most architectures rely on simple pooling functions that satisfy this demand, the standard choices being the sum, mean, or maximum functions.

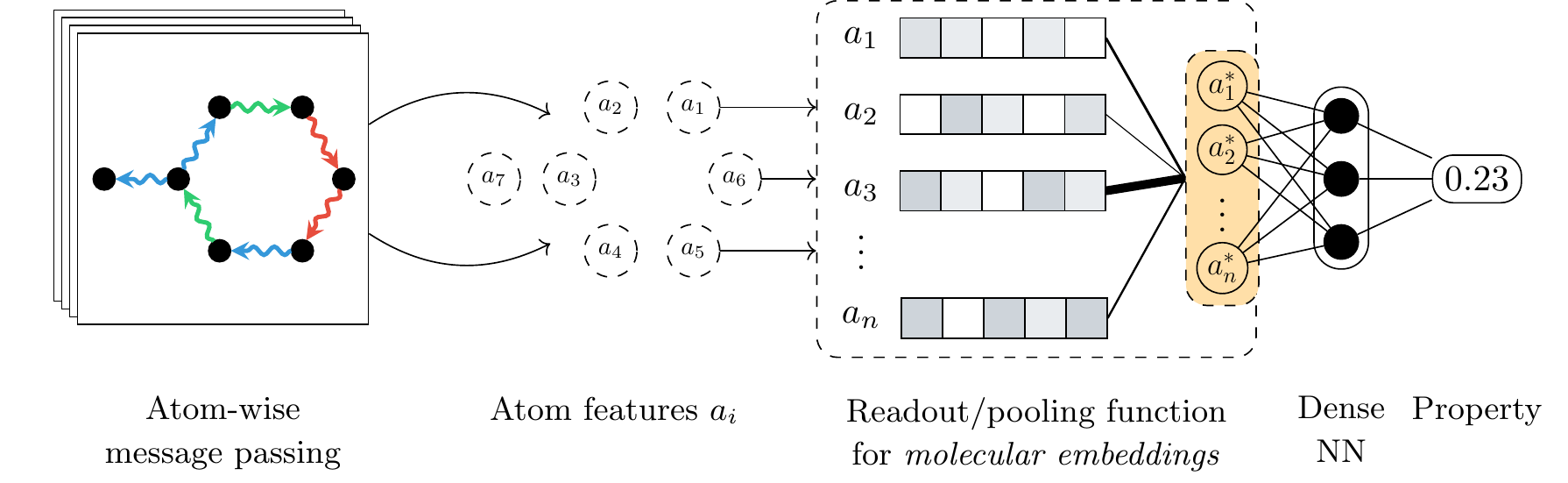
Although the architectures designed for quantum property prediction have continued to advance, most of the efforts have been focused on the atom-level feature extraction components, with the pooling function lagging behind. In our work, we propose an alternative to standard pooling protocols and design a pooling function based on neural networks, more specifically leveraging the attention mechanism that also underlies the famous Transformer architecture. This alternative function is applicable to any quantum property, and to molecular property prediction in general. Furthermore, the attention alternative is a drop-in replacement requiring no changes to any of the other architectural components, regardless of the underlying network.

Here, we used SchNet and DimeNet (more specifically, the updated DimeNet++ variant) as the main architectures and benchmarked the predictive performance of attention-based pooling against the standard choices of sum and mean pooling. Our main focus was on frontier orbital energies such as the HOMO and LUMO since they can be highly localised, or in other words the electron density can be concentrated on a small set of individual atoms or bonds. Such properties are, in theory, not well approximated by neural networks that rely on pooling functions that attribute equal importance to all atom representations, such as sum or mean. In contrast, other types of properties such as the total energy are a function of all atoms and standard functions are a sensible choice. Technically, the proposed attention-based pooling function computes so-called attention scores for each possible atom pair within a molecule, allowing arbitrary contributions from any atom. Moreover, multiple attention layers can be stacked, enabling the modelling of higher-order interactions. Thus, the final molecular embedding can represent both delocalised and localised properties.

Our extensive evaluation includes dataset such as QM7b, QM8, QM9, QMugs, MD17, and OE62, each having its own set of properties and constraints such as dataset size and molecular diversity. Across all kinds of tasks, we were able to consistently improve upon standard pooling mechanisms thanks to our attention-based alternative, for both SchNet and DimeNet++. Remarkably, attention performed better not only for frontier orbital energies, but a wide variety of quantum properties, including extensive and non-local properties like the total energy available in QMugs. Attention-based pooling was also preferable to standard pooling options for tasks operating in a low-data regime, in this case MD17 (between 1,500 and 2,000 molecules), contradicting the view that attention is only helpful on large datasets. For HOMO and LUMO, we have also considered the OE62 dataset and the recently proposed Orbital Weighted Average (OWA) pooling method for more accurate orbital energy prediction. Despite OWA requiring the pre-computation of orbital coefficients and using a second neural network to predict the weight of each atom for the pooling function, we find that attention-based pooling outperforms OWA in all evaluated instances.

Due to the overall success of attention-based pooling on a wide selection of quantum tasks, we believe that it is a general technique that can be adopted by researchers for upcoming architectures. Although classical attention scales quadratically with the number of atoms (both time and space), the pooling function presented here relies largely on self-attention, which benefits from recent innovations that deliver fast and exact attention. More specifically, implementations where the memory utilisation scales with the square root of the number of atoms (so-called “memory efficient attention”), or linearly in time and space (Flash Attention) are available and we have demonstrated their advantages in the paper.