Combinatorial optimization problems are ubiquitous in modern society. It is important to solve these problems efficiently. However, many of these problems are classified as the non-deterministic polynomial-time (NP)-hard or NP-complete complexity classes; these are difficult to be solved on Von-Neumann computers since the number of possible combinations increases exponentially with the number of variables. To solve such problems efficiently, new computational paradigms are needed. Researchers are trying to solve such problems using non-Von computers. Since many combinatorial optimization problems are mathematically equivalent to the Ising model, the Ising machine, a non-Von computer designed to solve the Ising model, is expected to solve such problems efficiently.

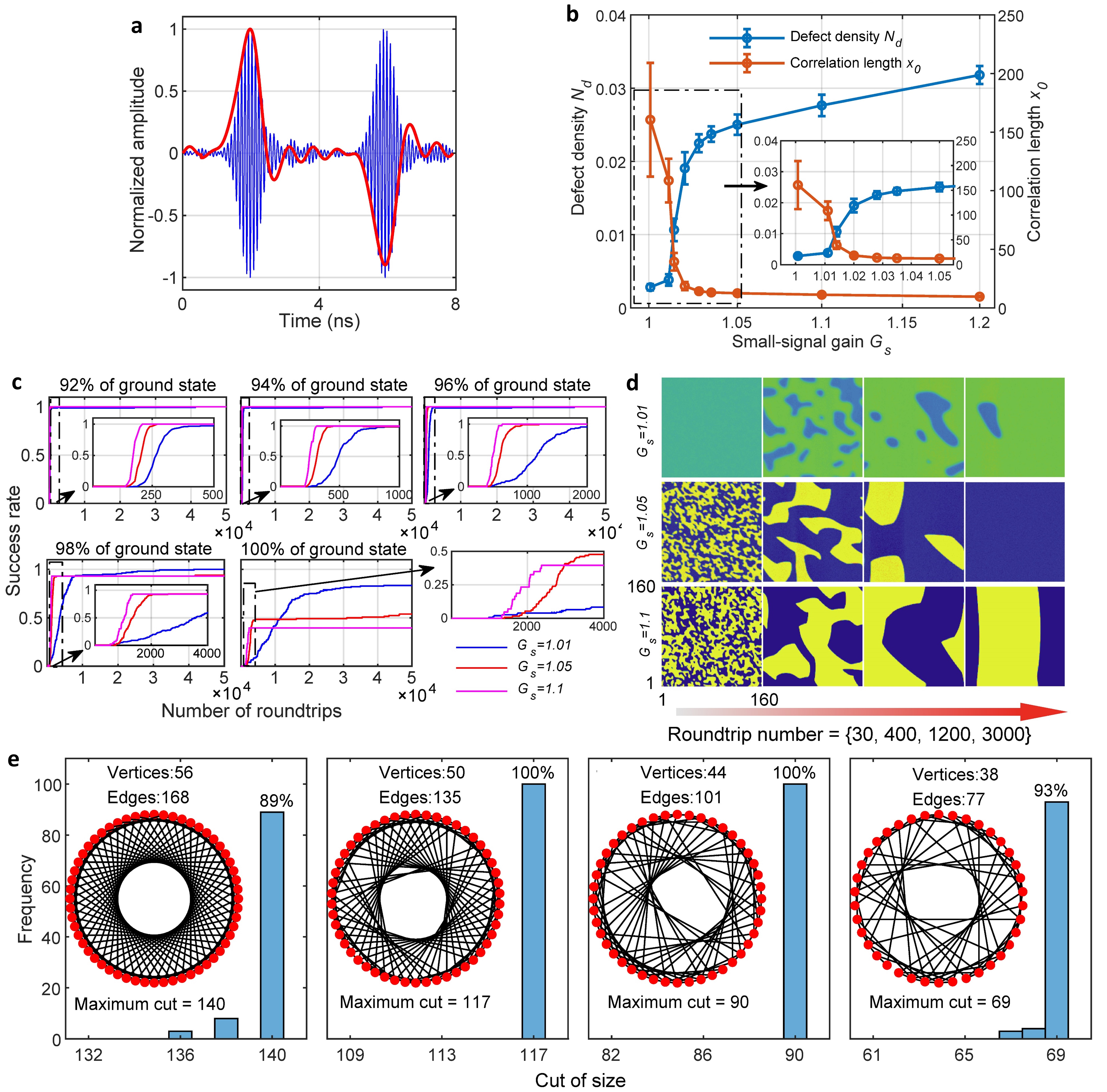
In the article, we proposed a large-scale, stable Ising machine based on an optoelectronic oscillator. In the proposed Ising machine, the artificial Ising spins are represented by the phases of the short microwave pulses generated in an optoelectronic cavity. The number of generated spins was as large as 25,600, and the machine stably operated for over 12 hours. One-dimensional and two-dimensional Ising model simulations were conducted on the proposed Ising machine, and the experimental results suggested the machine has promising potential in finding the low-energy state. In addition, they used the machine to solve max-cut problems, which are well-known NP-hard problems. The results showed that the machine had a high success rate of maximum cut for different graph structures.

The optoelectronic oscillator was used to generate continuous pure microwave signals with uncertain initial phases. In the proposed machine, the oscillations in the optoelectronic cavity are discrete pulses with half the frequency of a local oscillation and locked with a relative 0 or π phase. The binary-phase oscillation can then be used to simulate an artificial Ising spin, e.g., the 0-phase/π-phase state represents up/down spin.

The idea of solving combinatorial optimization problems in the proposed Ising machine is similar to that in the conventional oscillator, i.e., the principle of minimum power dissipation. A specific interaction, defined by the interaction matrix in the Ising model, would change the global loss of the oscillation network and result in the corresponding phase configuration. Phase configuration with minimum loss has the maximum possibility to be selected and oscillate stably. The OEPO network can operate around the minimum-loss state and outputs the corresponding microwave signal whose phase configuration corresponds to the optimal solution of the given Ising problem.