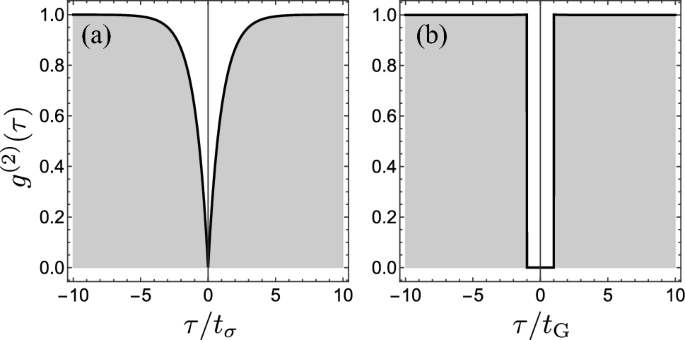
Wulfrunian students had learned in class how Physicists quantify the amount and type of correlations one can find in light, which is with Glauber's so-called g⁽²⁾(τ), a density of two-photon events that take the shapes of Panels a, b and c in Fig. 1 for the textbook cases of uncorrelated (so-called coherent), thermal, and quantum, or single-photon (so-called antibunched) light.

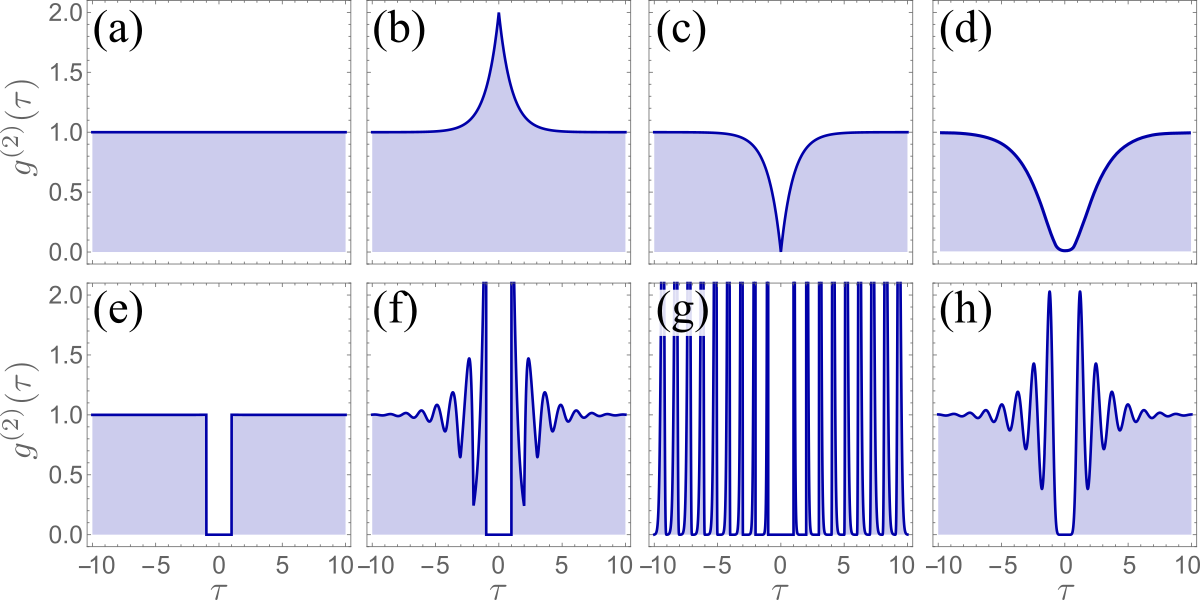
At about the same time, when not in class, we were studying with Juan Camilo López Carreño, Eduardo Zubizarreta Casalengua and Elena del Valle, the properties of something slightly beyond the undergrad curriculum, but not too much, namely, coherently-driven two-level systems. Our interest then was how these did provide either antibunching (two-photon suppression) or subnatural-linewidth spectra (from the Rayleigh-scattered laser), but not simultaneously, as had been implied earlier in the literature [1]. This is indeed possible but a trick is needed to have both attributes together [2]. Interestingly, this trick also came with something unexpected: the shape of the function g⁽²⁾(τ) around τ=0 was modified in a qualitative way. It was becoming flat, as shown in Fig. 1d, in contrast to the steep antibunching one usually deals with (cf. 1c). This gave us a clue that something potentially noteworthy was happening there and that one should look not only at g⁽²⁾(0)—which is what everybody does—to characterize the quality of a single-photon source, but also the slope in its neighborhood.  A completely flat function would indeed provide a g⁽²⁾(0)=0 resilient to time uncertainty, as it would remain g(2)(τ)=0 even if τ is not exactly zero. Since time uncertainty is fundamental to detection [3], we argued that such a flattening was opening a gap able to realize a genuinely perfect single-photon source [2] (in the literature, people refer instead to cases as close to Fig. 1c as possible when they use the adjective "perfect").

Back in the classroom, students needed less trivial photon streams than uncorrelated ones, that are easily generated (sample uniformly N random numbers, order them, done). For thermal and single-photon light, we relied on Camilo's Quantum Monte Carlo simulations of such processes, which are available as supplementary material of earlier papers [4] or upon direct queries. To avoid relying on external data or emails, inspired by the results described above, I proposed students to simply enforce in their Poisson stream the condition that photons can never get closer than a given time gap t_G. This is easy and a good programming exercise. One can simply remove the extra photons, as shown in Fig. 2 (one can also displace them rigidly by inserting a time gap as a spacer for all subsequent photons):

My most diligent students came back with photon correlations for their hand-made single-photon sources that I did not like at first. It is shown in Fig. 1(f), while I was expecting Fig. 1(e). The arrogance of the half-witted teacher made me think that their code was incorrect and that they had either produced incorrect streams or that their computation of the correlation function was flawed. I did not like that my alleged perfect single-photon source would feature oscillations. I do not remember which technique was implemented by the first group (histogram of time differences or explicit intensity correlations by products of rotating arrays), but I remember which group this was: Ceri Neale and Luke Collins. When another group, Dylan Weston and Joel Warner, reported independently the same result, it was time to think. I stopped explaining them that such positive correlations were not possible because as a density of two-photon events, g⁽²⁾(τ) is indifferent to the presence or not of intermediate photons which could furthermore be lost or not detected without affecting the correlations for a given time delay, so what we were removing locally could not propagate oscillations. With the clue that it might be correct, I got a feeling that this was a manifestation of the Monty Hall paradox, whereby seemingly irrelevant information turns out to reshuffle probabilities [5].

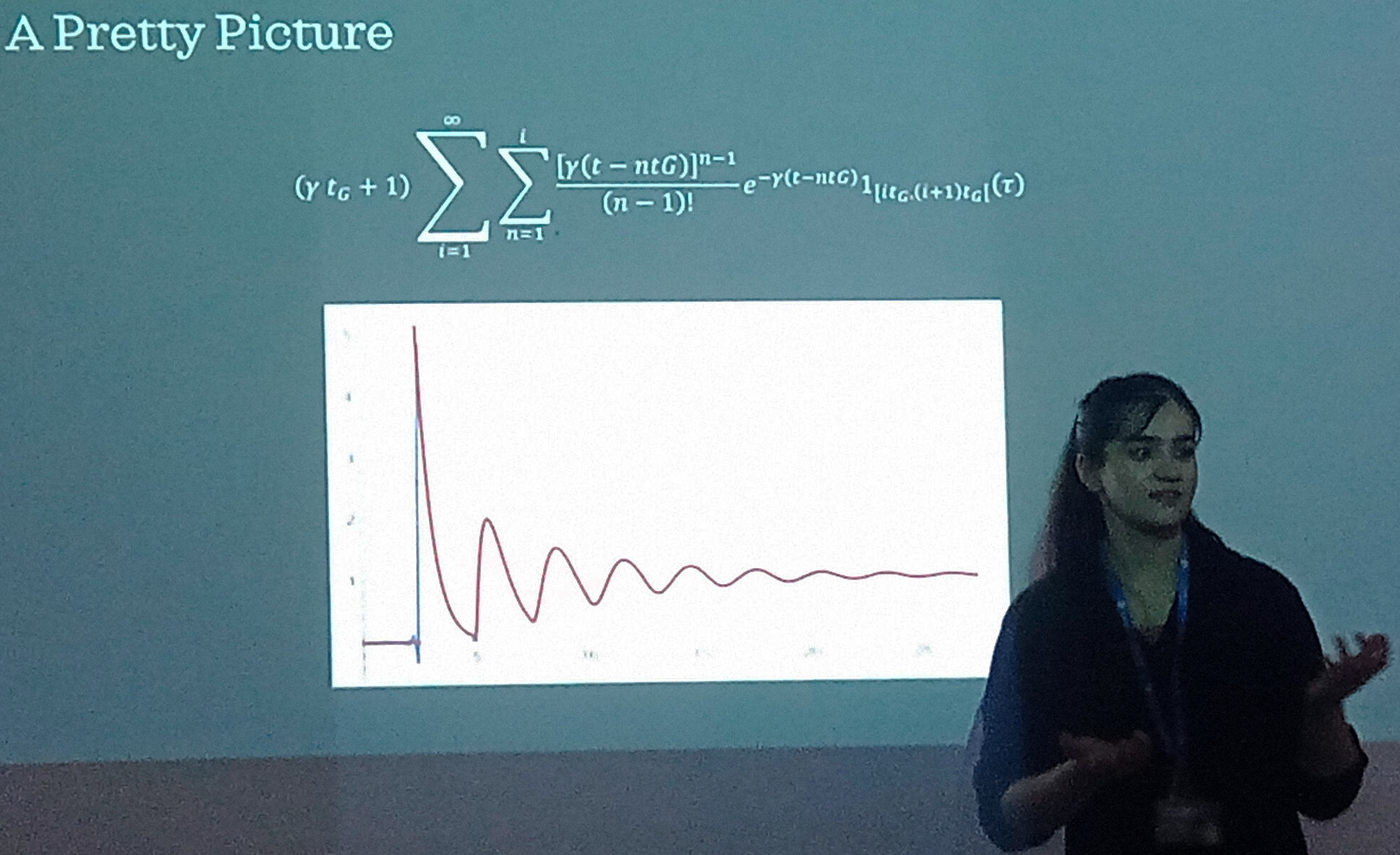
I would have loved to keep this problem within the class but students go by the rhythm of their academic calendar and by the time we made a bit of progress, they had graduated already.  I thus asked a professional researcher, Sana Khalid, a PhD student, to work out the probabilities to reconstruct the function. Its first chunk for 0<τ<2t_G was fairly immediate to obtain, and could be understood from the photon opening a gap as an heralder for the next one [6]. Sana's mathematical dexterity, following preliminary attempts from another skilled undergrad (Damien Pitts), then found the most elegant way to generalize the result to all photons, in terms of the waiting-time distribution w(τ) which, unlike g⁽²⁾(τ), is quite intuitive. We could then complete the description following steps from Reynaud and Kim et al. (those being not Wulfrunian students but big names of the field [7]) to link g⁽²⁾ and w. The picture below is Sana first presenting her formula, plotted in red on top of a brute-force calculation of the Laplace transform of a series' summation of the waiting times:

Once we got the analytical result, and with it the full understanding of what was going on, we  were also able to bring the correlation function in a regime not easily accessible numerically: that of removing a lot of signal by opening a huge time gap. There we found the correlation function took the shape shown in Fig. 1g, which by then was not a surprise in itself as Sana's formula is precisely an iteration of each photon heralding its successor.  The surprise was the sudden realization that this stationary source was turning into its exact opposite: pulsed emission. A perfect continuous wave single-photon source acquires the character of a pulsed one, where the photon-ordering is imprinted from outside. Our source, however, gets its correlation from inside. The oscillations in g⁽²⁾(τ), familiar in other contexts such as Rabi oscillations, are thus not detrimental to single-photon emission, but are instead a consequence of it, if it becomes good enough. We also understood how other, familiar types of single-photon emission could similarly be produced in the same way, not by opening a rigid gap but by pushing photons according to a given distribution. No need of Quantum Monte Carlo anymore, just standard one. The paradigmatic single-photon source thus arises from a Poisson repulsion on top of the Poisson stream itself. This explains, among other things, why such sources, however small is their g⁽²⁾(0), can never be "perfect": in photon clicks like in life, one will always get unlucky twice and get two Poisson bursts to produce coincidences. A time gap in the form of a non-Poissonian repulsion is needed for perfect single-photon emission.

The latest development behind this paper comes from an email of a frequent co-author, Elena del Valle, who after reading our arXiv preprint, sent us a series of corrections and comments of which I reproduce number 2:

2. The system is related to the problem of an ideal gas (no long-range interactions) of hard spheres (diameter = time gap) in 1D and looking at its pair distribution (second order correlations in space) and structure factor: https://en.wikipedia.org/wiki/Radial_distribution_function

That came as a little disappointment because this is precisely the sort of thing I should have known myself, also because our analytical formula had been (not surprisingly, with hindsight) derived already, namely, on Christmas day of 1926 in this hard-sphere context. This was by Jan Albert Prins, who had connected diffracted intensities to molecular arrangements but does not seem to have been much remembered for that [8]. His method and all others we found in its wake were quite different than ours, which is much simpler as rooted in waiting times (something natural when you literally wait for the next photon, not so much for atoms already in place in a crystal). But this suggested that we had unraveled a connection between condensed-matter phases and various types of quantum light. Interestingly, although the pair correlation function is typically denoted g², Glauber himself seems to make no mention of it anywhere. We are currently investigating such connections with the vision that there is a thermodynamic-looking description of quantum light where space gets traded for time and where perfect single-photon emission is not to be found in g⁽²⁾(0) but in the full "structure factor" where the flatness of g⁽²⁾(τ) indeed, as well as the oscillations that demark "crystallization" (in time) of light, are the attributes to look at. With the understanding that some sort of photon repulsion is needed to flatten the "pair correlation", we got the intuition that a cascade from a multilevel structure would achieve that, as each photon would need to undergo a chain of random samplings, each contributing a Poisson push, endowing the photons with a less random, more correlated, more viscous grip on the time it takes to finally be emitted. I was mildly aware that experimentalists worry about "shelving" or "intersystem crossing" and how an in-betweener makes their g⁽²⁾(τ) acquire elbows. Were they having their perfect single-photon emitters all along? Not quite, in their scenario, there is no flattening at small times (no gap opening), just the elbow. A real cascade, however, brings you there: we were quite pleased to see a variation of the characteristic shape of the perfect single-photon source emerge in a model that makes the photon go through such a cascade (compare Figs. 1h & f). Something not done "by hand" to keep students busy, but the result of a master equation, if you insist on it, although the key of the argument remains a statistical one rooted in time ordering from compound random events. What started as a warming-up exercise for the classroom could well turn out to call for photonic experts to reconsider how they understand, characterize, and even design, single-photon emission.

References: 

1. H. S. Nguyen et al. Ultra-coherent single photon source. Appl. Phys. Lett., 99:261904, 2011; Matthiesen et al. Subnatural linewidth single photons from a quantum dot. Phys. Rev. Lett., 108:093602, 2012.
2.  J. C. López Carreño et al. Joint subnatural-linewidth and single-photon emission from resonance fluorescence. Quantum Sci. Technol., 3:045001, 2018.
3.  E. del Valle et al. Theory of frequency-filtered and time-resolved n-photon correlations. Phys. Rev. Lett., 109:183601, 2012.
4. J. C. López Carreño et al. Frequency-resolved Monte Carlo. Sci. Rep., 8:6975, 2018. 
5. F.P. Laussy. The Monty Hall problem in Quantum Optics.
6. E. Zubizarreta Casalengua et al. Two-photon correlations in detuned resonance fluorescence. Phys. Scr., 98:055104, 2023.
7.  Reynaud, S. La fluorescence de résonance: étude par la méthode de l’atome habillé. Ann. Phys. 8:315, 1983; Kim et al. Correlations between successively emitted photons in resonance fluorescence. Opt. Commun. 62:385, 1987.
8. F.P. Laussy. The pair correlation function. laussy.org's Blog:Science.
9. E. Zubizarreta Casalengua et al. Photon liquefaction in time. arXiv:2312.17732, 2023.
10. F.P. Laussy. A mechanism for a perfect single-photon source. laussy.org's Blog:Science.