The standard model of particle physics, the most successful description of our universe is formulated in terms of gauge theories. Elementary particles and the excitations of the gauge fields that mediate interactions between them make up the standard model. While gauge theories are fundamental in particle physics and require high energy probes (like a collider) to study them, they may emerge naturally in certain condensed matter systems. In these systems, emergent gauge fields describe the low energy physics and can be more easily studied in a laboratory. Quite often, they are intimately linked to the quantum  entanglement and topological properties of the many-particle system at hand. These connections are routinely manifested by excitations that are fractional. They are not bound to each other  but can only be created or destroyed locally in pairs and carry fractions of an electronic quantum number.

A quintessential example is a quantum spin liquid (QSL). While the elementary excitations of a magnetically ordered system (e.g. anti-ferromagnet) are magnons with spin quantum number 1, the quasiparticles of a QSL may carry only a fraction of this quantum number. A celebrated model for a QSL is the Kitaev honeycomb model, a two-dimensional (2D) honeycomb lattice of interacting spins. In this model, a local spin flip fractionalizes into a pair of emergent gauge field excitations - visons , and Majorana fermions which represent half of an ordinary fermion. Surprisingly, there is a large class of materials believed to be described by the Kitaev model with additional perturbations— known as Kitaev materials. Understanding how these perturbations influence the nature and signatures of the fractional quasiparticles is crucial for detecting and controlling them in real materials. One major effect of these perturbations is that they make the visons dynamical degrees of freedom. Despite some experimental evidence suggesting the presence of a spin liquid in certain Kitaev materials, strong sample dependence has hindered the unambiguous detection of an emergent dynamical gauge field.

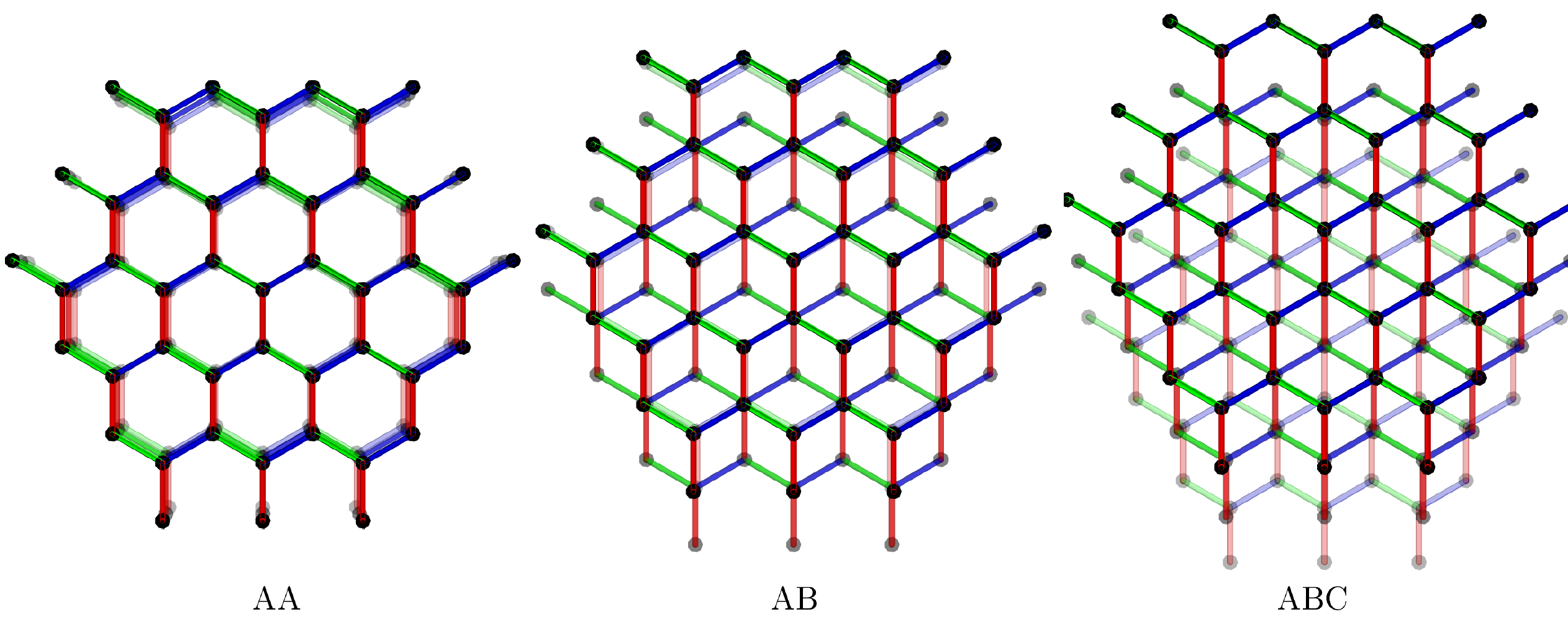
An often-overlooked aspect of candidate materials is their three-dimensional (3D) structure composed of weakly interacting 2D layers. It is important to understand how the quasiparticles of the purely 2D model behave when a third spatial dimension (stacking axis) is introduced. Our work addresses this question in detail by analyzing the dynamics of the emergent gauge field in simplified models of layer-stacked Kitaev spin liquids.

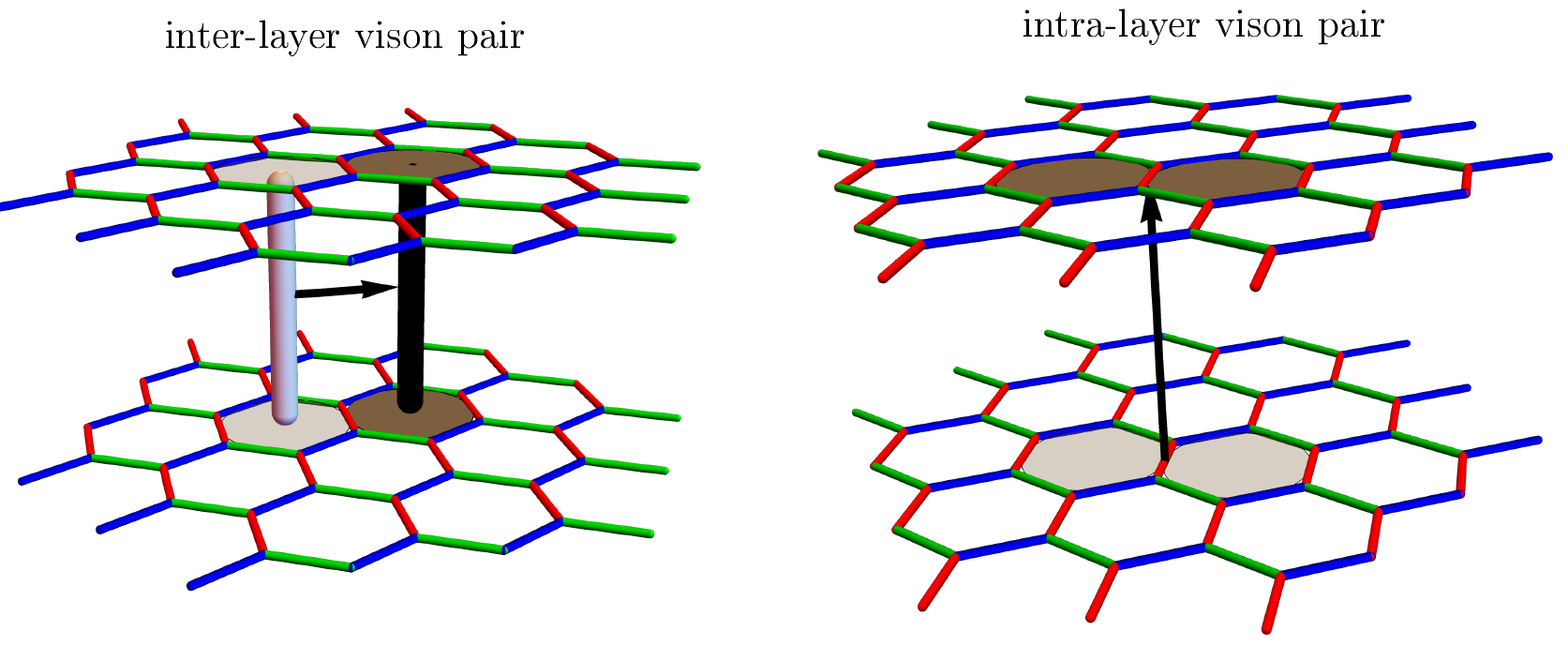
Topology prevents a single vison from being created or annihilated locally within a layer, thus blocking the motion of individual visons between layers. Conservation laws further restrict their in-plane motion, rendering single visons completely immobile. When the layers are AA stacked, the parity of visons (odd or even number) in a given hexagonal column is conserved. For AB and ABC stacking, however, conservation laws take the form of 2D "sheets" that criss-cross the system. Single visons cannot cross a sheet, thus are effectively  trapped by the sheets. Using these principles, we show that visons form pairs - interlayer and intralayer pairs, which become mobile due to the weak interlayer coupling. While an interlayer pair is constrained to move parallel to the layers, an intralayer pair can only move between layers. Remarkably, the sheet conservation laws put further constraints on their motion. While in an AA stacked model, interlayer pairs have a fully 2D motion, they are constrained by the sheets to move along 1D channels in AB and ABC models. We further calculate the dispersion relations of these excitations and describe how spatial anisotropy in spin-spin interactions as well as magnetic fields profoundly affect their propagation.

This unusual mix of excitations with different mobility constraints in a rather simple model may be used as a starting point to predict novel signatures of fractional quasiparticles in Kitaev materials. For example, one could use a laser pulse to create a high density of excitations at the top surface of a sample and track using optical measurements how they diffuse in space as determined by their dimensionality. Thus, this approach transforms the layered nature of spin liquid materials from a perceived drawback into a valuable tool for exploring fractionalization in real materials.