Quantum Chemical Accuracy from Density Functional Approximations via Machine Learning
Published in Electrical & Electronic Engineering

Modern machine-learning (ML) techniques have proved to be a powerful approach in the molecular sciences for predicting the properties of a system without having to solve the electronic Schrödinger equation explicitly. By introducing an ML model, it becomes possible to bypass computationally expensive quantum chemical calculations that yield approximate solutions of the Schrödinger equation, obtaining results at the same level of accuracy via comparably inexpensive inference. Importantly, once trained, the computational cost of an ML prediction remains the same regardless of the expense of the original reference calculations used to train the model. This includes reference calculations performed at the level of widely used density functional theory as well as very costly coupled-cluster (CC) calculations, which remain the 'gold standard' of accuracy among standard electronic structure methods. Given that the computational overhead of explicit CC calculations scale as the seventh power of the number of atoms in the system, the advantage of using an ML model to predict the outcomes of CC calculations becomes clear. However, since a CC calculation for a single molecular geometry can take many hours or even days, the amount of training data that can be generated within a reasonable time frame is very limited. Hence, the ML models used need to be highly data efficient in order for them to be capable of producing accurate results with a minimal number of training samples.
In previous work, we drew inspiration from the Hohenberg-Kohn theorem of density functional theory (DFT), which prescribes a one-to-one mapping between the external potential of a system of electrons and the ground-state density of the system, and we constructed an ML model of this map, which we call the ML-Hohenberg-Kohn (ML-HK) map, that could successfully predict electron densities from input potentials for a range of small molecules. The fact that any property of the system is determined by the electron density suggests that this function is an ideal descriptor of these properties. Consequently, we were able to construct a second ML model that could predict a property such as the total energy of the system using the predicted density as an input.
DFT establishes the existence of an exact density functional capable of delivering the exact ground-state energy. Although this exact functional is unknown, it seemed natural to consider trying to learn highly accurate CC energies from the ML-HK map. However, DFT specifies that the correct energy should be obtained as a functional of the self-consistent density, which meant that we would need to use electron densities generated from CC calculations. Unfortunately, these are not readily available in most quantum chemistry packages, as a CC density is not a required part of a CC calculation. We ultimately realized that the flexibility of ML would allow us to overcome this limitation, allowing us to short-circuit the need for self-consistency and, thereby, bridge the gap between the DFT and CC worlds.
Specifically, we constructed an ML model to predict the CC energy as a functional of the DFT density. While this may seem counter-intuitive at first, one simply needs to remember that ML is not bound by the rules of self-consistency but will learn what it is trained to provided only that is has sufficient training data to to so.
In our most recent work, therefore, we show that it is indeed just as easy to train our ML model to predict CC energies from the DFT densities as it is to train it to predict the DFT energies from the self-consistent DFT densities with no significant loss in accuracy! Encouraged by these results, we decided to embark on another exploration of whether the difference between the DFT and CC energies could be learned as a functional of DFT densities as well. This approach (called Δ-DFT) allowed the ML model to be trained with far fewer reference CC calculations, leading to prediction of CC energies at the cost of a DFT calculation.
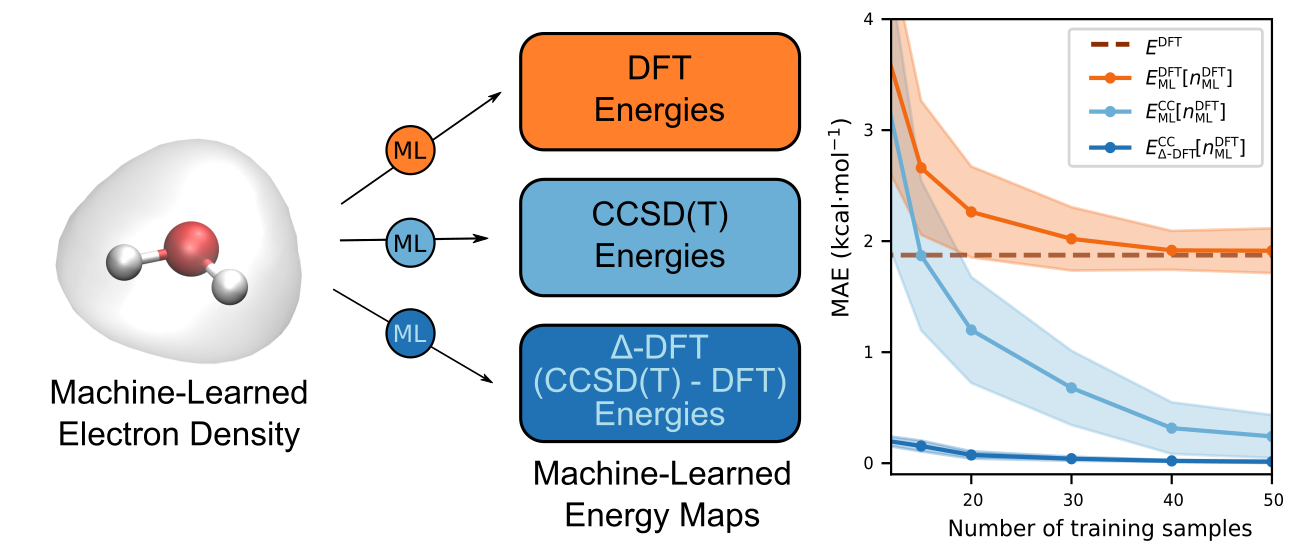
With this Δ-DFT model in hand, we demonstrated a number of its important features. First, we showed that the model could be used to generated first-principles molecular dynamics trajectories of molecules at CC accuracy but at the cost of generating them via DFT. In addition, using multiple time-stepping methods, we showed that this cost could be reduced even further. Second, we showed that using the electron density as a descriptor allowed us to combine multiple similar but non-identical molecules into a joint model capable of simultaneously predicting the CC energies of the different molecules with a higher accuracy than models trained on each molecule individually. We view this a major step towards creating a model that is transferable across a wide range of molecules.
If you are interested in finding out more about our work, you are welcome to have a look at our paper published in Nature Communications 11, 5223 (2020), https://doi.org/10.1038/s41467-020-19093-1 or via the following link: https://rdcu.be/b8BOG
Follow the Topic
-
Nature Communications

An open access, multidisciplinary journal dedicated to publishing high-quality research in all areas of the biological, health, physical, chemical and Earth sciences.
Related Collections
With Collections, you can get published faster and increase your visibility.
Women's Health
Publishing Model: Hybrid
Deadline: Ongoing
Advances in neurodegenerative diseases
Publishing Model: Hybrid
Deadline: Mar 24, 2026



Please sign in or register for FREE
If you are a registered user on Research Communities by Springer Nature, please sign in