Can quantum algorithms accelerate the mixing of nonreversible Markov processes? This is the central question addressed in our study.   While most quantum speedups for Markov chain sampling have been established in the reversible setting, many natural processes are inherently nonreversible, and efficient quantum algorithms for such cases remain less understood.

Markov chains are widely used to model stochastic dynamics in areas such as physics, biology, and machine learning. A Markov process is a sequence of random variables defined on a given state space, where the next variable is drawn according to a probability distribution that depends only on the current state. This lack of memory, the Markov property, greatly simplifies both analysis and simulation, as the full trajectory need not be retained to predict the future. Ergodic Markov processes are such that the distribution of the n-th variable converges to a stationary distribution independent of the initial state. Their mixing time quantifies the timescale of this convergence and will play a central role throughout this chapter. A sufficient condition for a chain to admit a specific probability measure as stationary distribution is to be reversible with respect to this distribution. While most quantum speedups for Markov chain sampling have been established in the reversible setting, many natural processes are inherently nonreversible, and efficient quantum algorithms for such cases remain less understood

Our work investigates two quantum methods for accelerating the mixing of nonreversible Markov chains.

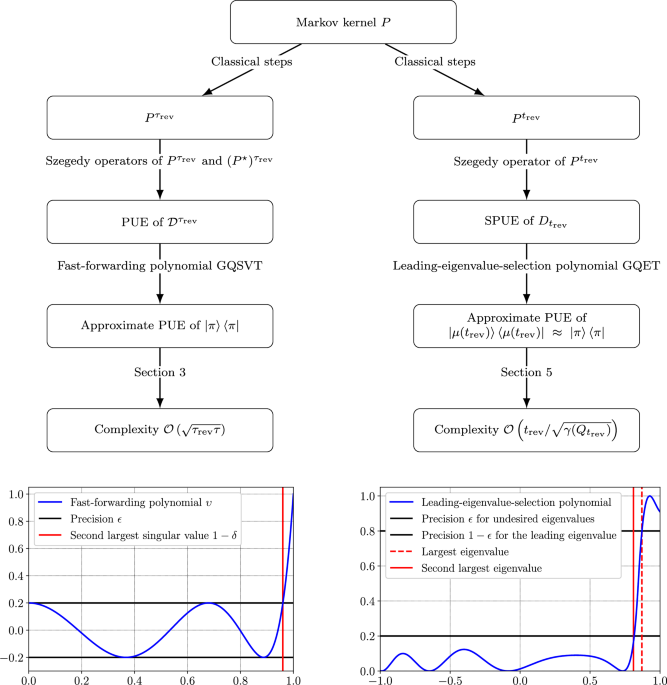
We first analyze a method based on a generalized quantum singular value transform (GQSVT) of the curved discriminant. This approach generalizes techniques from the reversible setting and provides a quadratic speedup under appropriate conditions. However, it requires the simulation of the time-reversal of the Markov chain, a significant practical limitation when dealing with nonreversible dynamics.

To address this, we develop a second method, based on a generalized quantum eigenvalue transform (GQET) of the flat discriminant. This alternative does not require knowledge or simulation of the time-reversal. Instead, it relies on a new concept we introduce, termed reversibility on π-average, which captures a property weaker than reversibility but sufficient to ensure quantum speedup.

Our results demonstrate that quantum algorithms can offer meaningful acceleration even in the absence of detailed balance, thus extending the frontier of quantum advantage in sampling and stochastic simulation. Such an up-to-exponential quantum speedup goes beyond the predicted quadratic quantum acceleration for reversible chains and is likely to have a decisive impact on many applications ranging from statistics and machine learning to computational modeling in physics, chemistry, biology and finance.