Time-resolved Coulomb collision of single electrons
Published in Physics
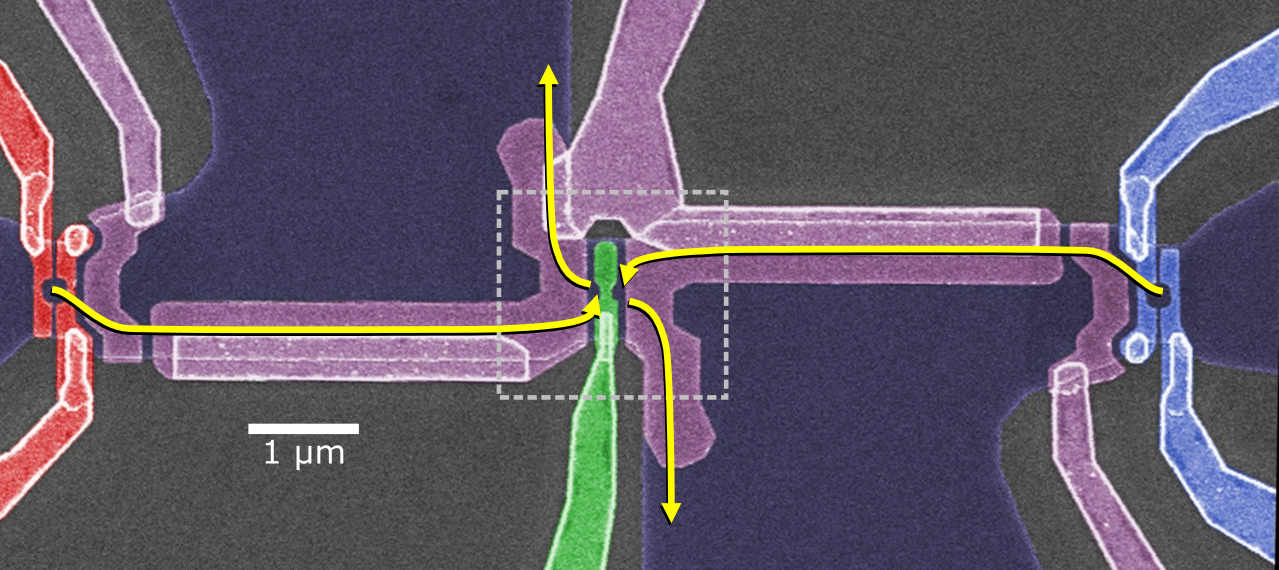
A (very compact) history of tiny fermion colliders
The chiral states at the edge of a two-dimensional conductor in a perpendicular field can behave like waveguides for electrons. These edge states exhibit rich physical phenomena including the quantum Hall effect from which the SI Ohm is routinely derived. Ballistic transport of electrons in these states can often resemble a solid-state analog of quantum optics. Electronic versions of optical systems, like the Hanbury Brown Twiss (HBT) and Mach Zehnder interferometer (MZI) have been implemented, swapping photons for electrons. This approach explores the possibilities of ballistic transport for applications such as sensing or quantum information transfer.
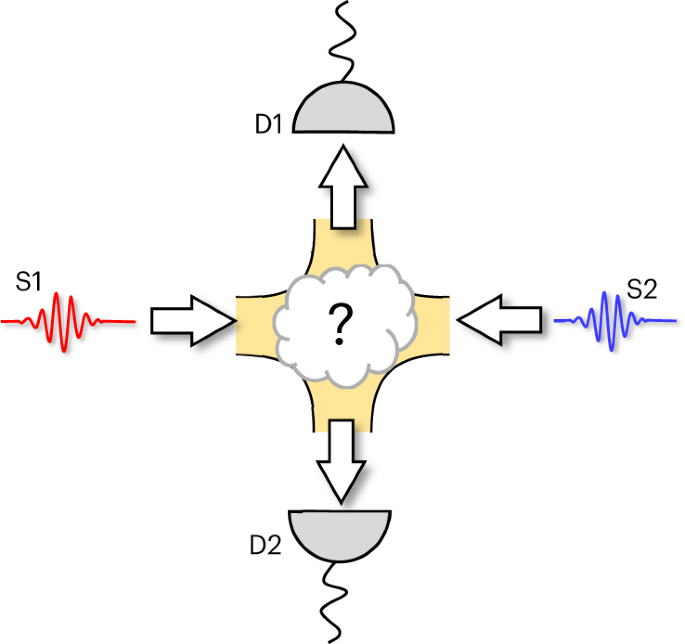
On-demand electron sources enable a kind of particle collider (Figure 1a) somewhat like the optical Hong-Ou-Mandel (HOM) interferometer but with electrons instead of photons. This device can probe (fermionic) quantum exchange statistics and the indistinguishability of the injected particles. This was demonstrated using collision of on-demand electrons injected near the Fermi energy [3]. A suppression of noise was seen when electron arrival at the beam splitter was synchronised. The origin of this effect is a constraint of the Pauli exclusion principle imposes; identical electrons must take separate outputs.
Interestingly, what was not detected in those experiments was any sign of the Coulomb interaction. This suggests electrons near the Fermi energy are strongly screened by the quantum Hall bulk and the Coulomb repulsion is masked. While the HOM geometry has since been used with other sources and to perform wavefunction reconstruction of electrons, the Coulomb interaction does not seem to play a major role in those cases.
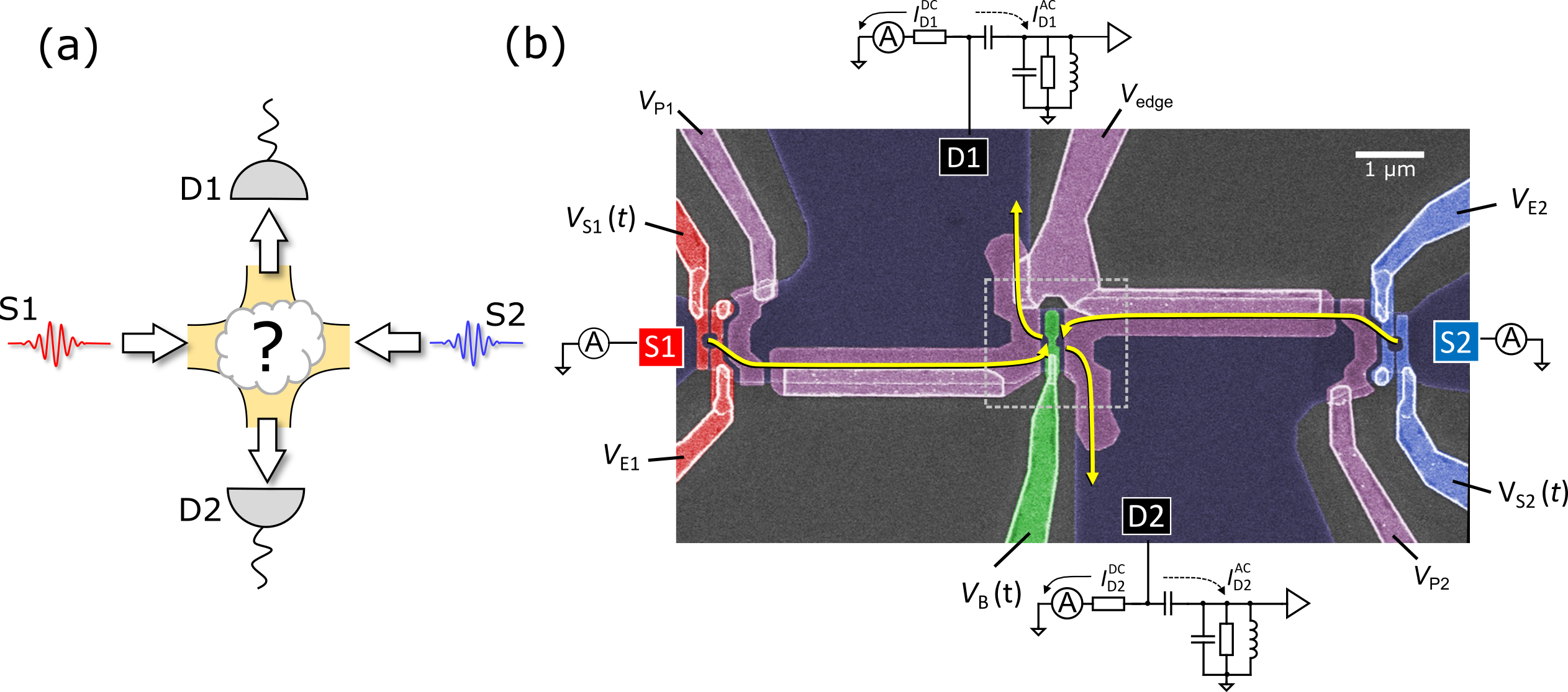
(b) Practical implementation of a collider using electron pumps (red and blue gates) a beam splitter (green gate) and current noise measurements.
Electron collision in a different regime?
At around the same time as the first on-demand electronic HOM experiments were performed [3], an electron source emitting high energy ballistic electrons was demonstrated [4]. These devices were originally developed for high accuracy charge transfer for metrology (i.e. to directly realise the ampere by `counting electrons’) but they also support ballistic transport along quantum Hall edges. We suspected that these devices operate in a different regime, with electrons spatially separated from the quantum Hall bulk and with a weaker screening of the Coulomb interaction. This would constitute an interesting platform where Coulomb effects can be detected and controlled and a step forward for electron optics devices using Coulomb interactions for sensing or two qubit operations.
The electron collider
To explore this possibility, we developed the electron collider shown in Figure 1b. This uses surface gates on a GaAs heterostructure to define pumps that support high energy (>100 meV) emission and well-defined emission timing (<5 ps). We use this device to detect the outcomes of electron collisions between electrons of equal energy, but with varying arrival time Δt = t2 - t1 , which determines whether electrons collide or miss each other. We also vary the height of the barrier EB used as a beam splitter, a component which typically provides information on electron energy [4]. For readout, we measure the mean current distribution and the shot noise fluctuations. Taken together, these enable a very detailed analysis of the detector collision statistics Pnm, the probability of electrons leave in the same (P02 or P20) or different (P11) output channels (P20 + P02 + P11 = 1).
Coulomb Collisions
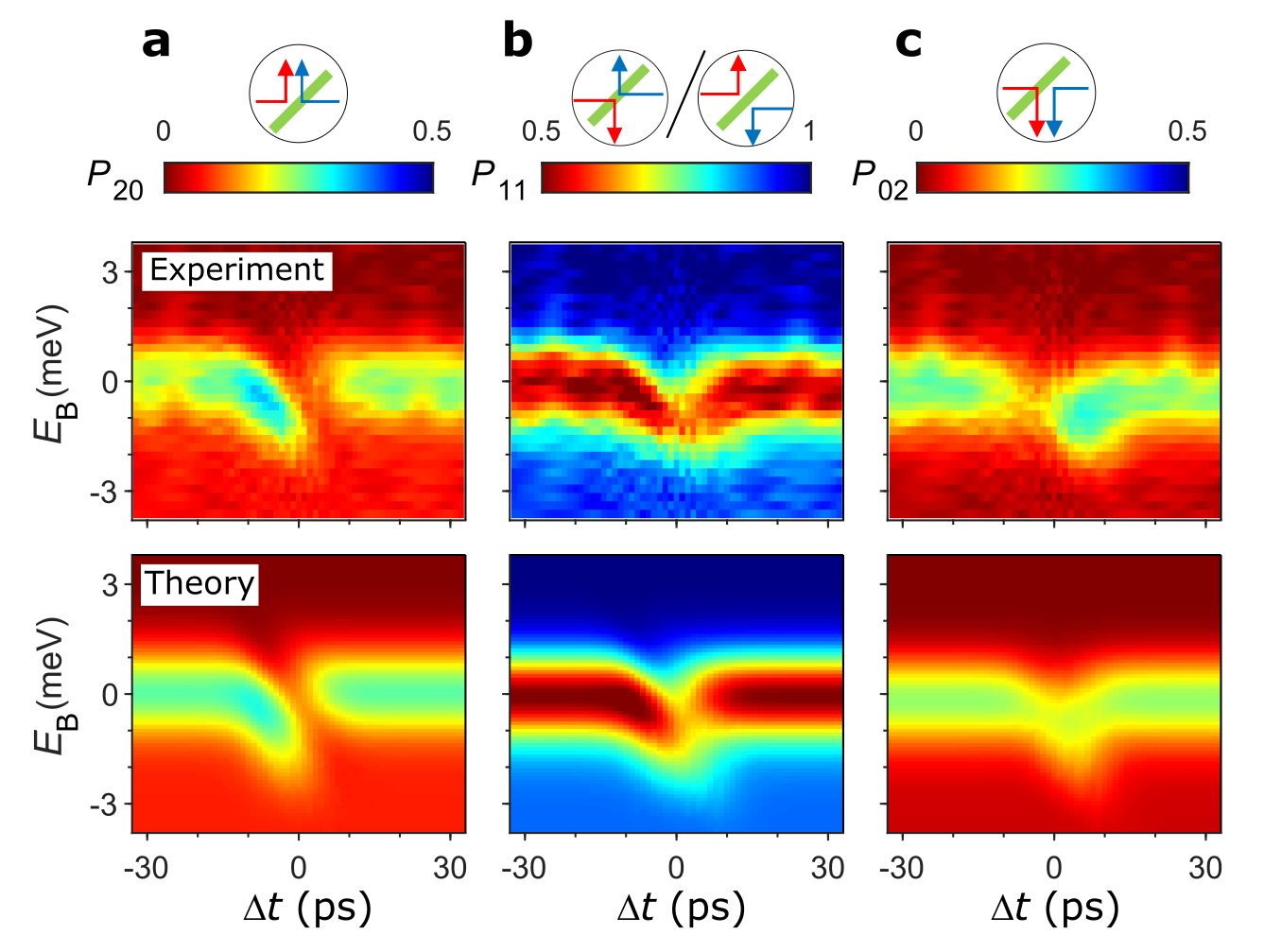
Our paper reports the experimental signatures of interactions between the electrons. Effects observed include: perturbations in the programmed barrier height at which electrons are blocked; imbalances in current distribution; and partition noise suppression. All of these effects can all be seen in the partition statistics in Figure 2. For large |Δt|, where electrons miss each other, each panel shows the feature expected (a peak or dip) when the barrier height crosses the threshold of transmission for the electrons (labelled EB = 0 here). This feature is strongly perturbed when the electrons arrive close enough in time to interact near Δt=0.
Looking at this effect in more detail, we see that in the trivial non-interacting case (e.g. |Δt| > 20 ps) at EB = 0 the statistics reflect a simple mixture of the four possible outcomes, P20 = P02 = 0.25 and P11 = 0.5. Near Δt=0, the barrier height EB at which this thresholds feature appears shift by ≈ 1 meV. There is also asymmetry such that P20≠P02. At some time delays, the minimum value of P11 > 0.5, which corresponds to a reduced noise. The properties of this data lead us to believe that this is an almost unscreened Coulomb collision.
Understanding trajectories
While a finite width in energy-time injection distribution which we detected in our previous work [5] gives a slight blurring of the data, all of these signatures match well with a theoretical model of scattering in a saddle point potential dominated by Coulomb repulsion. The values of the parameters used in the computation, whose results are shown in the lower panels of figure 2, suggest an almost unscreened interaction in this energy range, completely different from collisions at the Fermi energy [3].
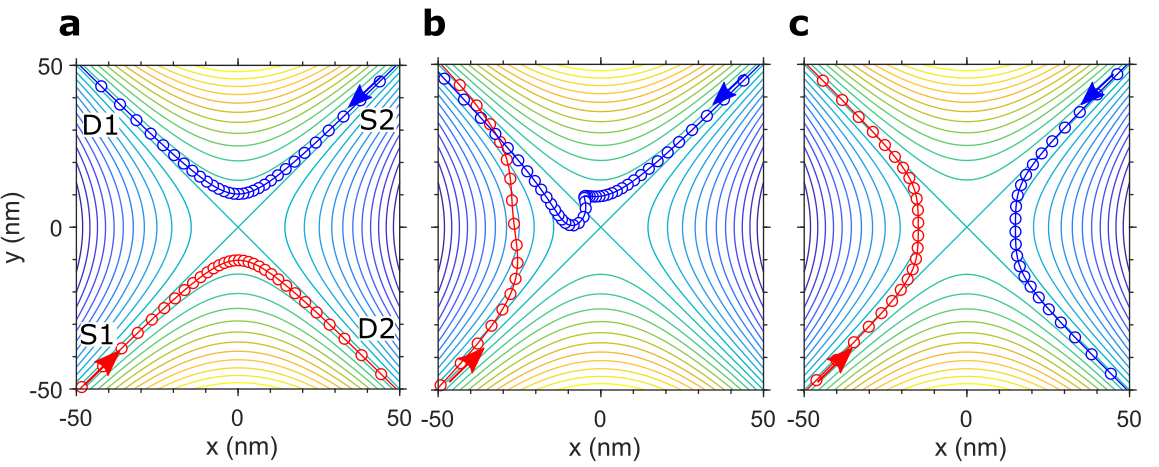
Who goes first?
The Coulomb-dominated model predicts some distinctive effects. One is an order-of-arrival effect which causes the first electron to reach the saddle point and then "hold the ground", repelling the other electron without having its ultimate trajectory changed (see Figure 3b). This gives preferential transmission of one electron depending on the relative arrival time. We have confirmed that this is present in the experimental data, along side the more straightforward outcomes of missing each other (Figure 3a) and synchronized collision (see Figure 3c).
An electron collision 'trilogy'
Also published in Nature Nanotechnology are results from German National Metrology Institute, PTB [6]. They have performed electron collision experiments with a single shot detection scheme and lower electron energy. These are further accompanied by results from the Institut Néel in France whose experiment used electrons 'surfing' in surface acoustic wave (SAW) minima which sweep electrons along two parallel channels [7] until they meet at a barrier.
Each group saw in their data the strong manifestation of the Coulomb interaction as electrons approach each other at a partitioning barrier. In the NPL and PTB cases, electrons are riding high up on the device edge potential. When they meet they 'dance' around the saddle point to avoid each other. In the SAW case, the repulsion tends to pin each electron into its own channel. In each case a theoretical model based on Coulomb interaction alone explains the partition statistics.
This neat collection of results provides clear evidence for the significance of Coulomb interactions when you depart from the heavily screened low energy regime. This is a key step towards controlling electronic interactions at the single electron level which can be used to create interactions between flying qubits [8].
References
[1] Time-resolved Coulomb collision of single electrons, J.D. Fletcher, W. Park et al. Nature Nanotechnology 18, 727 (2023)
[2] The Fermionic Hanbury Brown and Twiss Experiment, Henny et al. Science 284, 296 (1999);
An electronic Mach–Zehnder interferometer, Ji et al. Nature 422, 415 (2003)
[3] Coherence and Indistinguishability of Single Electrons Emitted by Independent Sources, E. Bocquillon et al. Science 339, 1054 (2013). cf. Minimal-excitation states for electron quantum optics using levitons. J. Dubois et al. Nature 502, 659 (2013).
[4] Clock-Controlled Emission of Single-Electron Wave Packets in a Solid-State Circuit, J.D. Fletcher et al. Phys. Rev. Lett. 111, 216807 (2013)
[5]Continuous-variable tomography of solitary electrons J.D. Fletcher et al. Nature Communications 10, 5298 (2019)
[6] Two electrons interacting at a mesoscopic beam splitter N. Ubbelohde et al. Nature Nanotechnology 18, 733 (2023)
[7] Coulomb-mediated antibunching of an electron pair surfing on sound J. Wang et al. Nature Nanotechnology 18, 721 (2023)
[8] Semiconductor-based electron flying qubits: review on recent progress accelerated by numerical modelling, H. Edlbauer et al. EPJ Quantum Technology 9,21 (2022)
Follow the Topic
-
Nature Nanotechnology

An interdisciplinary journal that publishes papers of the highest quality and significance in all areas of nanoscience and nanotechnology.

Please sign in or register for FREE
If you are a registered user on Research Communities by Springer Nature, please sign in