Topological states in non-integer dimension

Fractals are everywhere...
Let's play a game. We start with a triangle, find the middle points in its edges, and connect them with lines. Now remove the smaller triangle that is defined by those points. The figure that we obtain has three smaller triangles. For each of them, we can repeat what we did with the original one. We obtain nine small triangles. Then, twenty-seven and eighty-one. With enough patience, one arrives at an infinite number of infinitesimally small triangles. The figure we constructed in our game is neither one- nor two-dimensional, but something in between: in fact, it has dimension log2(3)~1.58. This structure, called a Sierpinski gasket, is not the only one to present this unusual feature. In fact, there is a whole class of mathematical structures like this that are called fractals.
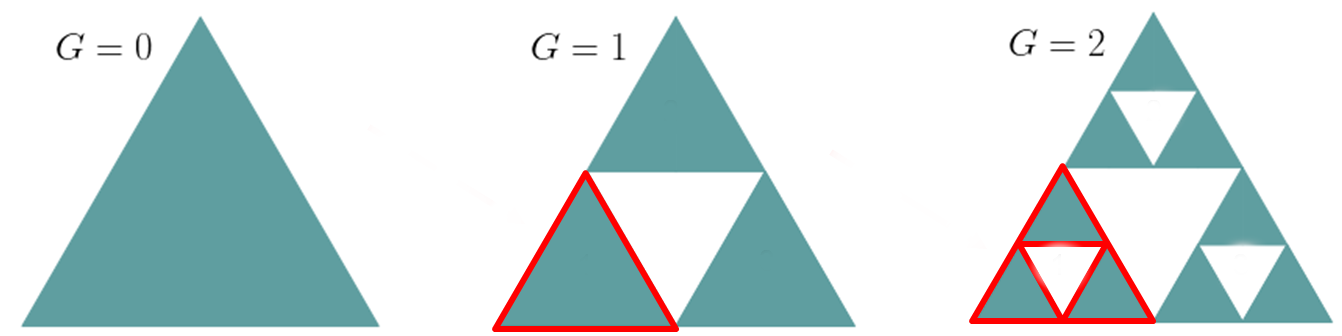
Besides sometimes having a non-integer dimension, fractals have other fascinating properties like self-similarity. Self-similarity means that it does not matter how much you zoom in on an object; you see the same structure repeating over and over again. This property, which is related to the optimization of volume per area ratio, makes fractals actually quite common in Nature. They arise in Romanesco broccoli [1], river networks [2], and pulmonary vessels [3], for example. Intriguingly, our brain is folded in a fractal manner [4], and the patterns that appear close to a phase transition [5] and in turbulent flows [6] are also fractal. But especially because they are so beautiful, fractals are frequently used in all forms of art, from the ceiling of La Sagrada Família to the Triforce from The Legend of Zelda videogame series. They seem to appear in many places, from art to Nature…
...but not in real materials...
Despite their omnipresence, fractals do not often arise in solid materials. Most of the materials are made of a periodic arrangement of atoms, to minimize their energy. However, the forces involved are usually something that tends to pack atoms in a way to optimize their volume, not their area. This means that, although you can find fractals in molecules [7], atoms usually do not organize themselves in a fractal structure to form a solid.
Luckily, scientists do not get discouraged, and if Nature does not give us fractals, we make them by design! This is what a group of physicists and chemists from Utrecht University in the Netherlands, did in 2019: they built a Sierpinski gasket at the nanometer scale, by depositing CO molecules on a surface of copper and manipulating their position with a scanning tunneling microscope [8]. They then showed that the electrons in this material are confined to occupy just a fractal region, and the wavefunction, a characteristic of a quantum state, presents properties that are unique to fractal geometry. This was a fundamental step for the field, and their work was selected as one of the highlights for Nature Physics 15 years [9]. It also motivated a lot of fractal studies in other metamaterial platforms, such as photonic, phononic, and acoustic, but the realization of fractals remained at the design level…
...until now!
This changed in 2021, when a group of physicists from Shanghai Jiao Tong University in China used molecular beam epitaxy to grow Bismuth samples, and found the spontaneous formation of Sierpinski triangles made of a single-layer of Bismuth [10].
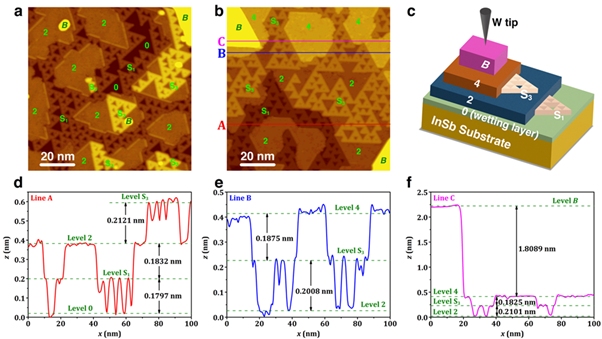
(a,b) Topography of Sierpinski triangle Bismuth films on top of an InSb substrate. (c) Schematic for different island height levels corresponding to the labels in (a,b). (d,e,f) Height profiles for red, blue, and pink lines A, B, and C in (b), respectively. Image from Ref. [10].
The reason for getting Bismuth shaped as a fractal was the substrate: indium antimonide (InSb). When placed on top of InSb, physical stress and chemical bonds favor the formation of angles, and the perimeter (not only area) needs to be optimized. The discovery of this material was another breakthrough in the field, as we now have the means to create real materials with fractal structure that exhibit non-integer dimensions and self-similarity. Moreover, Bismuth atoms have a very remarkable property: they are very heavy atoms and, consequently, have a strong spin-orbit coupling. The spin-orbit coupling acts like an artificial magnetic field that is intrinsic to a material and opens the door to new phenomena in fractal structures: topologically protected states.
Topology enters the fractal stage
Topology is the field of math that studies smooth deformations. In particular, geometric topology considers properties of surfaces that do not depend on the details of these surfaces but rather on their global properties, like the number of holes (also called genus) of a surface. In this sense, for a topologist, a mug is equivalent to a donut since both have one hole, while they are topologically distinct from a sphere that does not have any hole.
Not only is topology useful in math but also in physics. It revolutionized our way of thinking about the properties of phases of matter (and the transitions between them). In these topological phases of matter, the global properties of a material are characterized by something called a topological invariant, which is a number, like the genus of a surface, that completely characterizes a phase of matter. One of the most interesting properties of topological materials is that this topological invariant is related to a very robust feature of a material, in the same way you cannot change the number of holes in a surface without tearing it apart. One of the hallmarks of these robust quantities is the quantization of the conductance in the quantum Hall effect [11, 12], which is so precise that it was used to redefine the kilogram [13]. This quantized response is due to the presence of states on the surface of these materials. These surface states are also very promising for applications, being a route to more efficient transport of information in spintronics [14] and as topological qubits in topological superconductors [15]. After the last decades of research in these materials, physicists now understand some useful components for obtaining these states. One of them is spin-orbit coupling, a relativistic effect that is present especially in very heavy elements like Bismuth!
Therefore, we wondered whether the Bismuth fractals would present any signature of topological states. We then experimentally investigated fractal flakes using scanning tunneling spectroscopy, and found states at very low energies localized either at their vertices or edges.
To understand whether these states are caused by spin-orbit coupling or not, we performed numerical simulations of the fractal using two methods: one is called the muffin-tin, and the other is the tight-binding approach. One approximates a material by a gas of free electrons confined to a fractal structure by repulsive potentials. The other imagines that the electrons are heavily bound to the atomic sites but can tunnel (or hop) between them. Both show the same conclusion: these states only appear in the presence of spin-orbit coupling, thus confirming their topological character. Moreover, we can exactly predict the sequence in which these states appear in these materials, indicating that we understand their behavior quite well. In addition, with the simulations we showed that these states are quite resilient to disorder: we can almost destroy the structure where they are defined, and they still remain there. This robustness further confirms that they have a topological origin.
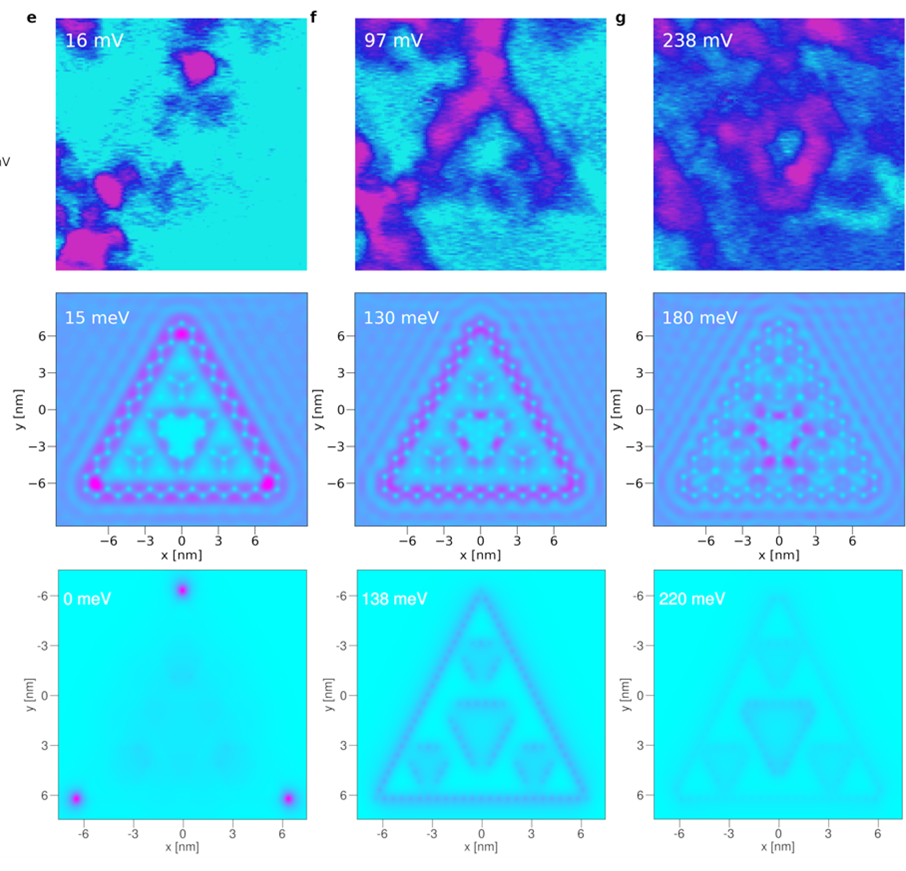
Electronic states observed for Bismuth on top of InSb. The energies in the top left corner indicate the bias voltage. The left figure shows corner states (the bottom right state is missing due to disorder), and the middle and right figures show outer and inner edge states, respectively. Comparison between the experiments (top), muffin-tin (middle), and tight-binding (bottom) density of states of corner and edge states.
Introducing a bit of disorder also makes our theory close to experiments: indeed, by adding a sharp edge to the system, which does not respect the symmetries of the arrangement of the atoms inside the triangle, introduces asymmetries in our simulations that match very well what is observed in the real material.
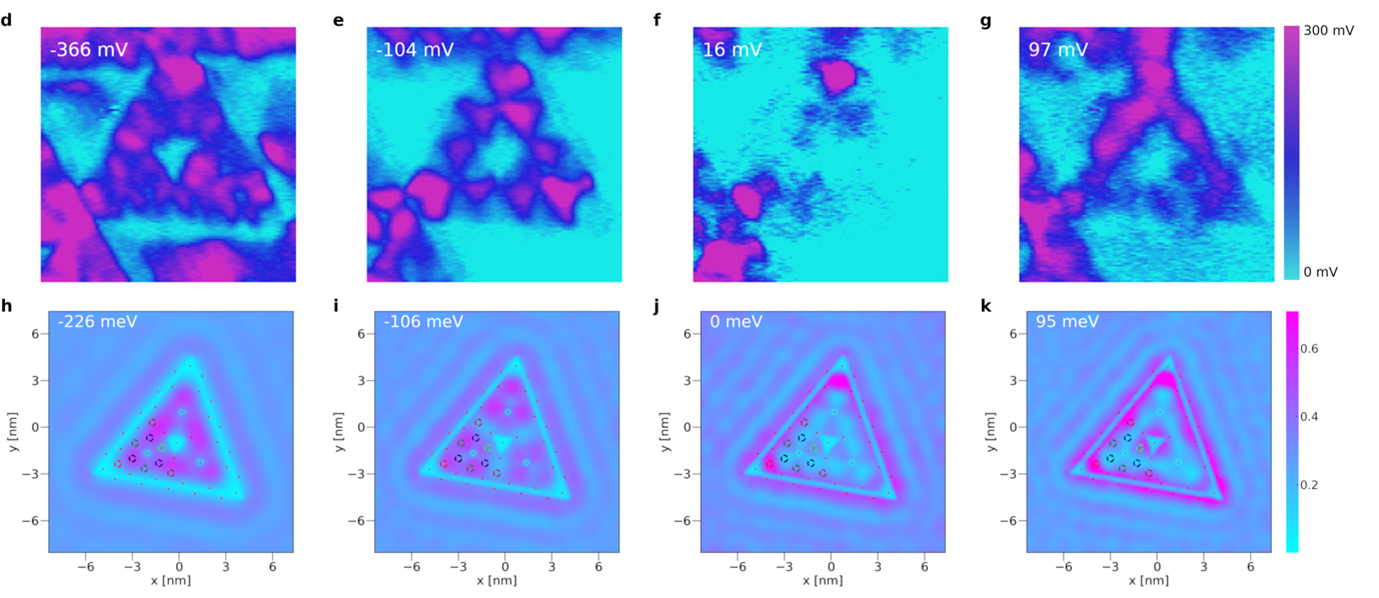
This opens the door for realizing these topological properties in real materials, which have the potential for very interesting technological applications. In fact, these fractals present a high perimeter-to-area ratio, meaning we have more boundary states that can be used for the wonderful applications of topological matter. Our work has revealed the first topological fractal in a real material, and has answered some questions, but there are many more open questions and games to be played at this fractal stage.
References:
[1] Azpeitia et al, Science 373, 192 (2021).
[2] G. Tarboton, et al., WaterResour. Res. 24, 1317 (1988).
[3] J. B. Bassingthwaighte, Acta stereologica 11.Suppl 1 305 (1992).
[4] B. Mota and S. Herculano-Houzel, Science 349, 74 (2015).
[5] S. Liu et al, PRL 116, 036401 (2016).
[6] G. Parisi and U. Frisch, Turbulence and predictability in geophysical fluid dynamics and climate dynamics, Proceed. Intern. School of Physics ’E. Fermi’, Eds. M. Ghil, R. Benzi e G. Parisi, North Holland, Amsterdam (1985).
[7] Shang et al, Nature Chemistry 7, 389 (2015).
[8] S. N. Kempkes, et al., Nat. Phys. 15, 127 (2019).
[9] A. Wright, et al., Nat. Phys. 16, 999 (2020).
[10] C. Liu, et al., Phys. Rev. Lett. 126, 176102 (2021).
[11] K. v. Klitzing, G. Dorda, and M. Pepper, Phys. Rev. Lett. 45, 494 (1980).
[12] J. Thouless, et al., Phys. Rev. Lett. 49, 405 (1982).
[13] How a physics Nobel prize led to the redefinition of the kilogramme, Lindau meeting blog.
[14] D. Pesin and A. H. MacDonald, Nat. Materials 11, 409–416 (2012).
[15] S. Das Sarma, M. Freedman, and C. Nayak, npj Quantum Inf. 1, 15001 (2015).
Follow the Topic
-
Nature Physics

This journal publishes papers of the highest quality and significance in all areas of physics, pure and applied.


Please sign in or register for FREE
If you are a registered user on Research Communities by Springer Nature, please sign in
Would never have thought that The Legend of Zelda would ever be mentioned in this context :D
When I saw my first talk about fractals in condensed matter physics, the first thing I thought about was a Triforce :)