My fluid is more viscous than yours

In simple terms, viscosity is the resistance of a fluid to flow. It reflects how thick a fluid is and how much internal friction exists between its moving layers.

To grasp the idea, just let a liquid fall. Compare honey, a high-viscosity fluid, with water, a low-viscosity one, you’ll immediately see the difference.

Willing to compete for the most viscous fluid ever measured?

As Heraclitus once said, “Everything flows”. Yes, Heraclitus, everything does, but how long must we wait to see it? That’s precisely what viscosity determines. If you don’t believe it, take a look at the world’s longest-running laboratory experiment: the pitch drop experiment. There, a drop of pitch, a substance about two million times more viscous than honey (or twenty billion times more viscous than water), takes over a decade to fall. Too impatient to wait? Check the “Pitch Drop Time Lapse” below and see centuries of patience compressed into minutes. 

History class: on the shoulders of the giants

Humans have known about viscosity for millennia. Around 1600 BCE, the Egyptian scientist Amenemhet had to correct water clocks for temperature-induced viscosity changes, an early, hands-on lesson in rheology, the science of flow.

The first theoretical treatment, however, came much later. In 1687, Isaac Newton formalized the concept of viscosity in his Principia, laying the foundation for modern fluid mechanics. Two centuries later, Navier and Stokes incorporated it into the celebrated Navier–Stokes equations, which remain the cornerstone of fluid dynamics today.

In a gas, the mechanisms behind viscosity are simple

Despite viscosity being almost as old as civilization itself, and relatively simple to measure, its true origin and predictability remain deep physical questions.

Let’s take a step back. Fluids are usually classified as gases or liquids. While this division is not as straightforward as it sounds, the physics of dilute fluids (gas-like) is fairly simple and can be captured by a pinball analogy: particles flying around and occasionally bumping into each other (as shown in Figure 2). In more formal terms, this is the realm of kinetic theory, developed by Maxwell (yes, the same one famous for light) and other physicists during the 18th and 19th centuries.

In this regime, viscosity arises from collisions between atoms and molecules, each moving thanks to their thermal energy. Neglecting interactions and applying a few approximations, one can quickly show that the viscosity of a gas depends on two main quantities: the mean free path (the average distance between collisions) and the average thermal velocity. A few lines of algebra later, you find that gas viscosity increases with temperature, roughly following the square root of temperature.

In short, gases are simple. Boring, in fact. Their behavior is dominated by kinetic energy, with little contribution from intermolecular forces. It’s like going to a party with just a few people, you are bumping into each other, but not much more happens.

The origins of flow in liquids

Liquids are far more exciting, which, for a physicist, usually means we don’t fully understand them. Unlike gases, liquids are dense, strongly interacting, and their particles wander far from their initial positions (unlike in solids, where atoms mostly vibrate around fixed sites). This messy situation is often described as the absence of a small parameter, a theorist’s worst nightmare.

In liquids, viscosity defies the simple rules of kinetic theory: it does not increase with temperature. Try the experiment yourself: pour honey, then put it in the fridge and pour again. Which flows faster? The cold honey, obviously, takes its time. That’s viscosity increasing as temperature drops.

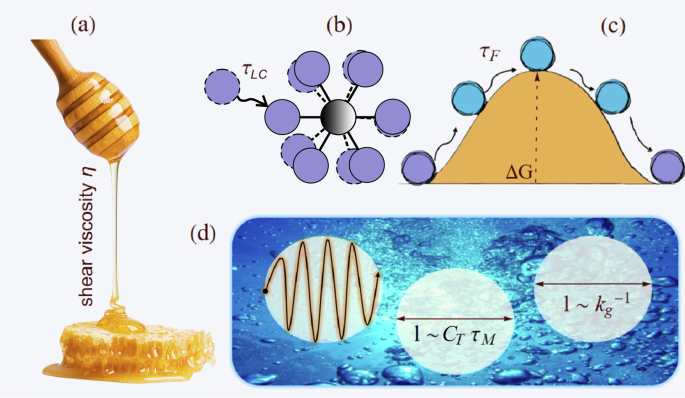
Understanding liquid viscosity means understanding how liquids flow. Why doesn’t an ideal solid flow? Because its atoms can only perform small vibrations around equilibrium, like dancers stuck in one spot. Solids are held together by springs; liquids aren’t. In a liquid, atoms still vibrate like in a solid, but occasionally undergo structural rearrangements, jumping to new positions. These rearrangements are what give rise to flow (see Figure 3).

This dual behavior, solid-like vibrations interrupted by sudden rearrangements, lies at the heart of the Maxwell–Frenkel theory of liquid dynamics, a cornerstone in our modern understanding of how liquids move, deform, and resist.

Liquid viscosity, what we know 

As already mentioned, viscosity in liquid-like fluids is intimately tied to their ability to flow. In contrast, ideal solids do not flow and thus have a nominally infinite viscosity. This immediately suggests that a longer average rearrangement time (τ_F) corresponds to a higher viscosity. From a microscopic perspective, these rearrangements occur when atoms jump over potential barriers formed by their surrounding neighbors. As temperature increases, atoms gain more energy, making these jumps more frequent, resulting in a smaller τ_F and, consequently, a lower viscosity η.

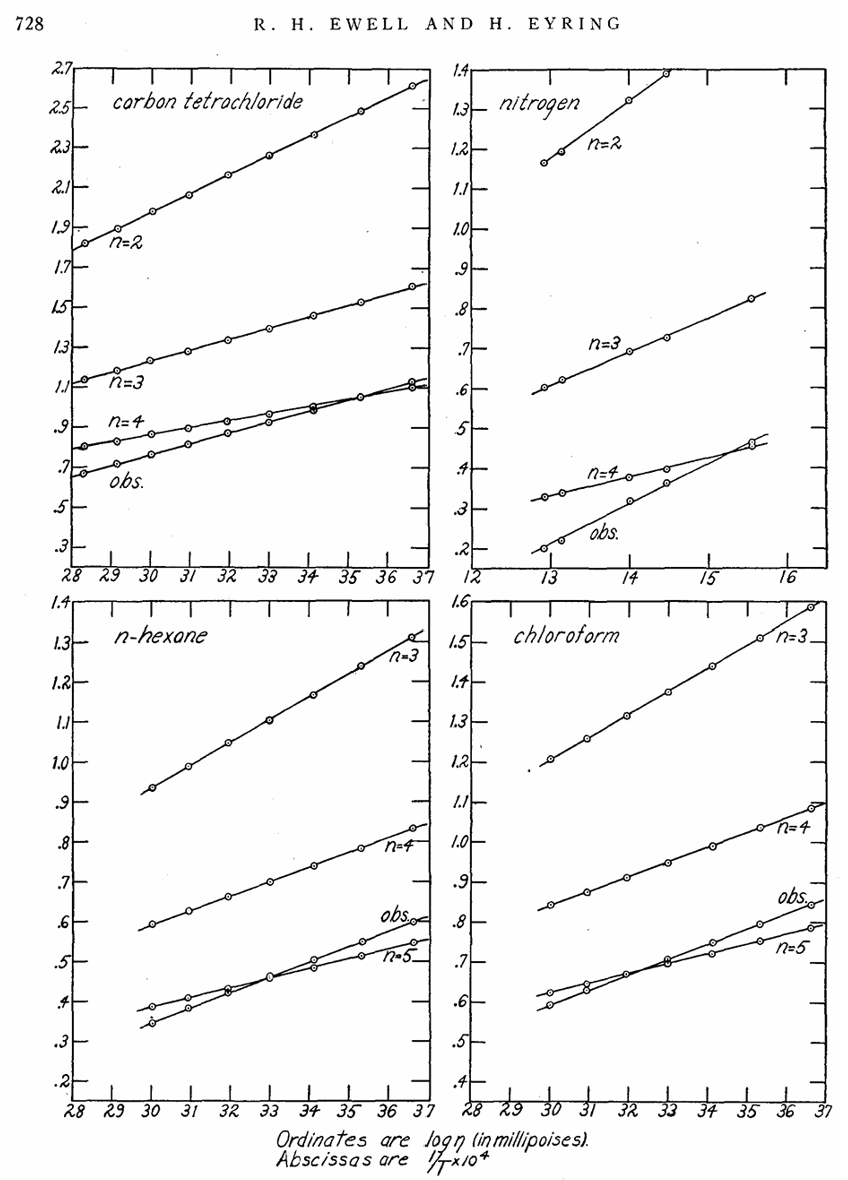
More precisely, such barrier crossings are thermally activated processes with a probability proportional to exp(−ΔG/T), where U is the energy barrier that an atom must overcome to escape its local cage. This simple argument leads directly to the famous Eyring equation for viscosity, η=A exp(ΔG/T), which remains one of the most widely used and elegant formulations to describe liquid viscosity. However, despite its beauty and success (see Figure 4), this formula hides a practical frustration: we have no reliable way to determine the pre-factor A or the activation energy ΔG from first principles.

Other influential frameworks, such as the Green–Kubo formalism and the Born–Green theory, relate viscosity to fluctuations of the shear stress and the underlying interparticle potentials. While powerful, these approaches still fail to reveal the atomistic dynamics responsible for viscous behavior. The current situation thus leaves a fundamental gap in our understanding: how the microscopic motion of atoms in a dense liquid gives rise to the macroscopic flow and viscosity that we can so easily observe with the naked eye, just by watching a drop fall.

Atomic dances behind fluid viscosity

Frenkel was arguably the physicist who came closest to solving this problem. By simplifying atomic motion in liquids as vibrations interrupted by jumps (Fig. 3), he derived an elegant expression for viscosity that, in two dimensions, reads as

η=(k_BT τ_F )/(π ξ²) ​​.

Here, τ_F​ is the average time between atomic jumps, and ξ is the distance separating the initial and final positions of a jumping atom. This is precisely where our collaboration with Dong, Shaoyu, Chen, and Yan began, hopping back and forth between Shanghai and Suzhou, two neighboring Chinese cities laced with canals and rivers, offering no shortage of inspiration for people obsessed with fluids and flow.

Inspired by Frenkel’s ideas, our initial goal was to make his approach more predictive by identifying, from first principles, the microscopic time and length scales (τ_F and ξ) appearing in his formula and giving them a measurable definition that could be extracted from simulations, or even experiments.

As physicists often do, we started with simplifying assumptions, the classic “spherical cow” mindset. First, we assumed that the length scale between two jumps is largely governed by the liquid’s density and roughly corresponds to the interparticle distance, the space available for one atom to move into another’s place. Crude, perhaps, but surprisingly reasonable in dense systems.

The next challenge was defining τ_F​. Here, we built upon Egami’s seminal ideas on local atomic connectivity. We identified Frenkel’s time with the lifetime of local atomic connectivity, τ_LC​, that is, the average time before an atom gains or loses a neighbor. In other words, we assumed that the process of making and losing friends (Figure 5), at the atomic scale, holds the key to understanding viscosity in liquids. This process can be directly visualized in molecular dynamics simulations as demonstrated in the video below, where each neighbor of the red particle is colored in blue and tracked over time.

After a few manipulations, and following the assumptions described above, we arrived at a remarkably simple expression for the viscosity of a two-dimensional liquid-like fluid:

η=ρ v_p² τ_LC​,

where v_p​ is the average thermal speed of the particles and ρ the mass density. Simple, isn’t it?

To be precise, the formula also includes a dimensionless numerical factor of order one, reflecting the uncertainty in identifying the jump length scale ξ with the interparticle spacing. Yet, physical reasoning suggested this factor should be close to unity, so do not overthink it.

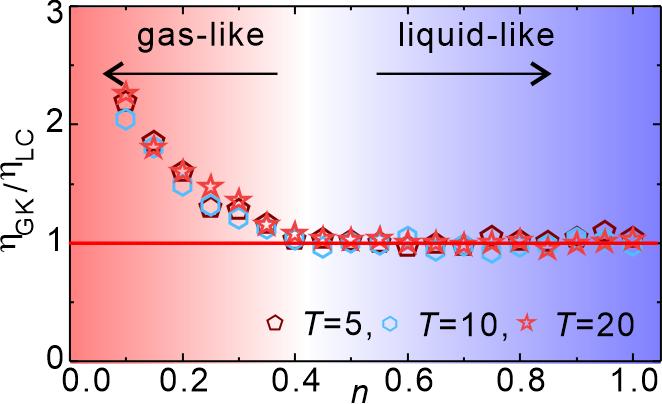
The final and perhaps most important step was to test our prediction. We turned to molecular dynamics simulations of three different fluids with distinct interparticle interactions. To our delight, we had our own little Eureka moment: the results showed excellent agreement between our theoretical prediction and the numerical data. The supposedly “order-one” factor turned out to be indeed very close to one for all simulated liquids.

Figure 6 illustrates this success by comparing viscosities obtained via the Green–Kubo formalism (η_GK) and our theoretical expression (η_LC). The two match closely across the entire liquid-like regime. As expected, our model fails in the gas-like regime, but that’s hardly a disappointment, since kinetic theory already works perfectly there.

In essence, the lifetime of local connectivity (τ_LC​) emerges as the key microscopic descriptor of viscosity. It connects naturally to classical frameworks such as the Eyring equation, and its associated length scale ties directly to the macroscopic behavior of shear excitations in liquids.

But I won’t spoil all the fun here, those details are in the paper. Consider this just the trailer; the real story unfolds in the full version.

The takeaway from our experience is this: never underestimate the systems around us that seem simple or innocuous, they often conceal a whole universe of fascinating and unresolved questions. As scientists, we should be most intrigued by the phenomena visible to the naked eye, without the need for telescopes or microscopes. These are the systems that can truly spark the imagination and unsettle a curious mind.

In Italy, there's a saying: “Non perderti in un bicchiere d’acqua”, a warning not to get lost in trivial problems. But after this journey, I’ve come to believe that the saying gets it wrong. Water, and fluids in general, are anything but trivial. They are neither simple nor boring.