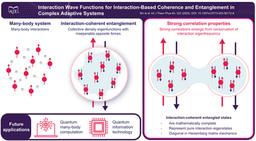
Quantum entanglement, famously exemplified by the Einstein-Podolsky-Rosen (EPR) paradox, is often described as "spooky action at a distance" [1, 2]. This phrase highlights the extraordinary correlation and instantaneous mutual influence between two entangled components, A and B, even when separated by vast distances. In such cases, a change in one part (A or B) leads to an immediate adjustment in the other, enabling both to dynamically adapt and self-organize to maintain their entangled state. This seemingly intelligent and coordinated behavior among non-living particles or photons has long remained mysterious, fueling debate and inquiry in the scientific community for nearly a century.

Although quantum coherent entanglement was observed through optical interference experiments in 1991 [3, 4], the precise mechanism behind the phenomenon has remained elusive. In a breakthrough study, a research team led by Mr. Leilei Shi at the University of Science and Technology of China (USTC) in Hefei, Anhui, has reported the discovery of the mechanism behind what they term Bessel eigenstates. Their research reveals how these states underpin the strong correlations between entangled components, regardless of spatial separation. Notably, this interdisciplinary study draws upon concepts from quantum science, financial theory, and complexity science. The team's findings are detailed in their paper, “Interaction Wave Functions for Interaction-Based Coherence and Entanglement in Complex Adaptive Systems,” published in the International Journal of Theoretical Physics, a Springer Nature journal [5].

Reference

1. Einstein, Albert, Boris Podolsky, and Nathan Rosen (1935): “Can Quantum-Mechanical Description of Physical Reality Be Considered Complete?” Physical Review, 47 (May 15), 777–780.
2. Schrödinger, Erwin (1935): “Discussion of Probability Relations between Separated Systems,” Mathematical Proceedings of the Cambridge Philosophical Society, 31(4), 555-563.
3. Zou, Xing-Yu, Li-Jun Wang, and Leonard Mandel (1991): “Induced Coherence and Indistinguishability in Optical Interference,” Physical Review Letters, 67(3), 318-321.
4. Wang, Li-Jun (Lijun), Xing-Yu Zou, and Leonard Mandel (1991): “Induced Coherence without Induced Emission,” Physical Review A, 44(7), 4614-4622.
5. Shi, Leilei, Xinshuai Guo, Wei Zhang, and Bing-Hong Wang (2025): “Interaction Wave Functions for Interaction-Based Coherence and Entanglement in Complex Adaptive Systems,” International Journal of Theoretical Physics, 64 (12), 323. https://doi.org/10.1007/s10773-025-06172-6