Spin glasses are disordered magnets characterized by conflicting, randomly interacting elements. Determining their ground states is significant for gaining insight into disordered magnets and solving various challenging combinatorial problems. Despite its significance, finding the ground states of spin glasses has proven difficult due to its NP-hard nature, meaning that using exact algorithms with polynomial time complexity has been a challenge.

Our recent research, published in Nature Communications, has led to the development of a deep reinforcement learning (DRL) framework called DIRAC. This framework has the ability to calculate spin glass ground states efficiently and directly. The advantages of DIRAC are numerous. To begin with, it outperforms existing thermal annealing methods in terms of accuracy. Additionally, it offers better scalability compared to other methods. Finally, DIRAC can be utilized to improve thermal annealing techniques, providing even better solutions.

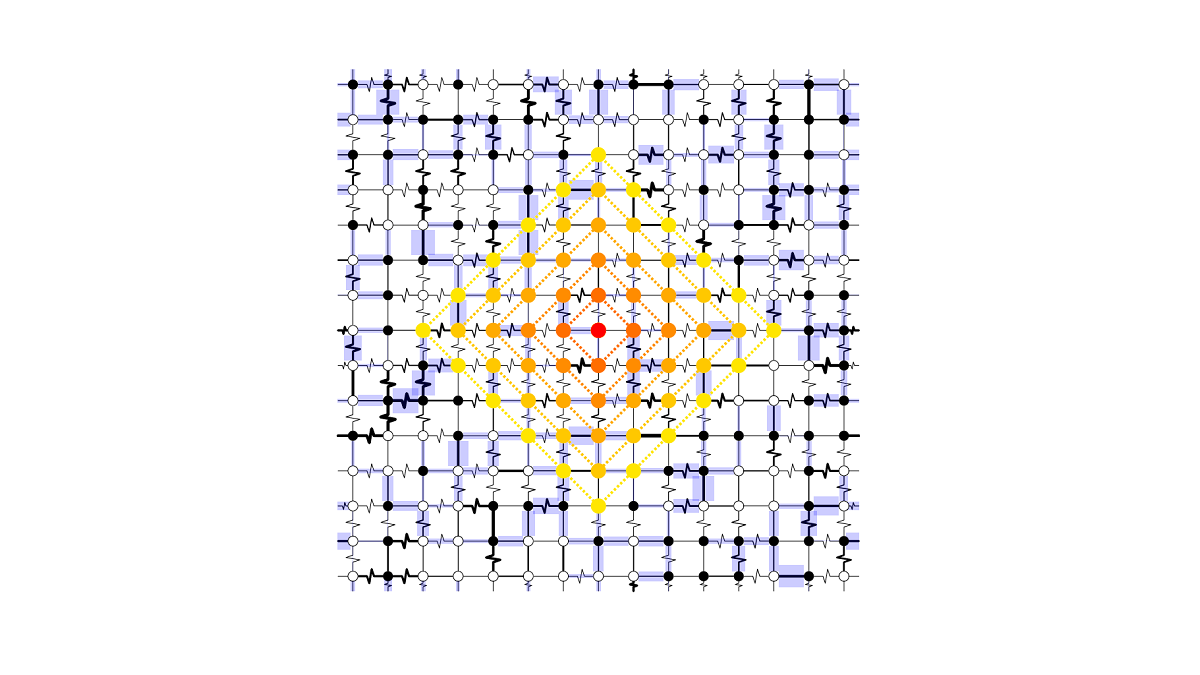
The design of the DIRAC agent is based on the "Encoder-Decoder" framework. A graph neural network (GNN) is utilized to encode the lattice structure and spin glasses by repeating multiple iterations of message-passing, thereby capturing the long-range interactions between spins. During each iteration, the encoder performs edge-update and node-update operations consecutively. The decoder, which is a classical multilayer perceptron (MLP) with ReLU activation, uses the representations from the encoder to calculate a long-term gain prediction for each spin flip. The learnable parameters are updated using the n-step Q-learning algorithm.

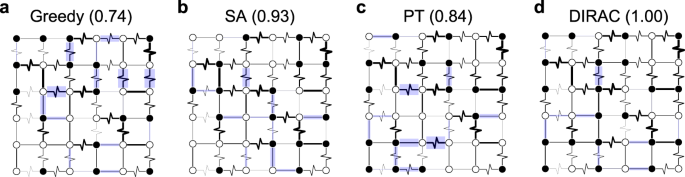
DIRAC was trained using small-scale spin glass instances and can be applied to larger ones. The technique of gauge transformation in Ising systems was employed during application, and several effective strategies were designed to search for spin glass ground states, including DIRAC^1, DIRAC^m, and DIRAC-enhanced annealing algorithms like DIRAC-SA and DIRAC-PT.

The results of our experiments have revealed several important and interesting findings. Firstly, for small Ising systems whose exact ground states can be calculated within an acceptable time, we found that DIRAC was able to find the ground states faster than other competitive baseline methods. Secondly, for large Ising systems where the exact ground states cannot be confirmed within an acceptable time, we found that DIRAC always achieved the lowest energy with the same number of initial configurations as the competition. Finally, an analysis of DIRAC's superior performance shows that it mimics human intelligence in solving the ground state problem. When faced with spin glass ground states, it learns to prioritize long-term gains over short-term satisfaction. With the anti-ferromagnetic Ising model, it exhibits remarkable foresight by making smart moves each time.

Moreover, we evaluate DIRAC's exceptional performances across a range of scenarios including varying coupling distributions (Gaussian, Bimodal, and Uniform), topological structures (trees, loopy trees, and lattices), difficulty levels, and spin glass models (Edwards-Anderson and Sherrington-Kirkpatrick).

Not only is DIRAC highly effective, it is also computationally efficient with better scalability than other methods. Additionally, DIRAC can be easily accelerated with a GPU, unlike other methods.

Multiple studies have demonstrated that numerous NP-hard problems can be expressed through Ising formulations. As such, we applied DIRAC to solve the max-cut problem, a well-known example of the mapping between Ising spin glasses and NP-hard problems, and found that DIRAC consistently outperforms other max-cut solvers.

In the future, advancements in deep graph representation may lead to the design of a more effective encoder, and the development of reinforcement learning techniques may enhance the training process. These advancements have the potential to further improve DIRAC's performance in finding the ground states of Ising spin glasses. The utilization of gauge transformation in DIRAC and the integration of DIRAC with annealing-based methods may also inspire other physics-guided AI research. Our current framework is only the beginning of this exciting journey.