Enhancing sensitivity and precision necessarily entails more frequent jumps
Published in Physics, Protocols & Methods, and Mathematics

Background and motivation
Nonequilibrium physical systems and stochastic thermodynamics
The second law of thermodynamics states that the total entropy of an isolated macroscopic system never decreases with time. In reality, most systems are subjected to significant fluctuations and dissipation so they are generally out of equilibrium such as nanomachines or biochemical systems. For such situations, the usual framework of equilibrium thermodynamics becomes inapplicable. Over the last three decades, stochastic thermodynamics has been greatly developed to provide a general framework for understanding dissipation and thermal fluctuations far from equilibrium.
Thermodynamic uncertainty relations and kinetic uncertainty relations
Recently, a rigorous result known as the thermodynamic uncertainty relation (TUR) was discovered within the stochastic thermodynamics framework, which dictates that for a nonequilibrium Markovian jump process the precision of a nonequilibrium current observable J (heat current or charge current, etc) be bounded from below by the thermodynamic dissipation characterized by the entropy production (EP) σ.
However, it was realized that the dissipation alone may not be adequate to bound the fluctuations of the system fully. For far-from-equilibrium systems, a key non-dissipative metric found in this context is the dynamical activity (DA), which represents the frequency of state transitions occurring in a stochastic process thus characterizing the kinetics. In parallel to the TUR, it has been proved that the precision of a current is also bounded by the kinetic uncertainty relation (KUR).
Response thermodynamic uncertainty relation and our motivation
Concurrently, the development of finding fundamental principles characterizing nonequilibrium systems' static response to external perturbations is also prosperous, apart from the seminal fluctuation-dissipation relation. Figure 1 depicts a schematic illustration of a time-integrated current subjected to a perturbation in a control parameter θ of the system. Notably, a response thermodynamic uncertainty relation (R-TUR) valid for the nonequilibrium steady state of a time-independent Markov jump process has been conjectured and then proved very recently [K. Ptaszyński, et al., Phys. Rev.Lett. 133, 227101 (2024)].

A natural and compelling question arises: Does there exist a counterpart of the R-TUR in terms of the DA? In other words, is there a fundamental relationship between the precision of response and the traffic of the nonequilibrium process?
Enhancing sensitivity and precision necessarily entails more frequent jumps
Our main result -- response kinetic uncertainty relation
We answer the above question by establishing a rigorous response kinetic uncertainty relation (R-KUR) -- a trade-off between the precision of response of generic observables to arbitrary perturbations and the DA as a complementary but more general counterpart of the R-TUR. It tells us that enhancing sensitivity and precision necessarily entails more frequent jumps; alternatively, for a given stochastic dynamics (fixed frequency of transitions), high sensitivity to the change in a control parameter implies large fluctuations or low precision.
In comparison with the R-TUR which applies only to the steady state of a time-independent Markovian process and to a current-type observable, our R-KUR can be applied to arbitrary Markov jump processes and does not necessitate perturbations to the driving speed or observation time, making it more versatile in applications. We also note that the R-KUR is valid for any process that can be described by the master equation, without being restricted to thermodynamic systems.
Example illustrations
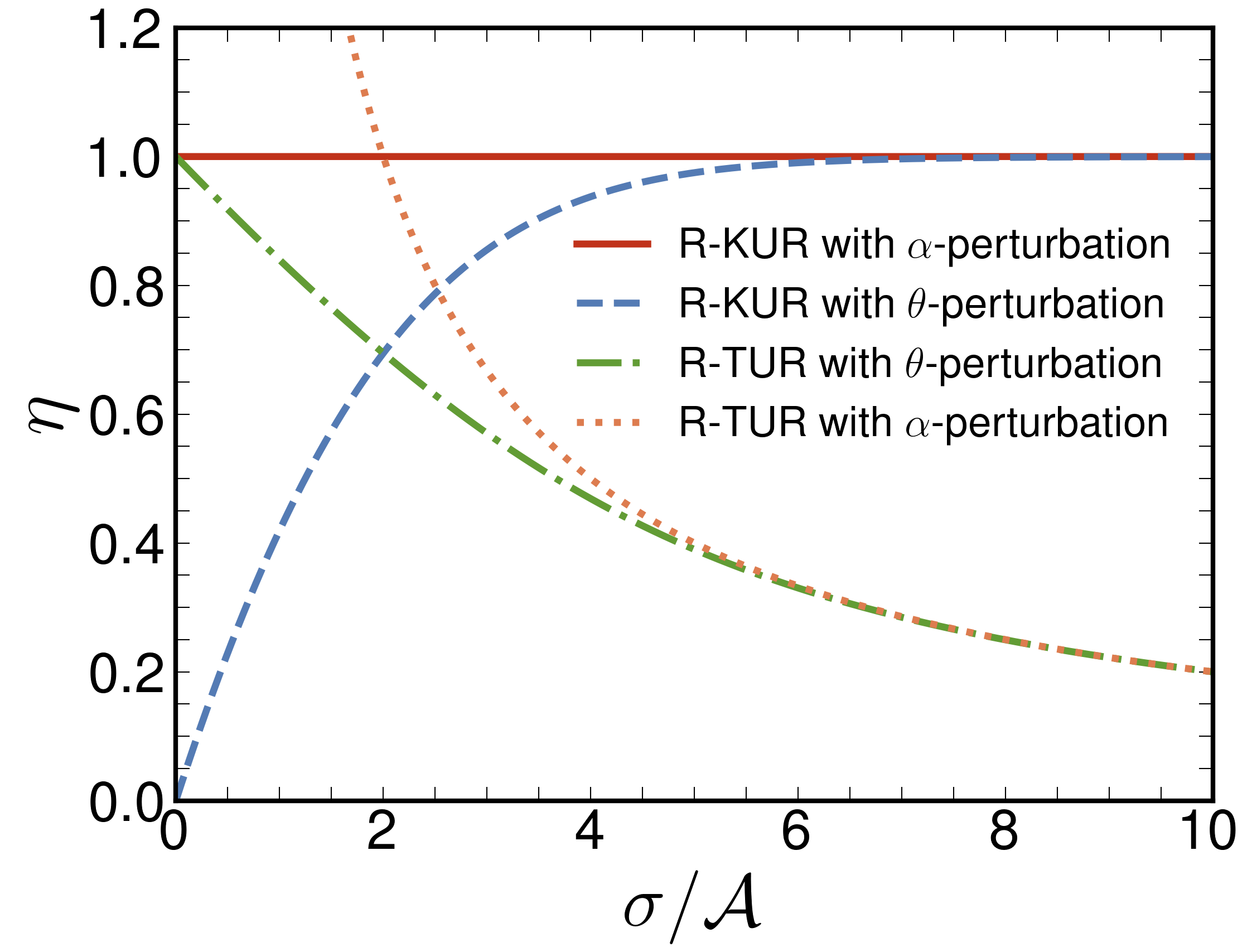
We have examined our R-KUR in two examples. The first one is a one-dimensional biased random walker, which is a successful model describing the dynamics of molecular motors in biosystems, such as the kinesin moving on cytoskeletal polymer microtubules. We examine the efficiency of the bound which should be upper bounded by unity while perturbing the symmetric parameter θ which is required to validate the R-TUR or perturbing the anti-symmetric parameter α which may possibly break the R-TUR. The numerical results are shown in Figure 2. It is clear that our R-KUR always holds but the R-TUR can be broken while perturbing α. Promisingly, the R-KUR with α-perturbation attains equality for all values of the parameters and the R-KUR with θ-perturbation saturates the equality in the far-from-equilibrium regime characterized by a large dissipation-activity ratio. The second example is referred to in our article.
Conclusion and outlook
The broad applicability of our R-KUR underscores its potential applications ranging from biochemical processes (e.g., biochemical sensing, switching, and molecular motors) to engineered nanostructures operating away from equilibrium. A feature of our results is that all involved quantities can be measured experimentally from the statistics of stochastic jumps. It is worth mentioning that the measurement of DA can sometimes be more accessible than that of EP, as the latter requires distinguishing the direction of jumps. Candidates for physical implementation that allow stochastic trajectories to be tracked with a high resolution include a single defect center in diamond, single-electron boxes at low temperatures, molecular motors, NMR setups, nanoscale electronic conductors, and superconducting NISQ quantum processors, etc.
Our R-KUR demonstrates a fundamental trade-off between sensitivity and precision in stochastic systems. For a fixed number of transitions, high sensitivity implies large fluctuations or low precision. This is apparently similar to the behavior of a thermodynamic system in the vicinity of a critical point where the susceptibility is extremely large and the fluctuations of the order parameter are also significant. On the other hand, due to the intimate relationship between the DA and the nonequilibrium critical phenomena exploring any potential connections between the R-KUR and thermodynamic phase transitions holds promise for intriguing investigations.
Follow the Topic
-
Communications Physics

An open access journal from Nature Portfolio publishing high-quality research, reviews and commentary in all areas of the physical sciences.
Related Collections
With Collections, you can get published faster and increase your visibility.
Higher-order interaction networks 2024
Publishing Model: Open Access
Deadline: Feb 28, 2026
Non-Markovian quantum dynamics in physical systems: description and control
Publishing Model: Open Access
Deadline: Dec 31, 2025





Please sign in or register for FREE
If you are a registered user on Research Communities by Springer Nature, please sign in