How does Nernst effect probe strange metals?
Published in Physics

Named after its discoverer Walther Nernst [1], one of the most prominent physicists in the early twentieth century, the Nernst effect has been recognized as an important thermoelectric effect particularly useful in fundamental research. Its relation to the Seebeck effect, discovered more than six decades earlier by Thomas Johann Seebeck, is analogous to that of the electric Hall effect to the ordinary electrical conductivity.
As the name ‘thermoelectricity’ suggests, one needs a system with mobile charge carriers to establish a thermoelectric effect. The schematics in Fig. 1 illustrate the principle of the thermoelectric effects. The basics of the thermoelectric effect can be analyzed by considering the total electric current density , in the language of conductivity tensors. Namely,
![]()
where σ and α are the electric and thermoelectric (or Peltier) tensors, -∇T is the applied thermal gradient (the minus sign is purely a matter of convention), and E is the electric field (applied or generated or both). More intuitively, the thermal gradient generates a thermal force on the mobile carriers and leads to the accumulation of carriers on the cooler end, which, in the open circuit boundary condition (J = 0), leads to an electric field E counterbalancing further charge accumulation. The quantity S = Ex/(-∇T) is the Seebeck coefficient, also known as thermopower; it may have either sign.
Like the Hall effect, the Nernst effect requires a magnetic field (or a spontaneous magnetization) to start with. In this case, the conductivity tensors have nonzero off-diagonal components. The Lorentz deflection of the Seebeck electric field leads to a conventional Hall component σyxEx, counterbalanced by an opposite Peltier component αyx(-∇xT). Again, the open circuit boundary condition leads to a Nernst signal N = -S tanθH+αxy/σxx, where tanθH = σxy/σxx is the Hall angle (which is usually proportional to the z-component of the magnetic field B). Since this quantity is typically much smaller than 1, and moreover in most metals there is a near-exact cancellation (the "Sondheimer cancellation" [2, 3]) between the conventional Hall term and the Peltier term, the magnitude of the Nernst coefficient ν ≡ N/B is typically more than one order of magnitude smaller than the Seebeck coefficient in conventional metals. A series of elegant works by the pioneer in the field Kamran Behnia [4-6] showed that the Nernst coefficient in a wide range of metals obeys a simple relation, which is
![]()
The scale of the Nernst coefficient is set by the combination of natural constants (π2/3) (kB/e) ≈ 283 μVK-1, and two material-specific quantities: the mobility μH and Fermi energy EF. The smallness of the Nernst coefficient relative to this quantity originates from the large Fermi energy and low mobility. On the other hand, thermodynamic analysis shows that the Nernst signal measures precisely the entropy per mobile charge carrier [5], which is usually inaccessible by other probes.
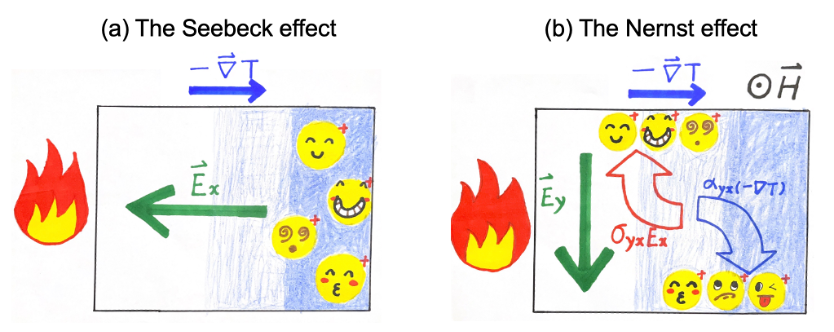
Fig. 1: Schematics illustrate the principle of the thermoelectric effects: (a) The Seebeck effect and (b) The Nernst effect. Yellow balls represent the charge carriers (with hole-like carriers as an example). Green arrows indicate the thermoelectric field. Red and blue arrows indicate the conventional Hall component σyxEx and the Peltier Hall component αyx(-∇xT) and their respective deflection in a magnetic field. The Cartoons were drawn by the author’s two children, who are making their first acquaintance with science in elementary school. The results should of course not be taken too literally; for example, the charge carriers, despite being identical particles as required by quantum mechanics, were sketched with various facial expressions. The author sees no reason to discourage the kids’ fancy imagination. One plausible remedy is to think of the different “faces” as different “phases”; then, it makes better sense as the wavefunctions of the carriers are allowed to carry different phases.
As the mobility μH and Fermi energy EF are accessible experimentally by independent measurements, a variety of materials have been tested using eq. 1 to evaluate the Fermi-liquid Nernst signal. As shown in Fig. 2, eq. 1 is remarkably successful among a large set of materials with mobility and Fermi energy spanning over several decades. This is particularly impressive as the Nernst coefficient in eq. 1 is purely based on a single-band Drude picture (that is, all the carriers on the Fermi surface are described by Bloch wave functions with the same band index), a model that is destined to be oversimplified to account for the various systems. Because of the remarkable success, Eq. 1 has become the benchmark in understanding the Nernst effect in Fermi liquids. Nowadays, it is almost a standard practice to measure the thermoelectric response in a newly discovered metal or metallic phase and compare it with eq. 1. Very often, the agreement was found to be satisfying, which has led to the growing body of data points in Fig. 2. However, when the measured Nernst signal severely deviates from eq. 1, it implies unconventional mechanism beyond the simple Drude transport, which often suggests exciting new possibilities. Our work on the anomalous enhancement of the Nernst effect in strange metals is a typical example of such [7].
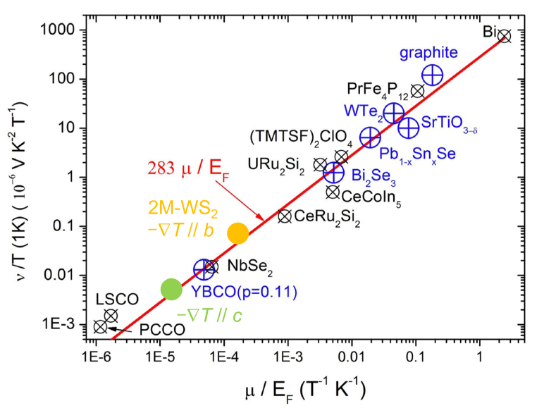
Fig. 2: Figure adopted from the supplementary materials (Fig. S15) in our paper. The magnitude of the low-temperature Nernst coefficients divided by temperature in a variety of metals plotted versus the ratio of mobility to Fermi energy were originally adopted from K. Behnia’s review [5]. The yellow and green solid points are Nernst coefficients of 2M-WS2 along the b and c crystalline directions at 10 K. The low-temperature Nernst signal in the Fermi liquid state of 2M-WS2 follows the typical behavior of Fermi liquid as expected by eq. 1 in the main text.
When Yusen (the first author of our paper) and I first saw the temperature dependence of the Nernst coefficient in the 2M-WS2 (the main material system we focused on in the paper) popping out of our measurement system, it seemed to be a trivial case. The Nernst response showed a broad peak at the intermediate temperature and became very small at low- and high-temperature sides, a general trend expected for any metallic system. However, when we performed the ‘routine’ and plotted it quantitatively against eq. 1, a dramatic enhancement by over one order of magnitude caught our attention (Fig. 3). From that moment, we realized that something unusual had happened.
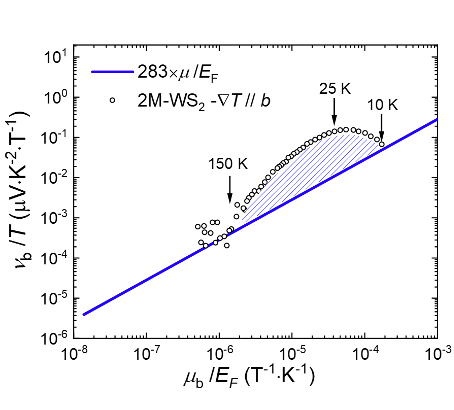
Fig. 3 The Nernst coefficient along the b axis in 2M-WS2 is replotted against μH/EF to show the anomalous enhancement around 25 K.
It took us quite a while trying to figure out what happened behind the strongly enhanced Nernst effect. It was not until a discussion with my theorist friend Wenxin Ding (a coauthor of our paper) when he pointed out the striking resemblance between our resistivity data and his earlier theoretical calculation (though based on a model without considering realistic material parameters), that we began to realize the deep connection between the enhanced Nernst effect and the quasiparticle coherence in the system. The peak temperature in the Nernst signal is precisely the quasiparticle coherence temperature of the system, above which the Fermi liquid quasiparticles are no longer well-defined, and the system enters the strange-metal state. The presence of such an anomalous Nernst response was further verified in other independent strange metals, demonstrating its universality.
An enhanced Nernst signal right at the crossover between a Fermi liquid and a strange metal provides valuable insight into the elusive charge carriers in strange metals, which has been an outstanding problem in modern condensed matter physics. Despite the ubiquity of the strange-metal state in many strongly correlated materials, including the heavily-pursued high-temperature superconductors, people’s knowledge of the strange-metal physics is very limited—even the nature of their charge carriers remains unknown, let alone the underlying mechanism. Our Nernst measurement indicates that a dramatic entropy change of the charge carrier takes place when the carriers transform from quasiparticles in Fermi liquid to the elusive charge carriers in strange metals. Our results place clear experimental constraints on the mechanism of strange metals.
There are certainly many questions to be resolved before we can have a holistic view of strange-metal physics. What is the nature of the carrier scatterings in strange metals? If the Planckian scattering (a scattering rate proportional to kBT/hbar, the highest scattering rate allowed by quantum mechanics [8]; hbar being the reduced Planck’s constant) is confirmed, how do the carriers work collectively to realize such a fast relaxation? With the power of the Nernst effect in probing the entropy of charge carriers, we wish to explore further these exciting problems.
The author is indebted to Prof. Tony Leggett for his generous help and inspiring guidance over the years, and in particular, for spending time to read, correct, and comment on this essay. The author also acknowledges Profs. Qi Liang, Hong Sun, Zhanhai Dong, Feng He, and Shengguang Liu for their comments. Lastly, the author thanks Yueyang Xing and Evan Xing for contributing their hand-drawn schematics in Fig. 1.
References:
- The effect was discovered by Walther Nernst together with Albert von Ettingshausen in 1887, following a suggestion by Ludwig Boltzmann. It is also referred to as the Nernst-Ettingshausen effect. See http://www.nernst.de for more information.
- Sondheimer, E. H. & Wilson, A. H. The theory of the galvanomagnetic and thermomagnetic effects in metals. Proc. R. Soc. A 193, 484–512 (1948).
- Wang, Y. et al. Onset of the vortexlike Nernst signal above Tc in La2-xSrxCuO4 and Bi2Sr2-yLayCuO6. Phys. Rev. B 64, 224519 (2001).
- Behnia, K. The Nernst effect and the boundaries of the Fermi liquid picture. J. Phys. Condens. Matter 21, 113101 (2009).
- Behnia, K. & Aubin, H. Nernst effect in metals and superconductors: a review of concepts and experiments. Rep. Prog. Phys. 79, 046502 (2016).
- Readers interested in a more comprehensive understanding of thermoelectricity are strongly recommended to refer to the book by Kamran Behnia, Behnia, K. Fundamentals of Thermoelectricity (Oxford Univ. Press, 2014).
- Yang, Y., Tao, Q., Fang, Y. et al. Anomalous enhancement of the Nernst effect at the crossover between a Fermi liquid and a strange metal. Nat. Phys. (2023). https://doi.org/10.1038/s41567-022-01904-5.
- For comprehensive reviews on strange metal, please refer to Phillips, Philip W., Hussey, Nigel E. and Abbamonte, Peter, Stranger than metals, Science 377, 169 (2022); Hartnoll, Sean A. & Mackenzie, Andrew P. Colloquium: Planckian dissipation in metals. Rev. Mod. Phys. 94, 041002 (2022).
Follow the Topic
-
Nature Physics

This journal publishes papers of the highest quality and significance in all areas of physics, pure and applied.


Please sign in or register for FREE
If you are a registered user on Research Communities by Springer Nature, please sign in