Recent advances in the areas of parity-time (PT)-symmetry have showed that enhanced sensitivity can be achieved by biasing a sensor system at exceptional points (EPs). The EPs are non-Hermitian degeneracies where both eigenfrequencies and their corresponding eigenvectors merge. Although increased sensitivity has been demonstrated in the EP sensing scheme, it has triggered a controversial debate over fundamental resolution limits and noise enhancement. 

It has known that the nonlinear PT-symmetric inductor–capacitor (LC) system with the gain saturation mechanism can automatically achieve a steady-state oscillation, eliminating the imaginary part of the eigenfrequencies and suppressing the noise. Hence, the nonlinear PT-symmetric LC configurations for the LC sensor have been explored. 

Here, we theoretically propose and experimentally demonstrate enhanced figure of merit (FOM) of LC passive wireless sensors based PT-symmetric configurations of the linear loss and saturable gain. As shown in Fig.1a, it consists of a pair of parallel RLC resonators in which a passive sensor operates as the loss resonator, while parameters to be sensed, i.e., perturbation δ, are exerted on the sensitive capacitor at the loss resonator. To wirelessly interrogate the sensor, a readout circuit composed of –RLC tanks operating as the gain resonator is inductively coupled to the sensor. The gain (–R) is realized by a nonlinear amplifier. The coupling strength is adjusted so that our system is initially located at the exact symmetric phase close to EPs. The proposed sensing scheme shows that the eigenfrequency detuning follows Δƒ=|ƒ-ƒ_EP|∝³√δ , which indicates that the PT-symmetric LC configurations with the linear loss and saturable gain has the cube-root singularity, distinct from  Δƒ∝√δ for the conventional linear counterpart, as shown in Fig.1b.

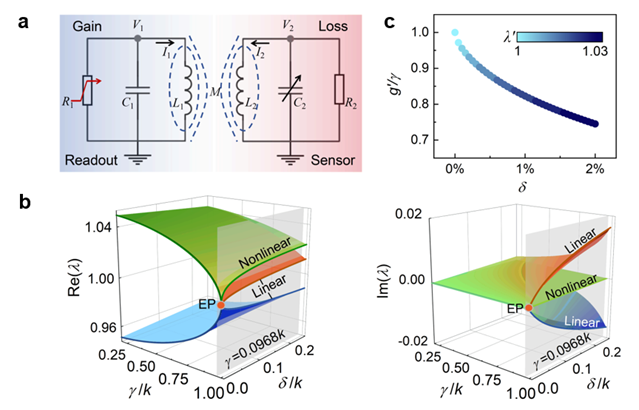
Fig. 1 | LC passive wireless sensors based PT-symmetric configurations of the linear loss and saturable gain.

Nonlinear PT-symmetric theory.

To describe how PT-symmetric LC configurations of the linear loss and saturable gain lead to a cube-root singularity, we develop a model for the PT-symmetric LC resonators shown Fig.1a. The specific derivation process is shown in “Nonlinear PT-symmetric theory” of the article, and we will not describe it in detail here. Based on the hypothesis of real-valued eigenfrequency, the steady-state oscillation eigenfrequency of system can be given as the equation below

λ^'≈1+1/2*(k^2/3 δ^1/3).

It is clear from the equation that the PT-symmetric LC configurations of the linear loss and saturable gain has the cube-root singularity. Not only that, our results also demonstrate that two complex eigenfrequencies have an evident physical meaning discussed in the article, nevertheless, they need further demonstrations.

Experiment setup

To validate the proposed scheme, we built a wireless wearable sensor for temperature monitoring, as shown in Fig. 2. The LC wireless wearable sensor allows for real-time and continuous monitoring without long and laborious steps. The temperature sensing capacitor was implemented here by an interdigital capacitor coated with polyethylene glycol. The temperature sensor as a loss resonator consists of the inductor coil and sensing capacitor fabricated on a fully flexible printed circuit (FPC). The capacitance of the sensing capacitor increases as temperature, leading to a perturbation of 0~2% to the loss side, shown as the green dot curve in Fig. 2a. An inductor coil in a readout circuit is identical with that in the loss side. The inductor coil and discrete variable capacitor as the gain resonator were coupled with the sensor, forming PT-symmetric LC configurations, as shown in Fig. 2b. A negative resistance consisting of an operation amplifier and an adjustable resistor was integrated on the readout circuit board. We tuned the components on the loss and gain side so as to achieve PT-symmetric LC configurations. We then set the nonlinear gain slightly larger than the loss to make the system unstable in the initial state. By precisely adjusting the coupling distance d between the two coils, the system can be operated at the exact phase close to EPs, as shown in Fig. 2c.

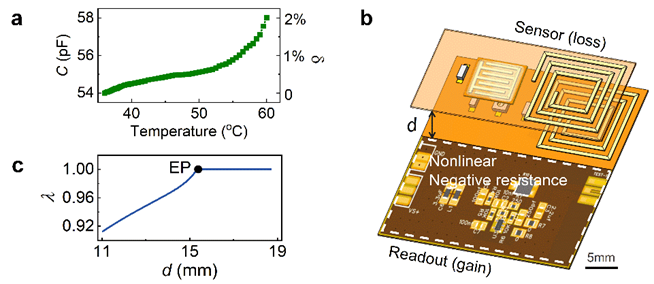
Fig. 2 | Experiments of nonlinear PT-symmetric LC configurations.

Sensitivity enhancement verification.

Fig. 3a illustrates the frequency shift as a function of perturbation. We captured the node voltage in time-domain of the readout circuit and analyzed the spectrum by the fast Fourier transform (FFT). Obviously, due to the elimination of the imaginary part of oscillation frequency, the perturbations do not induce a broadening of the frequency spectrum, as shown in Fig. 3a. At the initial PT-symmetric state, the resonators chose the lower frequency to achieve a steady-state oscillation. Once we changed the ambient temperature, the sensitive capacitance in the sensor introduced a small perturbation into the loss resonator, leading to a shift from the lower branch to the higher branch λ^' . The normalized frequency λ^'  as a function of the perturbation δ is given in Fig. 3b. The experimental results are in good agreement with our theoretical predictions. For sufficiently small perturbations, the response exhibits a slope of 1/3 through logarithmic coordinates, as shown in the inset of Fig. 3b, confirming that the perturbations lead to the cube-root singularity, though the PT-symmetric LC configurations of the linear loss and saturable gain has the second-order of EP degeneracy. 

Fig. 3| Experimental results.

Sensor performance analysis.

  To explicit the influence of noise, we measured and analyzed the phase noise spectrum of nonlinear PT symmetric LC passive wireless sensors by using spectrum analyzer. Fig. 4a illustrates the phase noise spectrum of 0~2 kHz frequency offset with 0~2% perturbations applied on the loss capacitance. And the inset shows the power spectrum at  δ=2%, under which the full width at half maximum (FWHM) of resonances is 0.2 kHz .The spectral linewidth due to phase noise is much lower than the frequency shift (Δƒ=0.54 MHz), enhancing the resolution of temperature sensors. 

  To quantitatively evaluate the overall performance of the sensors, the figure of merit (FOM) in optical sensing is utilized here, which is also referred as the signal-to-noise ratio. It is defined as

FOM=20log₁₀[(Δƒ/Δδ)/FWHM],

where Δƒ/Δδ is actually the sensitivity of the sensor. The FWHM of resonances can be obtained from the phase noise spectrum in Fig. 4a. It remains almost unchanged under asymmetric perturbations up to 2%. 

As illustrated in Fig. 4b, the FOM decrease slightly since the sensitivity of the sensor decreases as the perturbation increases. However, it is higher than 88 dB over the perturbations up to 2%.

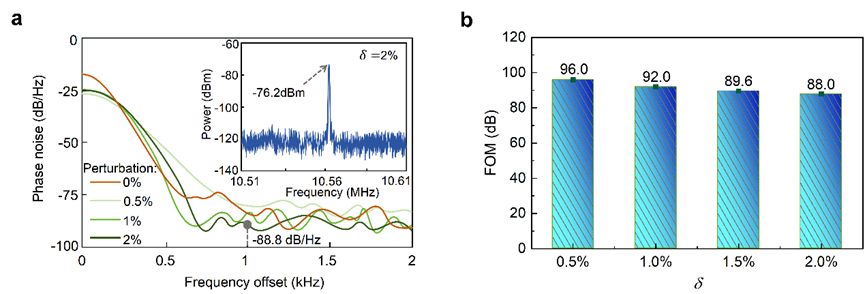
Fig. 4 | The measured phase noise spectrum with 0~2kHz frequency offset (the resolution bandwidth RBW=200 Hz and video bandwidth VBW=20 Hz).

In summary, we have demonstrated that LC passive wireless sensors have an exceptional precision using PT-symmetric LC configurations of the linear loss and saturable gain. The nonlinear gain causes a cube-root frequency detuning from the EP induced by a small capacitance variation on the loss resonator. It also eliminates the imaginary part of the eigenfrequencies and significantly suppresses the noise. Our results resolve a debate on the effectiveness of the exceptional point sensing scheme for inductor–capacitor sensors and enable exceptional precision enhancement for these types of sensors.