Quantum control of mesoscopic spin qubit volumes using nanomagnets
Published in Physics
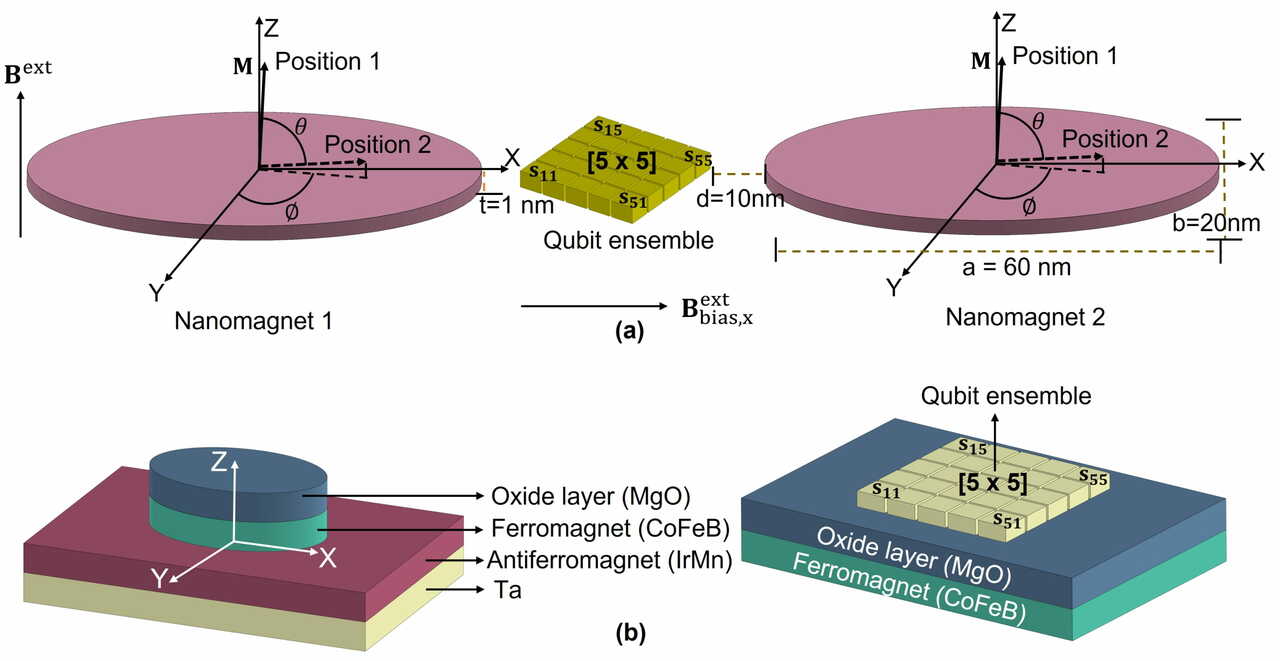
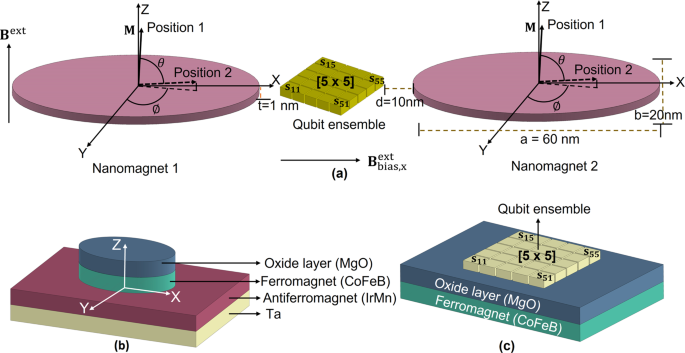
Quantum control of individual qubits densely packed on a chip without cross-talk is challenging due to the difficulty in creating, localizing and confining a strong classical divergence-free field to a small volume of space. It could, however, be an essential component for the implementation of scalable high-fidelity universal quantum gates and quantum algorithms [1]. We show that nanomagnets can be used to create a highly localized magnetic field to selectively to address spin qubits at the nanoscale that are proximal to such nanomagnets without affecting neighboring spin qubits. Furthermore, such nanomagnets can be individually addressed using a crossbar array architecture with top and bottom contacts. Fabrication of such devices is compatible with existing foundry manufacturing processes.
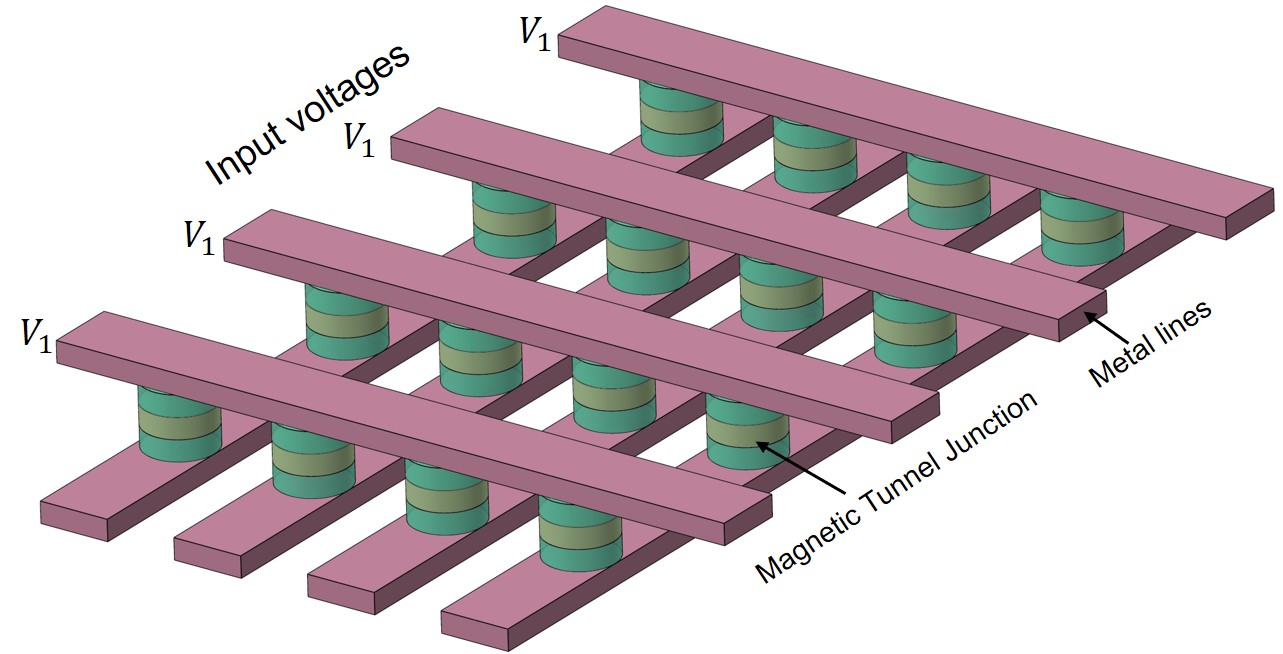
MTJ crossbar array. A crossbar architecture for highly scalable nanomagnets array realized via magnetic tunnel junctions (MTJs).
Current physical implementations of quantum processors utilize qubits based on trapped ions, neutral atoms, nuclear spins, topological qubits, superconducting circuits, quantum dots, semiconductor spin qubits, or NV centers in diamond (or more generally, paramagnetic defects in solids), etc. Nuclear spin qubits were used in the first experimental realization of a quantum algorithm due to their long coherence times and relatively mature pulsed control methods available in NMR experiments [2]. The current prevailing strategy is to combine robust implementations of quantum gates together with suitable quantum error correction codes in order to achieve fault-tolerant quantum computing [3]. Provided that the technology meets a number of requirements known as the DiVincenzo’s criteria, universal quantum computing can be achieved with a small number (set) of quantum gates that allow for the implementation of arbitrary quantum algorithms.

In this work, we show how individual control of spin qubits can be realized using nanomagnets. We propose a technique for addressing spin qubits using voltage-control of nanoscale magnetism, exemplified by the use of voltage control of magnetic anisotropy (VCMA) [4]. We show the feasibility of scalable, small footprint, high-fidelity, and energy-efficient single-qubit quantum gates by tuning the frequency and phase of the nanomagnet’s electric field drive to the Larmor frequency of the spins confined to a nanoscale volume. The nanomagnets magnetization is rotated through the perpendicular magnetic anisotropy variation by applying VCMA. The magnetization dynamics lead to a time-varying induced magnetic field in the qubit volume. The nanomagnets and the qubit volume are assumed to be placed in a uniform external magnetic field pointing along z-axis. The inhomogeneity of the induced field in the qubit volume is reduced by using two identical nanomagnets. Evaluating the spin dynamics evolution, the effective rotation happens at and in 500 MHz and 2 GHz drives, respectively. The rotation happens at and in 500 MHz and 2 GHz frequencies, respectively. We can also implement high fidelity (fidelity: ) and (fidelity: ) gates, and pulses of higher fidelity and robustness can be generated (fidelity of : ) using composite (e.g., Knill) pulses that compensate for errors in the rotation angles or frequency detuning.
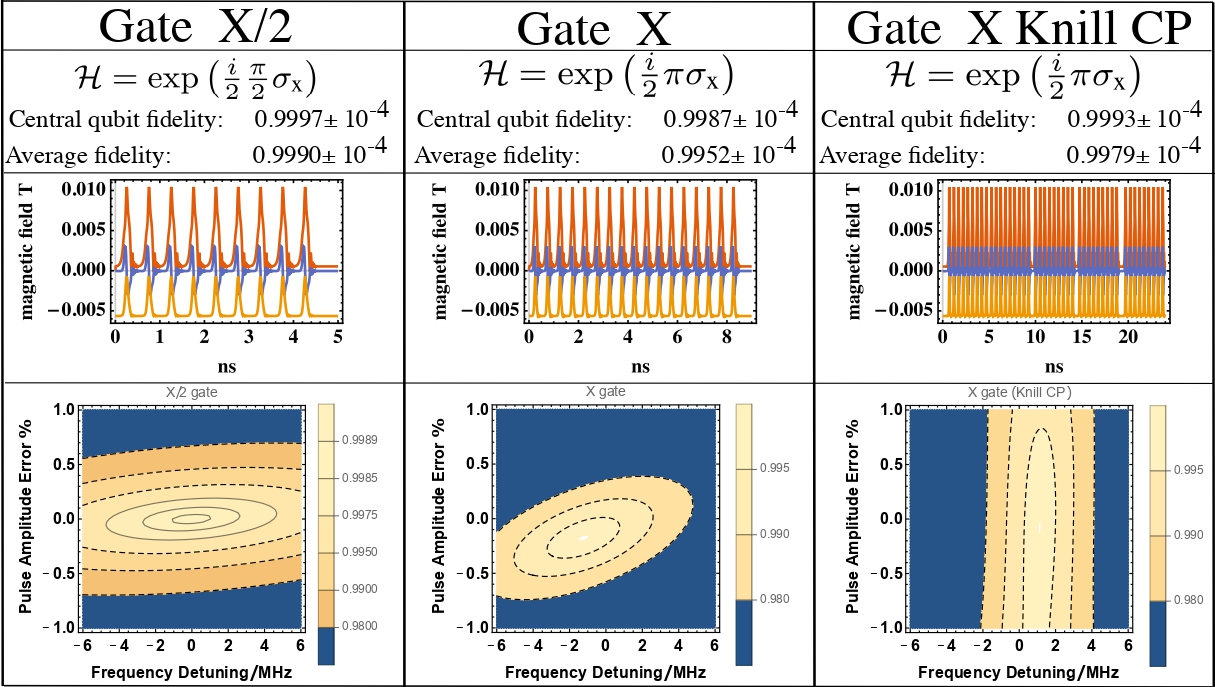
The use of nanoscale magnets allows the production of highly localized and energy-efficient AC magnetic fields to implement single qubit gates. Despite the highly nonlinear response of the magnetization of nanoscale magnets to an electric field, we can achieve high single qubit gate fidelity through the appropriate use of robust composite pulses. Such single-qubit gate operations require only tens of femto-Joules per gate operation and have lossless, purely magnetic field control. The combination of recent developments in spintronics (e.g. energy efficient voltage control of magnetism) together with emerging mesoscale spin qubits that are inherently robust, will stimulate further breakthroughs in energy efficient, robust quantum devices operating at temperatures of a few K [5].
For more information read our article: https://doi.org/10.1038/s42005-022-01041-8
References:
- Preskill, J. Fault-tolerant quantum computation. In Introduction to quantum computation and information, 213–269 (World Scientific, 1998).
- Chuang, I.L., Vandersypen, L.M., Zhou, X., Leung, D.W. and Lloyd, S., 1998. Experimental realization of a quantum algorithm. Nature, 393(6681), pp.143-146.
- Gottesman, D. Theory of fault-tolerant quantum computation. Phys. Rev. A 57, 127–137 (1998).
- Maruyama, T. et al. Large voltage-induced magnetic anisotropy change in a few atomic layers of iron. Nature nanotechnology 4, 158–161 (2009).
- Yang, C. H. et al. Operation of a silicon quantum processor unit cell above one kelvin. Nature 580, 350–354 (2020).
Follow the Topic
-
Communications Physics

An open access journal from Nature Portfolio publishing high-quality research, reviews and commentary in all areas of the physical sciences.
Related Collections
With Collections, you can get published faster and increase your visibility.
Higher-order interaction networks 2024
Publishing Model: Open Access
Deadline: Feb 28, 2026
Non-Markovian quantum dynamics in physical systems: description and control
Publishing Model: Open Access
Deadline: Dec 31, 2025


Please sign in or register for FREE
If you are a registered user on Research Communities by Springer Nature, please sign in