The introduction of quantum annealers (QAs) marks a paradigm shift in scientists' approach to experimenting and simulating quantum systems, offering advantages over traditional experimental methods and numerical approaches. This aligns with Feynman's vision of exploring quantum mechanics through experimentation with individual entities obeying to quantum mechanical principles, a concept made achievable thanks to our unparalleled precision in controlling and observing individual qubits. D-Wave Quantum's quantum annealers have demonstrated their value as a tool for replicating physical phenomena, particularly the frustrated magnetism observed in materials.

In our work, we intentionally set aside the quest of "quantum advantage", wherein quantum computers outperform classical ones, to focus on exploiting a dense network of interconnected qubits to observe the behavior of magnetic moments brought into a quantum superposition. Specifically, we designed an asymmetric hexagonal lattice by connecting  ~2000  qubits to experiment with entropy, fluctuations, and disorder, consistently achieving accurate and reproducible results. Each arrow in the Figure represents a logical qubit hosting a magnetic moment oriented either upwards or downwards. Green dots represent "floppy" qubits with an undetermined orientation for the qubit magnetic moment. 

The system behavior is guided by a Hamiltonian that has two components. The first component describes how the system veers away from having all the magnetic moments in an up-down orientation due to the action of a transverse magnetic field that aligns them all in the same direction. The second part encodes the classical constraints,  enforcing an antiferromagnetic rule favoring antialigned arrows, ultimately determining the qubits' final configuration in the ground state. The device is named in recognition of the action it takes to anneal a quantum state adiabatically: the system starts in a quantum state that represents a superposition of all possible solutions, and evolves over time gradually reducing quantum fluctuations. This process leads the system to settle into a state corresponding to the optimal up-down-moments solution for the given problem.

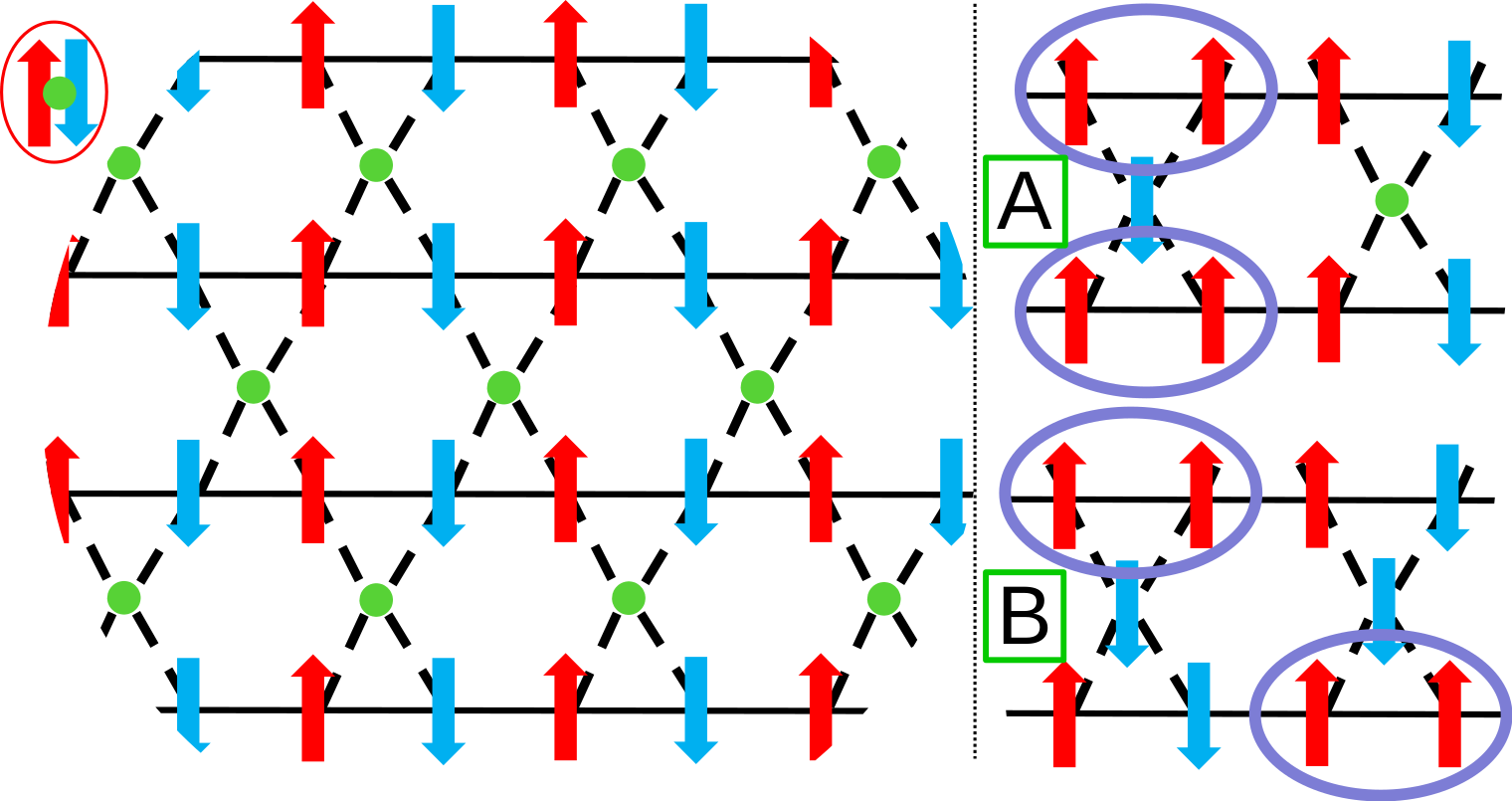
The Figure illustrates two types of antiferromagnetic couplings among the qubits, according to their strength. The solid lines represent a strong along-the-chain qubit-qubit connection. The dashed lines signify a weaker interaction between the qubits in the chain and the intermediate qubits, which prevents parallel chains from being isolated, resulting in an indirect correlation between them.  In the ideal scenario of exactly zero temperature, T=0,  qubits along the chain would exhibit an alternating orientation of their magnetic moments. Because of the total absence of thermal fluctuations and the intermediate qubits are more loosely connected to the chains, there is not a specific orientation that minimizes the overall energy of the system. Intermediate qubits are thus described as "floppy" because, energetically speaking, both up and down orientations are equally probable. Magnetic frustration arises since, regardless of whether they are oriented up or down, there is always some antiferromagnetic qubit-qubit interactions unsatisfied.

The system becomes more interesting as thermal interactions are allowed to kick in. If the magnetic moments are sufficiently energetic to overcome the antialignment rule, two contiguous qubits along the chain may adopt the same orientation. Frustration moves now to the qubits along the chain creating a higher-energy state, while the intermediate qubit is constrained to assume an orientation opposite to that of the other two. The possible presence of a similar defect in a second chain raises a question: if two defects exist in two parallel chains connected by intermediate qubits, what configuration minimizes the total energy of the system? Is it a configuration, A, where two defects align on top of each other, thereby locking one intermediate qubit? Or, is it a configuration, B, where the two defects are positioned at different locations along the chains, thereby locking two intermediate qubits?

The answer requires some analysis of the system's entropy. Conventional wisdom says that entropy is a quantifiable measure of the degree of randomness and disorder within a system, especially when subjected to fluctuations. According to the Boltzmann's expression, S ∼ ln Ω  the higher the number of states Ω accessible to the system, the higher the entropy S. And the higher the entropy, the lower the Helmholtz free energy, F=U-TS, which depends on the product of its absolute temperature with entropy. For two systems with the same internal energy U, the one with the highest entropy will be more energetically favorable.

This brings us back to the context of floppy qubits. Tallying up the energy from pairwise interactions, both configurations A and B have the same internal energy U. At very low T, barely some defects would be formed. At high T, the system would be paramagnetic and highly disorganize.  Intuitively, one might assume that configuration B, with a more scattered distribution of defects (higher disorder), would have higher entropy and, consequently, lower free energy. However, contrary to expectations, the most likely configuration is of type A. The explanation lies in the presence of a floppy magnetic moment that increases 
entropy by ln 2, where 2 accounts for the two additional up and down states absent in configuration B. Therefore, among configurations with the same number of paired-aligned qubits, those grouped around a single pinned qubit, releasing another, exhibit lower free energy and are more likely to be found by the quantum annealer as a lower energy state.

The role of the QA is to sample the ground state manifold of the system and estimate the amount of A and B type configurations. The result was that, at a narrow effective temperature range, in between low-defect (low T) and paramagnetic (high T) configurations the QA is very effective at retrieving configurations with a rich amount of clustered defects. Within a controlled environment free of spurious interactions, and in which variables such as pressure, volume, or chemical potentials play no role, allowing the effects of entropy to be observed with a high degree of accuracy, the QA has the ability to explore the low-energy manifold of the system.

If we described  an scenario where a certain amount of thermal fluctuations gave rise to long-range ordering, quantum fluctuations were observed to further enhance that. But that will have to await a future blog post.