Remote Focused Encoding and Decoding of Electric Fields through Acoustoelectric Heterodyning
Published in Physics

Solid-state electromagnetic heterodyning has been central to computing and telecommunications. Heterodyning enables frequency shifting to optimise signal transmission over long distances, though has thus far lacked remote targeting ability. A method capable of remote, focal heterodyning in liquid materials would enable concepts such as liquid computation and telecommunications to be developed.
A long-standing goal in biomedicine has been to non-invasively and focally modulate and record electrophysiological signals at depth. To these ends, it would be advantageous to harness the focusing ability of acoustics due to their smaller wavelengths compared to electric fields, whilst still interacting with the body in terms of well understood electrical interactions. This combination of advantages led us to investigate the acoustoelectric effect, initially detected by Herzfeld and Rock [1] who noted that the conductivity of saline solution was modulated via acoustic waves. The application of an ultrasonic field to an electrolyte changes the ion density and mobility periodically thereby changing the conductivity at the ultrasound frequency [2]. They noticed that this conductivity modulation, when a constant current is present, elicits and potential change. Recently, several studies have used this theoretical foundation and the lead-field reciprocal principle to estimate the current density distribution in tissues using ultrasound and surface electric potential recording aka ultrasound current source density imaging [3, 4].
Our recent article in Nature Communications Physics, predicts acoustoelectric heterodyning via mathematical and computational field modelling, accounting for the vector nature of the electrolytic acoustoelectric interaction. We then experimentally validate this by applying a focal acoustic field to an electric field in electrolytes, demonstrating that we can mechanically heterodyne the electric field at just the focal area of the ultrasound, inducing new electric field components that oscillate at the sum and difference frequencies of the applied fields.
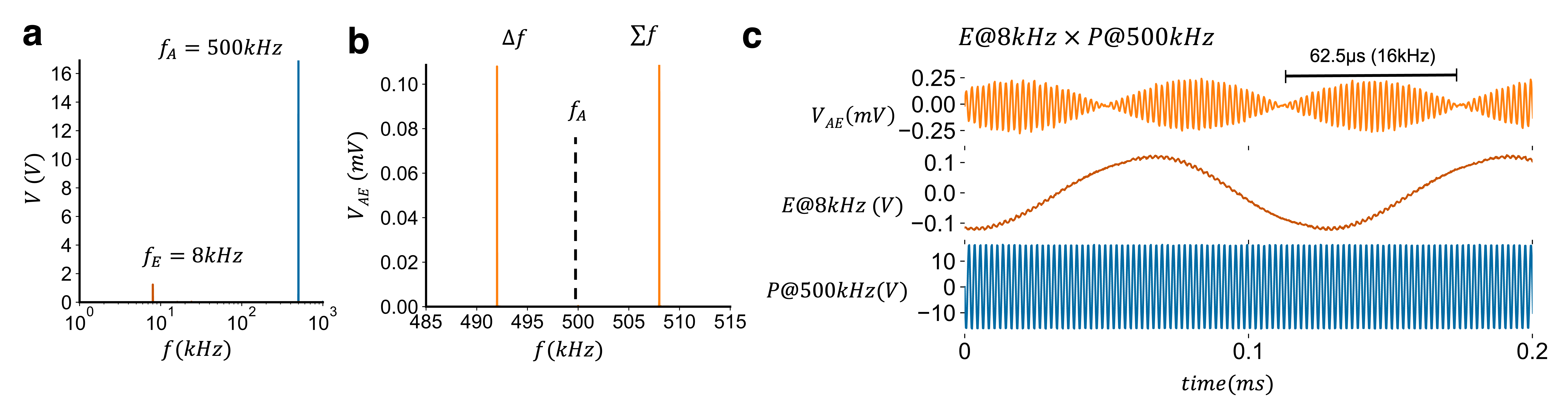
Fig 1. (a) Frequency spectrum of the experimentally applied acoustic and electric field frequencies. (b) Measurement at the acoustic focus of the potential around the acoustic frequency clearly shows the difference and sum frequency. (c) Time-series trace of the resulting measured electric field alongside the applied electric (E) and acoustic fields (P).
The heterodyned electric field has a unique shape dependent on the relative applied fields' orientation as predicted by simulation and proven through experimental measurement. We found that when the electric field was applied in parallel with the direction of the acoustic field propagation, the generated electric field had a three-dimensional topology with a concentric ring dipole in the radial direction and a periodic linear multipole in the axial direction (relative to the acoustic field propagation) with the ultrasound wavelength. When the electric field was applied perpendicular to the direction of acoustic field propagation it changed the topology and strength of the generated electric field. Specifically, the concentric ring geometry in the radial direction changed to a dipole. Furthermore, the amplitude of the generated electric field was four times larger when the acoustic and electric fields were aligned, compared to when they were perpendicular.
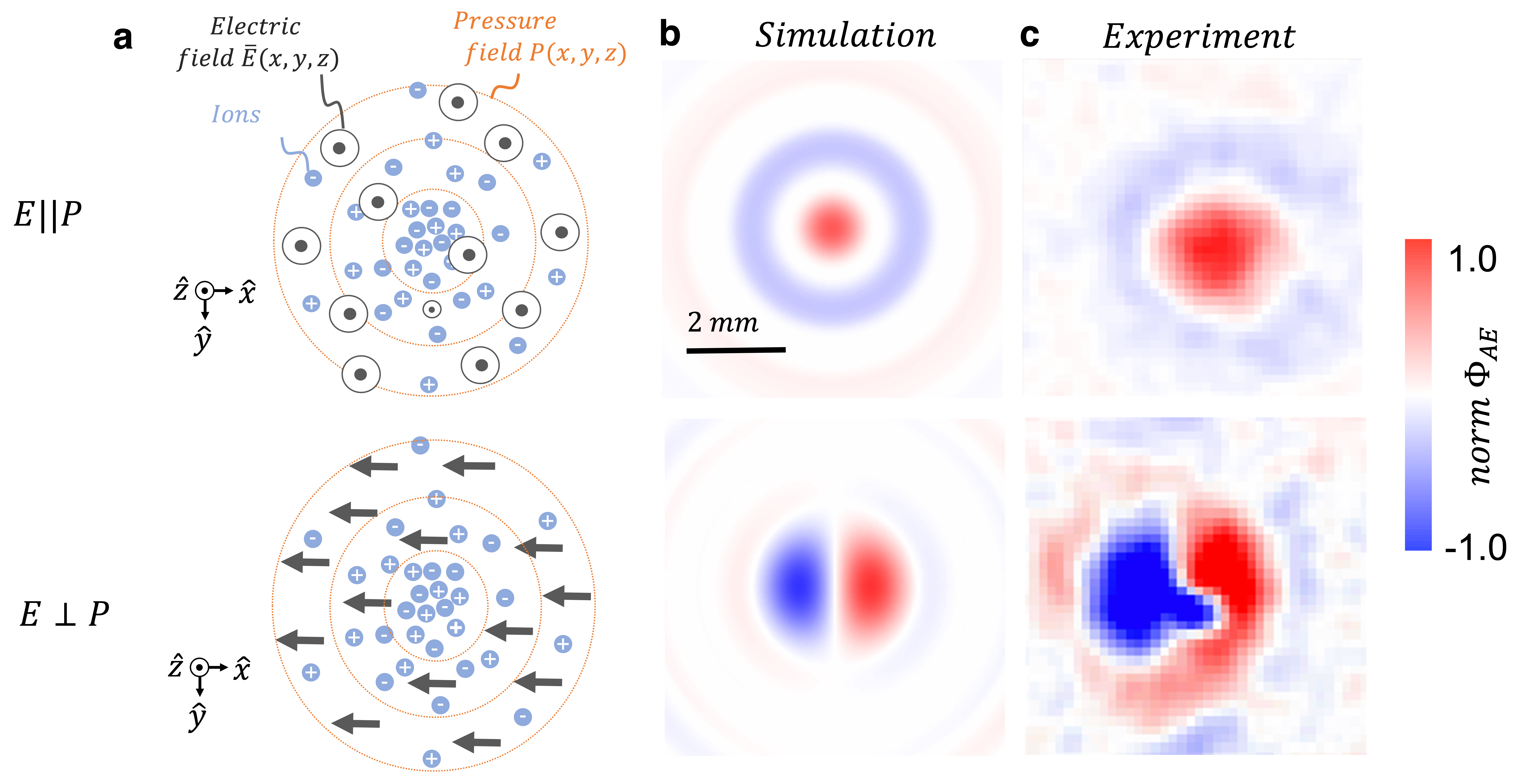
Fig 2. (a) Positioning of applied acoustic and electric fields in parallel and perpendicular to each other, at the focal point of an ultrasound transducer in ionic solution (b) Simulated spatial topology prediction in the same plane, at both field alignments (c) Experimental verification in physiological saline of the spatial topology and orientation dependence of the generated electric field on the applied fields.
These fundamental qualities of the acoustoelectric effect, enable us to encode and decode electric fields at depth with improved amplitudes and topological accuracy. To encode a signal at a focal location we apply an electric field at a small difference frequency from the acoustic frequency, to produce a low frequency field based on the difference between the two applied fields at the remote focal area of the acoustic source. To decode an electric signal that is generated at depth, a complex ionic current signal in the target location is focally mixed with a sinusoidal acoustic signal via the acoustoelectric effect to generate a detectable electric signal with the original information modulated up to the acoustic frequency (see Fig 3.). The electric potential of the modulated signal is recorded and computationally demodulated to recover the original signal via in-phase and quadrature (IQ) demodulation. In IQ demodulation, the signal is multiplied by two sinusoidal waveforms at the known frequency and a phase difference. The resultant signals are low pass filtered (LPF) to yield the signal and the phase shifted signal from which the instantaneous amplitude and phase of the original signal are recovered.
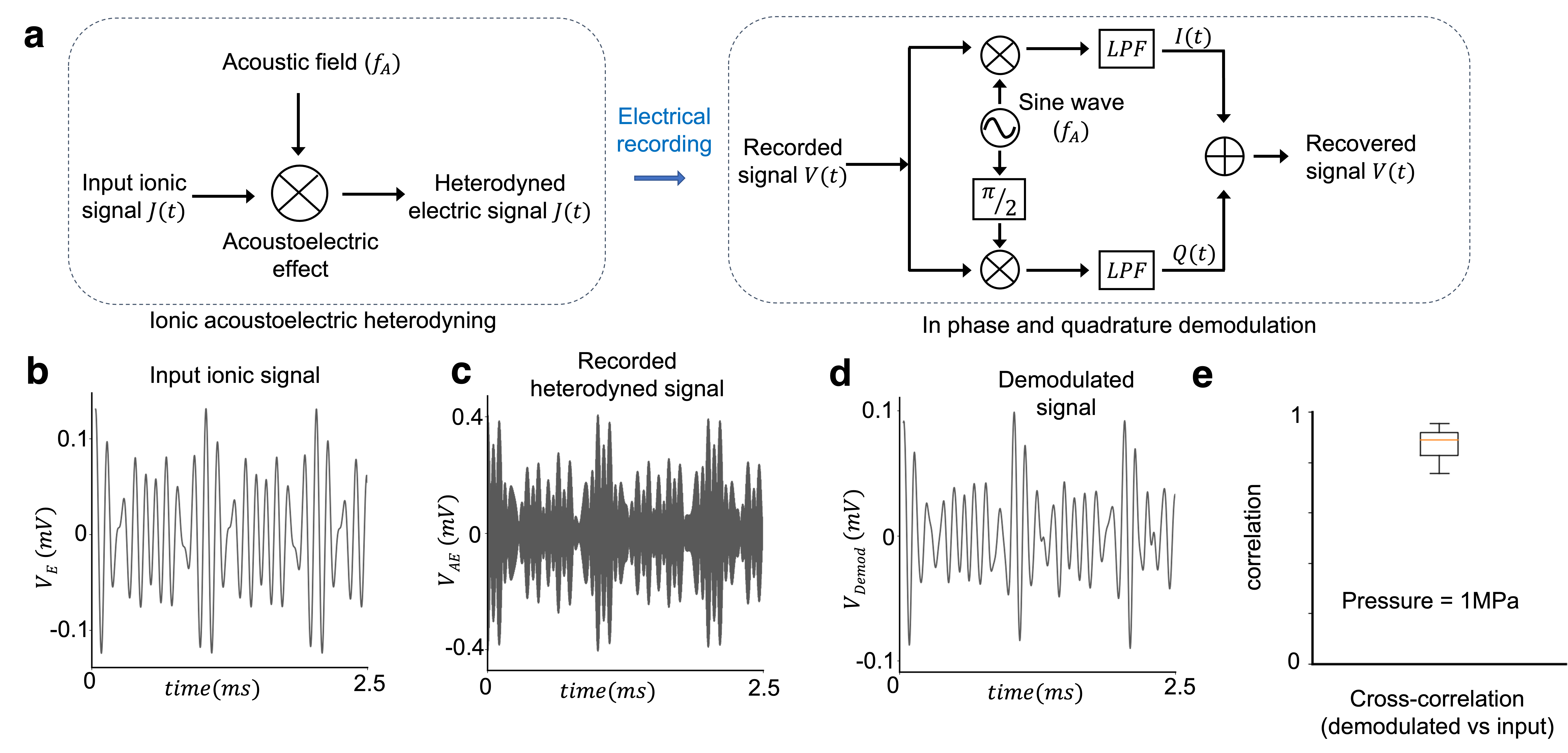
Fig 3. (a) Schematic of the acoustoelectric heterodyning and demodulation pathway. (b) Input complex electric signal occurring at the focal point of the ultrasound (c) recorded potential of the acoustically heterodyned electric signal, high pass filtered in software to remove the applied ionic signal. (d) computationally demodulated signal. (e) Cross-correlation between the demodulated signal and the original input signal.
Given the broad use of electrostatic focusing lenses [5], the potential translational prospects for acoustically controlled electric field lenses are exciting. Acoustoelectric heterodyning could enable non-invasive focal modulation and recording of electrophysiological signals at depth and future studies in animal models will be able to test the feasibility of such an approach. These unique properties of the electromechanical interaction open translational avenues in electrochemistry, bioelectronics, and medicine.
For more information read our article, and don't forget to also see the supplementary material which gives a more in depth mathematical proof, artefact study and more.
References
[1] F. E. Fox, K. F. Herzfeld, and G. D. Rock, The effect of ultrasonic waves on the conductivity of salt solutions, Phys. Rev., vol. 70, no. 5–6, pp. 329–339, 1946.
[2] Lavandier, B., Jossinet, J. & Cathignol, D. Experimental measurement of the acousto-electric interaction signal in saline solution. Ultrasonics 38, 929–936, 2000.
[3] Ragnar Olafsson, Russell S. Witte, Sheng-Wen Huang, M. O. Ultrasound Current Source Density Imaging. IEEE Trans Biomed Eng, 55, 1840–1848, 2008.
[4] Yang, R., Li, X., Song, A., He, B. & Yan, R. A 3-D reconstruction solution to current density imaging based on acoustoelectric effect by deconvolution: A simulation study. IEEE Trans Biomed Eng 60, 1181–1190, 2013.
[5] Blewett, J. P. Radial Focusing in the Linear Accelerator. Physical Review 88, 1197–1199, 1952.
Follow the Topic
-
Communications Physics

An open access journal from Nature Portfolio publishing high-quality research, reviews and commentary in all areas of the physical sciences.
Related Collections
With Collections, you can get published faster and increase your visibility.
Higher-order interaction networks 2024
Publishing Model: Open Access
Deadline: Feb 28, 2026
Physics-Informed Machine Learning
Publishing Model: Hybrid
Deadline: May 31, 2026



Please sign in or register for FREE
If you are a registered user on Research Communities by Springer Nature, please sign in