The Neural Coding Framework for Learning Generative Models
Published in Electrical & Electronic Engineering
Backpropagation of errors has been a foundational algorithm to the field of machine learning, playing a key role in the design of artificial neural networks (ANNs) that can categorize, forecast, play games, and learn generative models of data. However, a long-standing criticism of backpropagation (backprop) has been its biological implausibility -- it is unlikely that the billions of neurons that compose the human brain adjust the strengths of the synapses that connect them through the same mechanisms that underpin backprop.
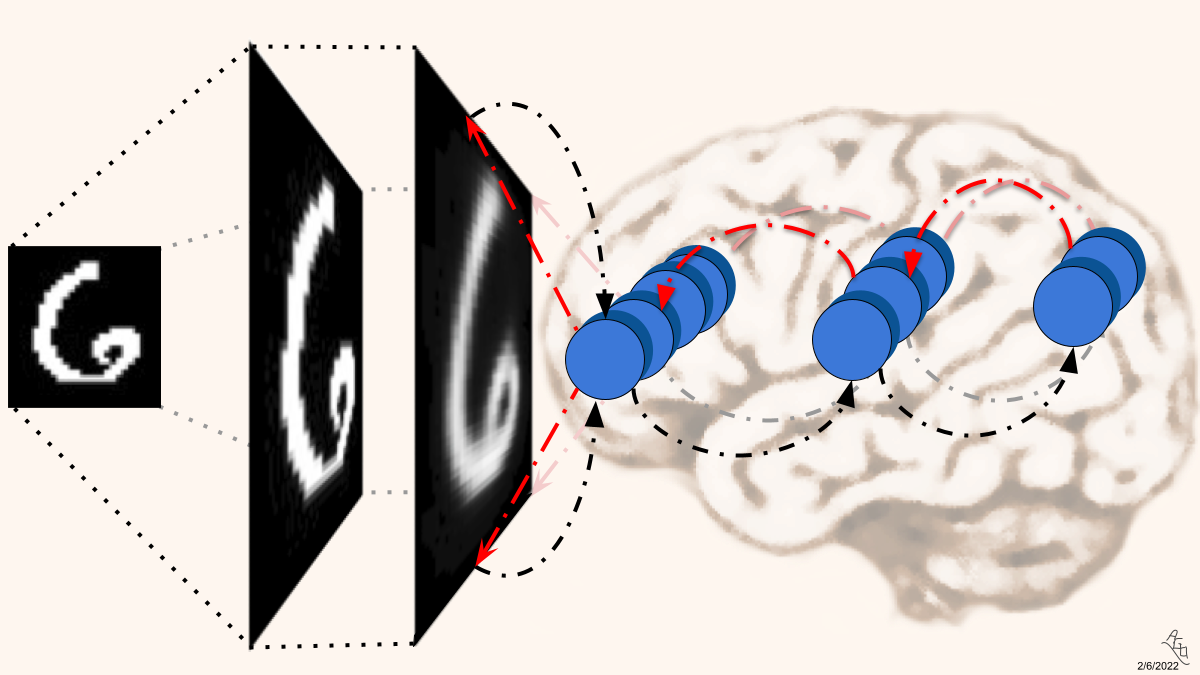
a number. Notice that an NGC circuit embodies the notion that neurons in the brain operate under a "guess-
then-correct" process -- neurons first make predictions of a sensory input (such as the image of the number
six, depicted above) and then correct their internal model of their environment based on the actual observed
data. These neurons, arranged in a hierarchy (or partial hierarchy), continually do this throughout a lifetime,
progressively building up a flexible and adaptable model of the world within the synapses that connect them.
Backprop, when used to adjust the weights of a modern-day ANN, requires that the synapses that connect the neurons within the ANN form a direct pathway for carrying forward information from an input layer (where sensory data is placed) all the way to an output layer (where a prediction about the sensory data is made). Then, after information has passed through the network in this fashion, error signals related to how far off the ANN's predictions were with respect to the real data must be carried back along that very same pathway, in reverse. As the error travels back across this path (also referred to as the global feedback pathway), neurons along the way must also be able to communicate information about the derivative of their own activation function and, ultimately, must wait for the neurons ahead of them to transmit their particular error signals backwards before they know how to manipulate their own synapses (also known as the update-locking problem). Furthermore, backprop produces teaching signals that only affect the ANN's synaptic strengths, meaning that these signals do not affect the neural activities directly.
In contrast to those in backprop-based DNNs, neurons in the brain largely make adjustments to their synapses locally, meaning that they use the information immediately available to them after firing. In essence, neurons do not wait on those in distant regions to communicate back to them in order to adjust their synaptic efficacies. It has been observed, for example, that neocortical regions learn/extract spatial patterns for small parts of the visual space and only after the information has been processed through several layers of a hierarchy do these spatial patterns combine to represent much of the visual space globally (resulting in representations that correspond to complex shapes and objects). The circuits themselves adhere to local, recurrent connectivity patterns, with constituent neural units also laterally interacting with one another in the effort to encode internal representations of sensory data.
Predictive processing theory fits well with the above picture, positing that the brain operates like a hierarchical model whose levels are implemented by (clusters of) neurons. If these levels are likened to regions of the brain, the neurons at one level or region attempt to predict the state of neurons at another level or region, locally adjusting their internal activity values as well as their synaptic efficacies based on how different their predictions were from observed signals. Furthermore, these neurons utilize various mechanisms to laterally stimulate and suppress each other to facilitate contextual processing, such as grouping and segmenting visual components of objects within a scene.
Motivated and inspired by the theory of predictive processing, we developed the neural generative coding (NGC) computational framework and focused on the challenge of unsupervised learning, where an intelligent system must learn without the use of explicit supervisory signals, e.g., human-crafted labels. Specifically, we examined how NGC can be utilized to learn generative models, or probabilistic systems that are capable of synthesizing instances of data. Once such systems are trained, we may inject them with noise to output patterns that resemble those of databases of collected samples. Our framework emulates many key aspects of the neurobiological predictive processing narrative, notably incorporating mechanisms for local learning, layer-wise predictions, learnable recurrent error pathways, derivative-free stateful computation, and laterally-driven sparsity (where internal neurons compete for the right to activate).
The functionality and generalization capability of our framework was demonstrated by deriving and implementing several concrete models, including variants of which were shown to recover classical models of predictive coding. Experimentally, across four different benchmark datasets, the family of models was shown to be competitive with powerful, backprop-driven ANNs with respect to auto-associative memory recall and marginal log likelihood1 while requiring far fewer neurons to fire, i.e., the activities of the NGC models were found to be quite sparse. Notably, we found that the NGC models outperformed the ANNs on two tasks that they were not originally trained on, i.e., image classification and auto-associative pattern completion. As a result, this study presents promising evidence that unsupervised, brain-inspired neural systems are performant while resolving many of the key backprop-centric issues.

For the machine learning, computational neuroscience, and cognitive science communities, we believe that the NGC framework offers an important means of demonstrating how a neural system can learn something as complex as a generative model using mechanisms and rules that are brain-inspired. This, we furthermore believe, offers a pathway for shedding the constraints imposed by backprop in the effort to build general-purpose learning agents that are capable of emulating more complex human cognitive function.
In order facilitate and drive further advances and discoveries in predictive processing research through the NGC framework, we have developed a general software library, which we named NGC-Learn, to aid researchers in crafting and simulating their own NGC circuits/models.
1 Marginal log likelihood, in short, measures how good a generative model is at estimating the probability of the real- world data itself.
Follow the Topic
-
Nature Communications

An open access, multidisciplinary journal dedicated to publishing high-quality research in all areas of the biological, health, physical, chemical and Earth sciences.
Related Collections
With Collections, you can get published faster and increase your visibility.
Women's Health
Publishing Model: Hybrid
Deadline: Ongoing
Advances in neurodegenerative diseases
Publishing Model: Hybrid
Deadline: Mar 24, 2026


Please sign in or register for FREE
If you are a registered user on Research Communities by Springer Nature, please sign in