Title: Exponential improvement of machine learning algorithms for quantum problems
Published in Physics and Computational Sciences
Ground States
One problem that physicists care a lot about is finding the ground state of a quantum system. Here, the ground state is the state of the system with the lowest energy (think of a ball lying at the bottom of a bowl). What’s so special about ground states? Learning about the ground state can tell us how its corresponding system will act at low temperatures. But “low temperature” here is relative, and, in fact, from the point of view of electrons, room temperature is considered to be very low. Thus, for electronic systems (e.g., metals, magnets), the ground state describes the state of the system in everyday life fairly well. In this way, understanding the ground state can provide us with insights into different properties of quantum systems. In particular, this knowledge can help us learn about the chemical properties of molecules with the potential for far-reaching applications in chemistry and materials science.
The catch is that finding ground states is quite difficult for classical computers. Despite lots of research for classical algorithms to solve this problem, a fully general solution still remains out of reach. Good algorithms exist for certain special cases, but none have been found for the general case. Quantum computers will be able to solve this problem efficiently, but current devices are not quite up to the task yet, with their limited size and error-prone operations. While quantum computers are still being developed, are there other ways to leverage classical computers to help us find ground states?
Machine Learning for Predicting Ground States
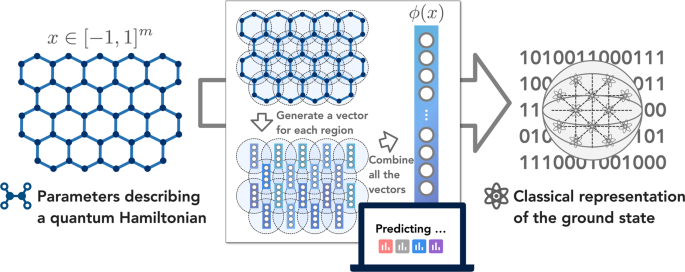
A recent paper [1] in Science proposed the first provably efficient classical machine learning (ML) algorithm for predicting ground state properties after learning from some amount of training data. In contrast, highlighting the difficulties discussed above, they also showed that no efficient classical algorithm that does not learn and adapt from data can achieve the same performance guarantees (under standard complexity theoretic assumptions).
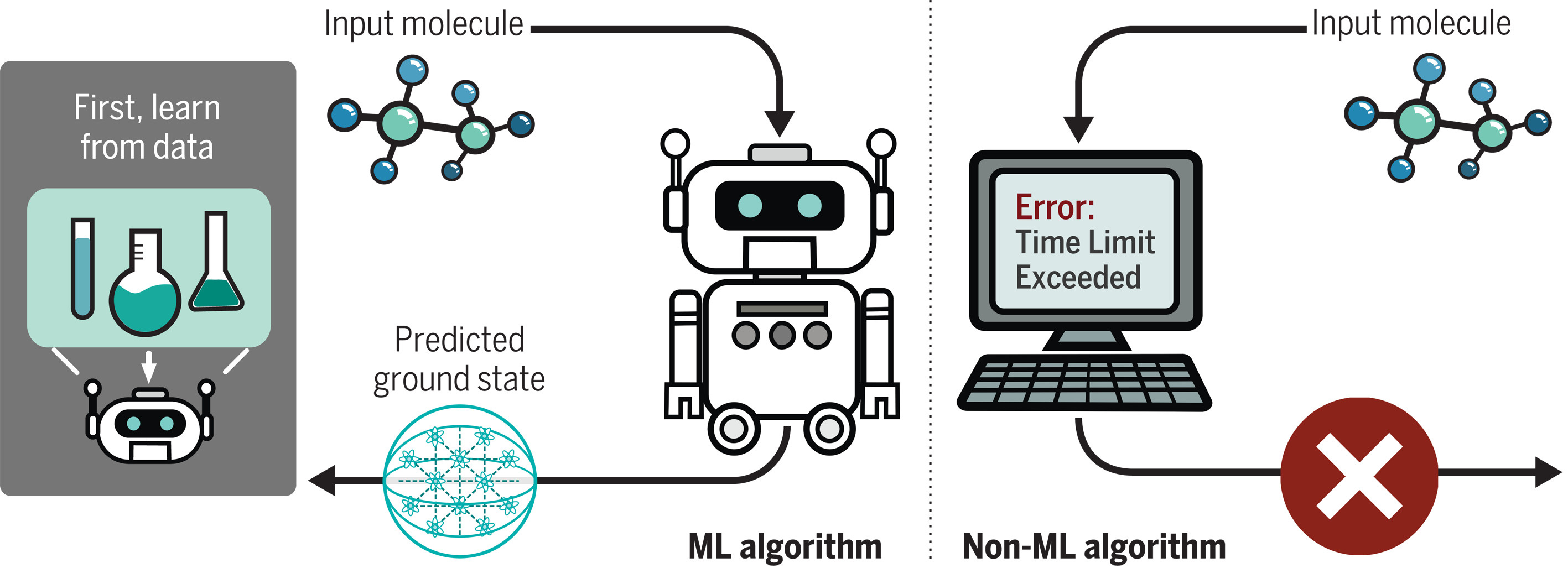
At first glance, this appears to solve the problem completely assuming sufficient training data is available. However, while the algorithm is efficient in theory, requiring polynomially many training data points and a polynomial runtime (in the number of qubits), these polynomials are huge. This means that one would have to perform a large number of physical experiments to obtain such training data, which is practically infeasible.
Exponential Improvement
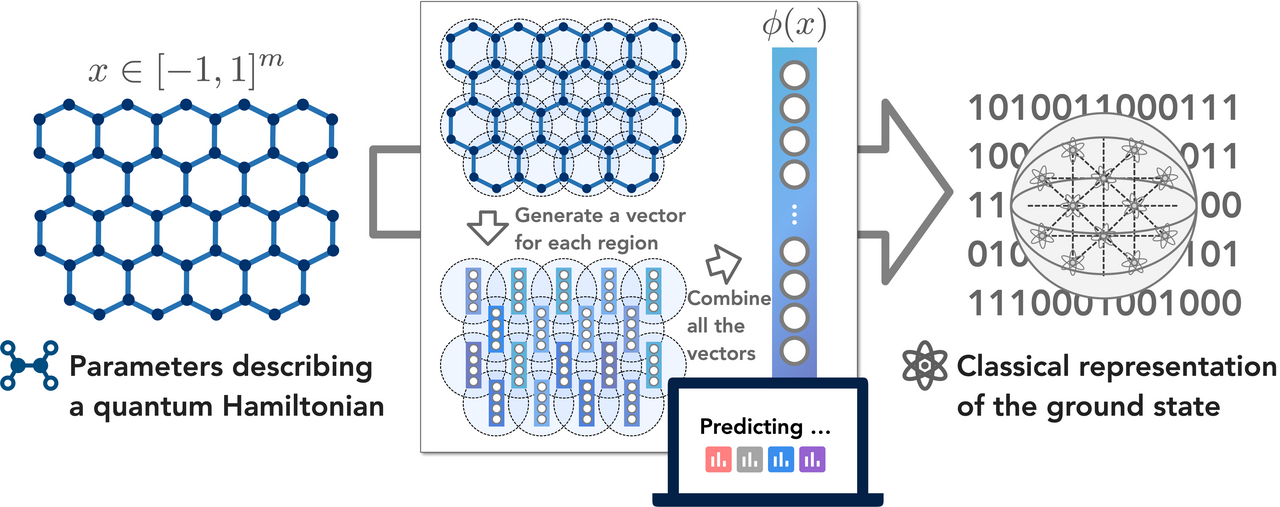
Our work, “Improved machine learning algorithm for predicting ground state properties,” published recently in Nature Communications, fixes this issue by rigorously proving that the amount of training data can be exponentially reduced (with respect to system size). We obtain this drastic improvement by incorporating knowledge of the geometry of the underlying quantum system into the ML algorithm. This allows us to better characterize the ground state and approximate it by a linear function on a high-dimensional feature space. Combining these pieces, we show that the number of training data points need only scale logarithmically in the number of qubits.
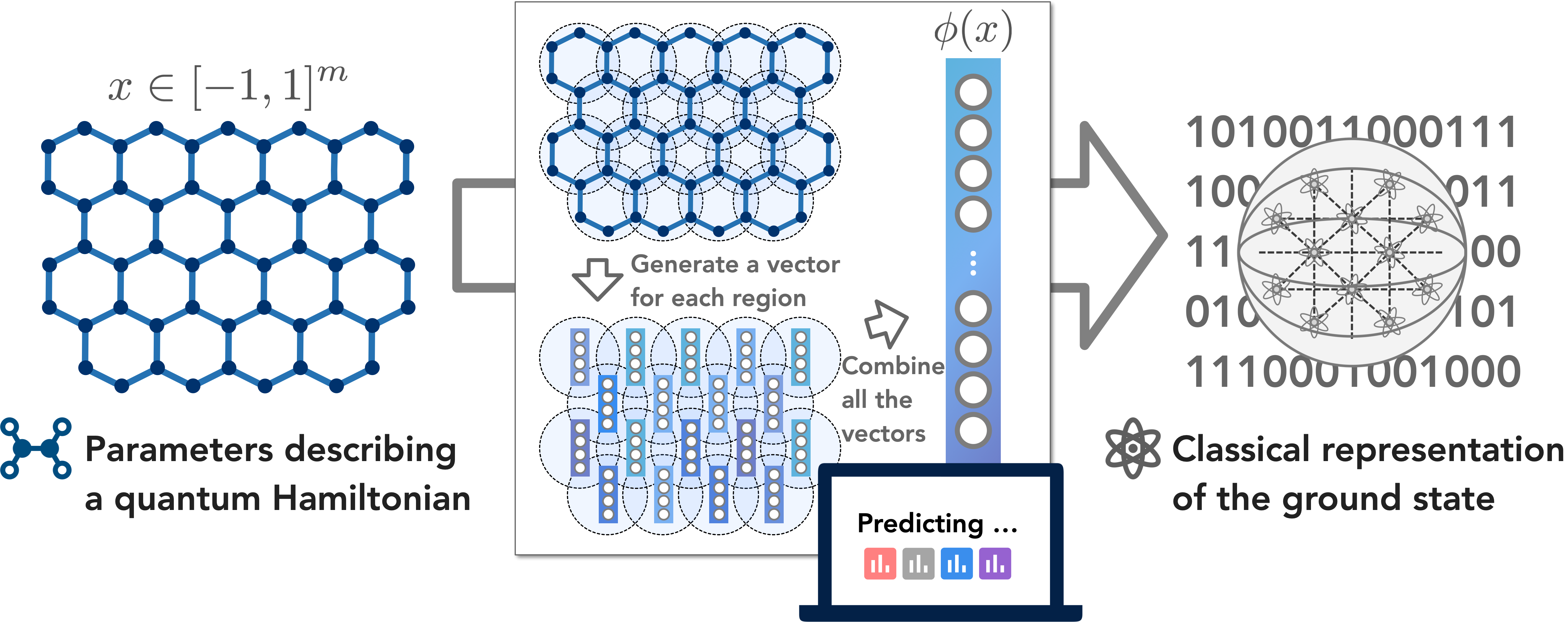
We also perform numerical experiments to assess the performance of our ML algorithm in practice, predicting ground state properties in the 2D antiferromagnetic random Heisenberg model. Our experiments confirm the favorable scaling with respect to the system size. In particular, as the system size increases from 20 qubits to 45 qubits, the prediction error increases very mildly, reflecting the logarithmic scaling.
Outlook
In summary, our work provides a rigorous guarantee on the amount of training data required for learning ground state properties and proves that it can be exponentially reduced from that of previous work. The logarithmic sample complexity established in our work raises the hope of using ML to address practical problems in quantum physics, chemistry, and materials science by learning from the relatively small amount of data we can feasibly gather from real-world experiments. There are still several questions that remain open: Can ML algorithms learn properties of low-energy excited states rather than ground states? Can quantum ML algorithms predict ground states properties using even less training data than any classical ML algorithm?
Acknowledgements
This work was a collaboration between researchers at the Institute for Quantum Information and Matter at the California Institute of Technology (Caltech) and Johannes Kepler University.
References
[1] H.-Y. Huang, R. Kueng, G. Torlai, V. V. Albert, J. Preskill. Provably efficient machine learning for quantum many-body problems. Science 377, eabk3333 (2022).
Follow the Topic
-
Nature Communications

An open access, multidisciplinary journal dedicated to publishing high-quality research in all areas of the biological, health, physical, chemical and Earth sciences.
Ask the Editor – Space Physics, Quantum Physics, Atomic, Molecular and Chemical Physics
Got a question for the editor about Space Physics, Quantum Physics, Atomic, Molecular and Chemical Physics? Ask it here!
Continue reading announcementRelated Collections
With Collections, you can get published faster and increase your visibility.
Women's Health
Publishing Model: Hybrid
Deadline: Ongoing
Advances in neurodegenerative diseases
Publishing Model: Hybrid
Deadline: Dec 24, 2025





Please sign in or register for FREE
If you are a registered user on Research Communities by Springer Nature, please sign in