A new type of quantum tunnelling predicts the lifetime and mechanism for the decay of singlet oxygen
Published in Chemistry

On a cold October morning in 2020, in the thick of the pandemic, I arrived in Zürich, starting as a research assistant on a seemingly simple project: apply the then newly developed theory for quantum tunnelling to the decay of singlet oxygen. Unbeknownst to us, hiding behind the facade of simplicity was a completely new class of quantum tunnelling. What began as a computational chemistry semester project on applying an existing theory to real-world problems, blossomed into a theory development doctoral thesis on a new theory for tunnelling.
Background on singlet oxygen
While oxygen (O2) mostly exists in a relatively unreactive form (a triplet, where the spins of the electrons are aligned), it can be excited to a far more reactive form (a singlet, where the electron spins are in opposing directions). This reactive form is known to wreak havoc on living cells by initiating chain reactions involving radicals, which eventually result in cell death. However, this reactivity can also be exploited to kill pathogens and cancer cells.
As chemists, we seek to understand the factors that influence its reactivity. The reactive singlet eventually decays back to the triplet, via a process that involves a flipping of the spins (spin crossover). The rate at which it decays determines how long the singlet state exists, i.e., its lifetime. The longer the lifetime, the more it can react.
Despite its ubiquity in nature and an abundance of experimental data on its lifetime under various conditions, very little is known about how the decay takes place at a molecular level, i.e., its mechanism. Previous studies have attempted to explain the mechanism assuming it passes through a molecular geometry where the singlet and triplet states have the same energy, the minimum energy crossing point (MECP). In such a framework, the MECP effectively plays the role of a transition state between the singlet and triplet states.
However, this approach does not explicitly consider quantum tunnelling, a phenomenon where particles appear to “tunnel through” the energy barrier that prevents a reaction from taking place spontaneously. Based on our previous studies on other spin-crossover processes, we had reason to believe that tunnelling was the key to finally elucidating the reaction mechanism. In fact, our initial calculations showed that in the absence of tunnelling, a mechanism through the MECP is predicted to result in a lifetime longer than the age of the universe!
The trials and tribulations of tunnelling
Back in 2020, when we started working on this project, the group had just developed a new theory of quantum tunnelling, called golden-rule instanton theory. This theory is based on the path-integral representation of quantum mechanics, an entirely equivalent representation of quantum mechanics extensively developed by Richard Feynman in the 1960s.
With instanton theory, tunnelling can be understood as the molecule undergoing dynamics in imaginary time. Imaginary-time dynamics are not very different from the usual real-time dynamics (Newton’s laws of motion), barring a few sign changes and factors of the imaginary unit i here and there. This simple but powerful idea allows us to use the much simpler classical equations of motion to study an inherently quantum effect.
However despite showing great results on other spin-crossover reactions, golden-rule instanton theory was proving difficult for the spin crossover of singlet oxygen. While we were able to locate a tunnelling path that obeyed Newtonian dynamics, its second derivative had the wrong sign. While this might sound like a minor detail at first, it plays a crucial role in the derivation of instanton theory. The usual suspects were checked first: bugs in the code and/or maths. We double-checked that global translations and rotations, under which the system should be invariant, were being handled correctly. None of this proved to be the cause of the flipped sign. Something was fundamentally different about this problem.
A new type of tunnelling and its implications for spin crossovers and beyond
After a detailed examination of all the steps involved in the derivation, we were able to narrow down the cause of the flipped sign: the existence of a singularity elsewhere in the complex-time plane. The derivation relies on the rules of complex analysis, which allows us to simplify integrals of complex functions by changing the integration contour (Cauchy’s integral theorem). However, these rules break down if the modified integration contour contains a singularity, necessitating a new contour.
The new contour gives rise to a new instanton rate equation and a corresponding tunnelling mechanism, dominated by the singularity. At the singularity, there exists an infinite set of tunnelling paths, each with the same probability. In the context of singlet oxygen (or any chemical reaction where this method is applicable), this implies the existence of an infinite set of reaction mechanisms.
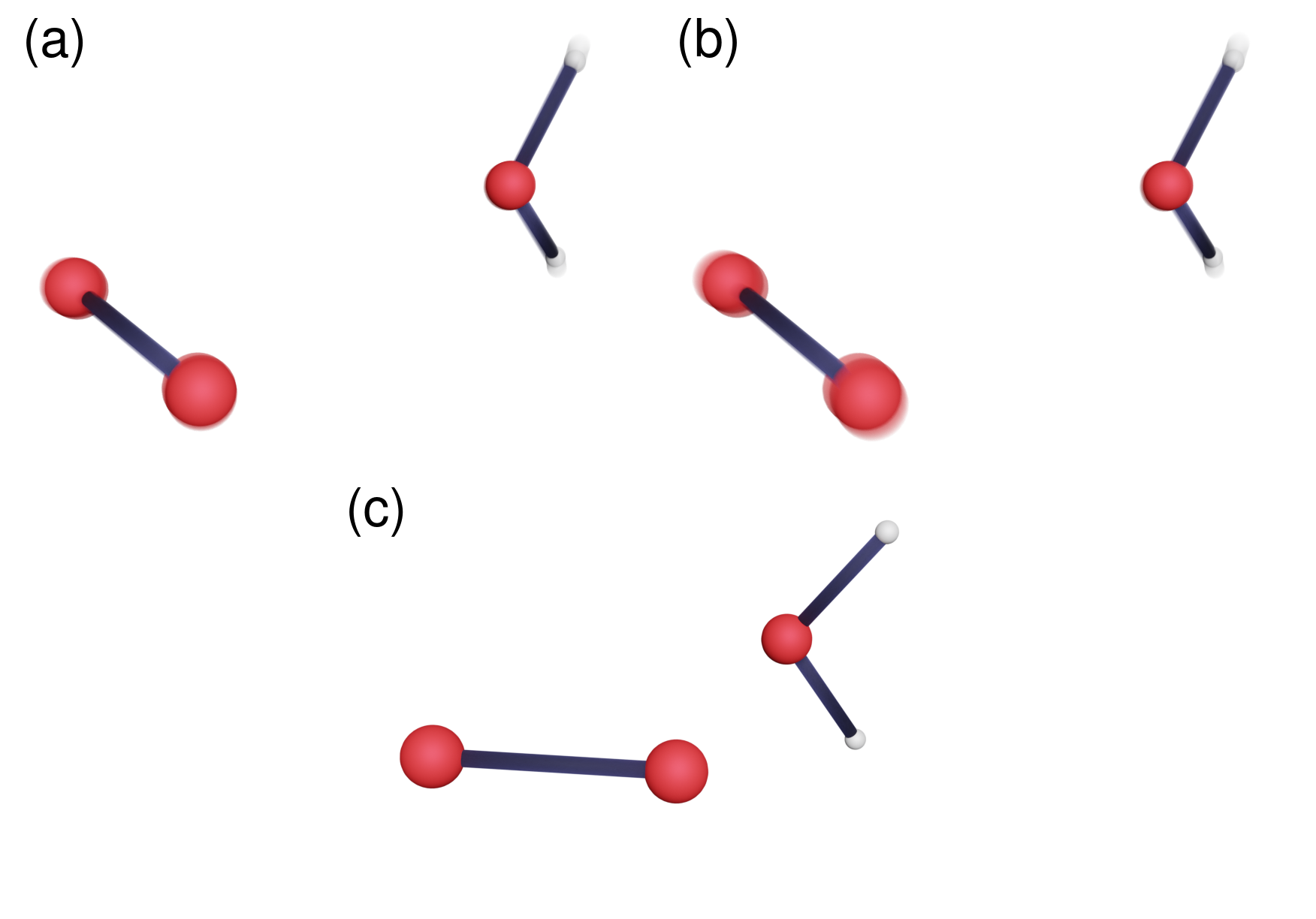
This new mechanism is able to correctly predict experimental data on singlet oxygen lifetimes in water and its rather large change upon replacing the hydrogen atoms in water with deuterium (kinetic isotope effect), across a range of temperatures. Relative to the non-tunnelling mechanism (which predicted a lifetime longer than the age of the universe), it shows an enormous 27 orders of magnitude speedup! This is by far the largest tunnelling-related speedup of a chemical reaction we have ever come across. Unlike the non-tunnelling mechanism, the tunnelling mechanism does not pass through the MECP (a phenomenon known as corner cutting, see Figure 1) and involves the motion of the relatively heavy oxygen atoms. This is unusual as lighter, faster atoms are more “quantum” and are therefore expected to be more involved in tunnelling.
The explanation for these anomalies is quite simple: the singularity is likely to appear in cases where the MECP is very high in energy relative to the thermal energy of the system at a given temperature. When this is true, as far as the system is concerned, the MECP might as well not exist and it thus looks for a ‘short-cut’ corner-cutting mechanism instead. This mechanism can have a special symmetry, where it is possible to modify it such that the resulting change in the tunnelling probability from the singlet state cancels exactly with that from the triplet state. This gives rise to an infinite set of mechanisms which have the same tunnelling probability.
With this new method, we have not only managed to provide a mechanism for the decay of singlet oxygen that is consistent with experimental results, but also uncovered a new type of quantum tunnelling that challenges our understanding of tunnelling and reaction mechanisms. We expect that this method is applicable to a large number of photochemical reactions, including singlet oxygen decay in other solvents, where we expect to find large speedups due to tunnelling.
Follow the Topic
-
Nature Communications

An open access, multidisciplinary journal dedicated to publishing high-quality research in all areas of the biological, health, physical, chemical and Earth sciences.
Related Collections
With Collections, you can get published faster and increase your visibility.
Women's Health
Publishing Model: Hybrid
Deadline: Ongoing
Advances in neurodegenerative diseases
Publishing Model: Hybrid
Deadline: Dec 24, 2025




Please sign in or register for FREE
If you are a registered user on Research Communities by Springer Nature, please sign in