AI-Descartes: Combining Data and Theory for Derivable Scientific Discovery
Published in Protocols & Methods
A new point of view for Scientific discovery
In our work, we are merging a first-principles approach, which has been used by scientists for centuries to derive new formulas from existing background theories, with a data-driven approach that is more common in the machine learning era. This combination allows us to take advantage of both approaches and create more accurate and meaningful models for a wide range of applications. By incorporating both first-principles and data-driven insights, we can achieve a deeper understanding of the underlying processes and phenomena, and more effectively capture the complexity of real-world systems.
Comparison with the state-of-the-art
One key difference between our approach and other existing methods is our development of a novel approach for symbolic regression that allows for the creation of larger and better formulas. However, the most innovative aspect of our work is the introduction of a reasoning module that sets us apart from existing methods.
While other methods may use simple constraints (e.g., a formula must be always positive) to discover formulae, our reasoning module considers axioms from a background theory that describes the environment under study. This background theory includes variables not present in the data and provides more information about the environment than just the specific phenomenon being studied. By using a background theory, we can refine and distinguish the formulas generated by our symbolic regression module.
Other systems based on symbolic regression (such as Eureqa, PySR, AI Feynman, and Bayesian Machine Scientist) output multiple solutions that approximate the data with varying degrees of accuracy. However, these solutions may overfit or underfit the data, and it can be difficult to distinguish the best formula from the pool of hypotheses. Our reasoning module uses logical reasoning to identify the best solution, whether it is the formula that can be logically derived from the background theory or the one that is the closest to the derivable ground truth law. Furthermore, our reasoning module can be integrated with other symbolic regression modules as well.
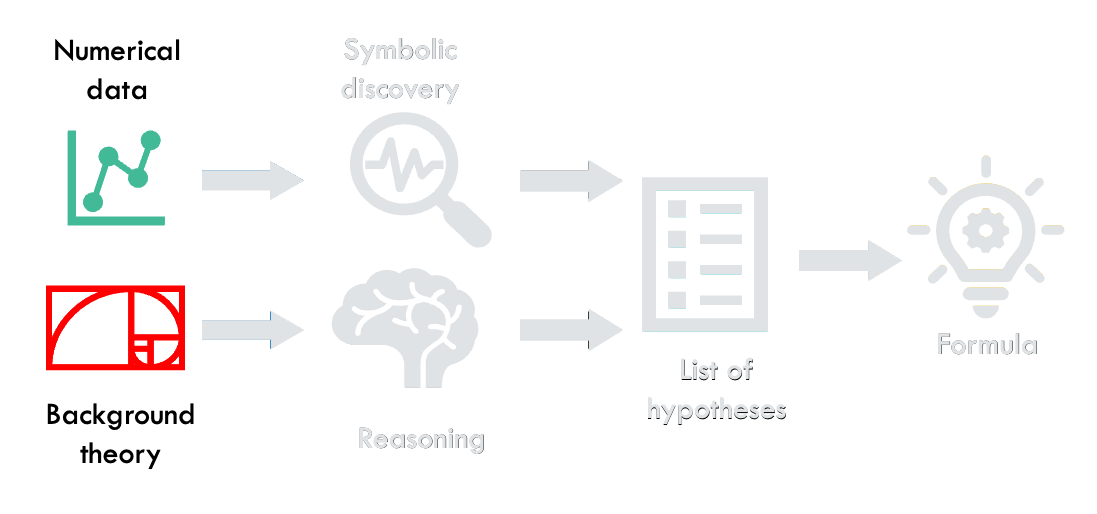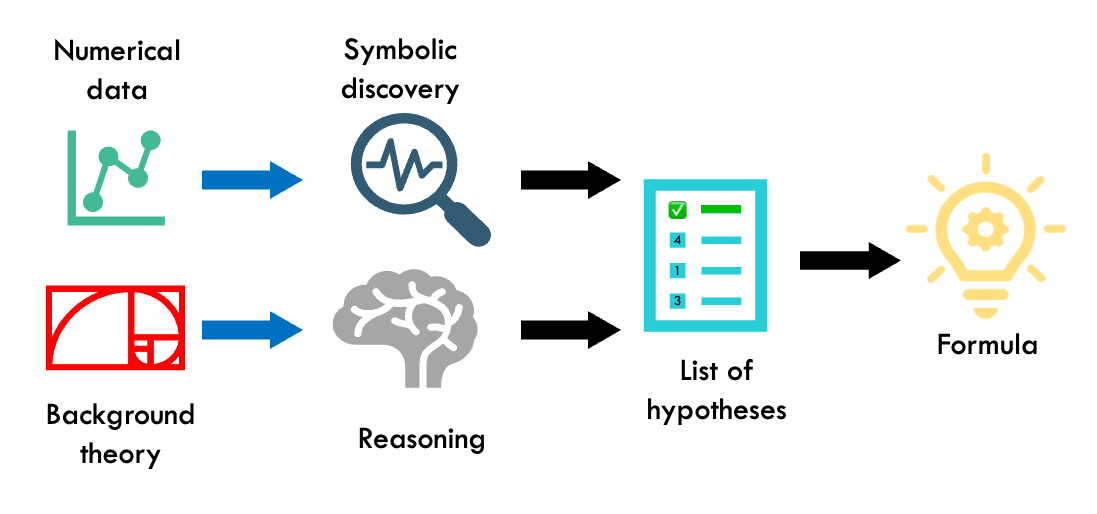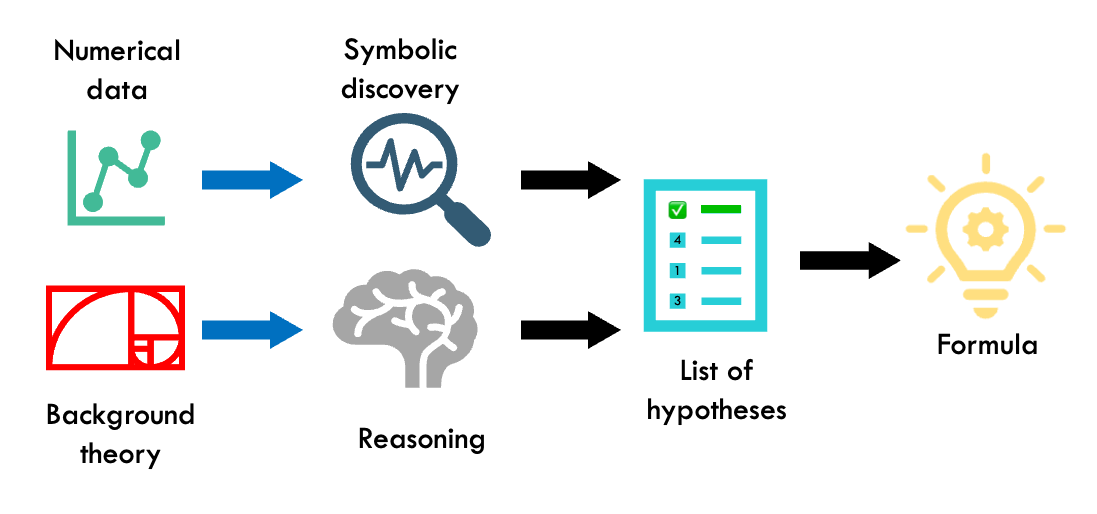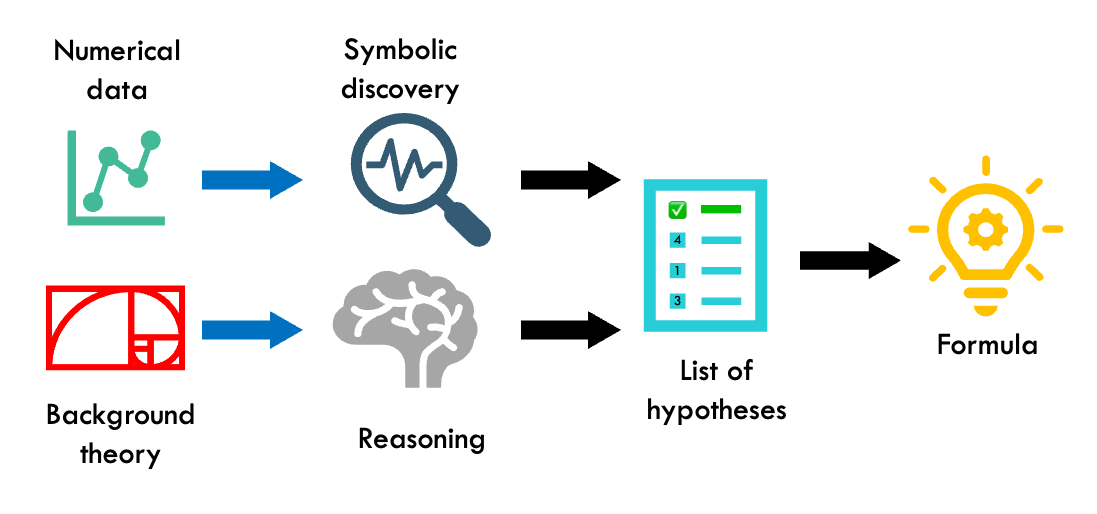
Our focus: real-world datasets
Our approach is particularly well-suited for analyzing a specific type of scientific data, namely data from experimental measurements, and small datasets. Real data presents a challenge in that it is often very noisy, which can lead to a proliferation of overfitting formulas that are unable to distinguish between noise and true signal. However, our reasoning method allows us to identify the best solution from the pool of potential solutions, even in the presence of noisy data.
Similarly, small datasets can be a challenge for many machine learning tools that require a large amount of data to function effectively. However, our novel symbolic regression tool can provide highly accurate predictions with very few data points (e.g., less than 10).
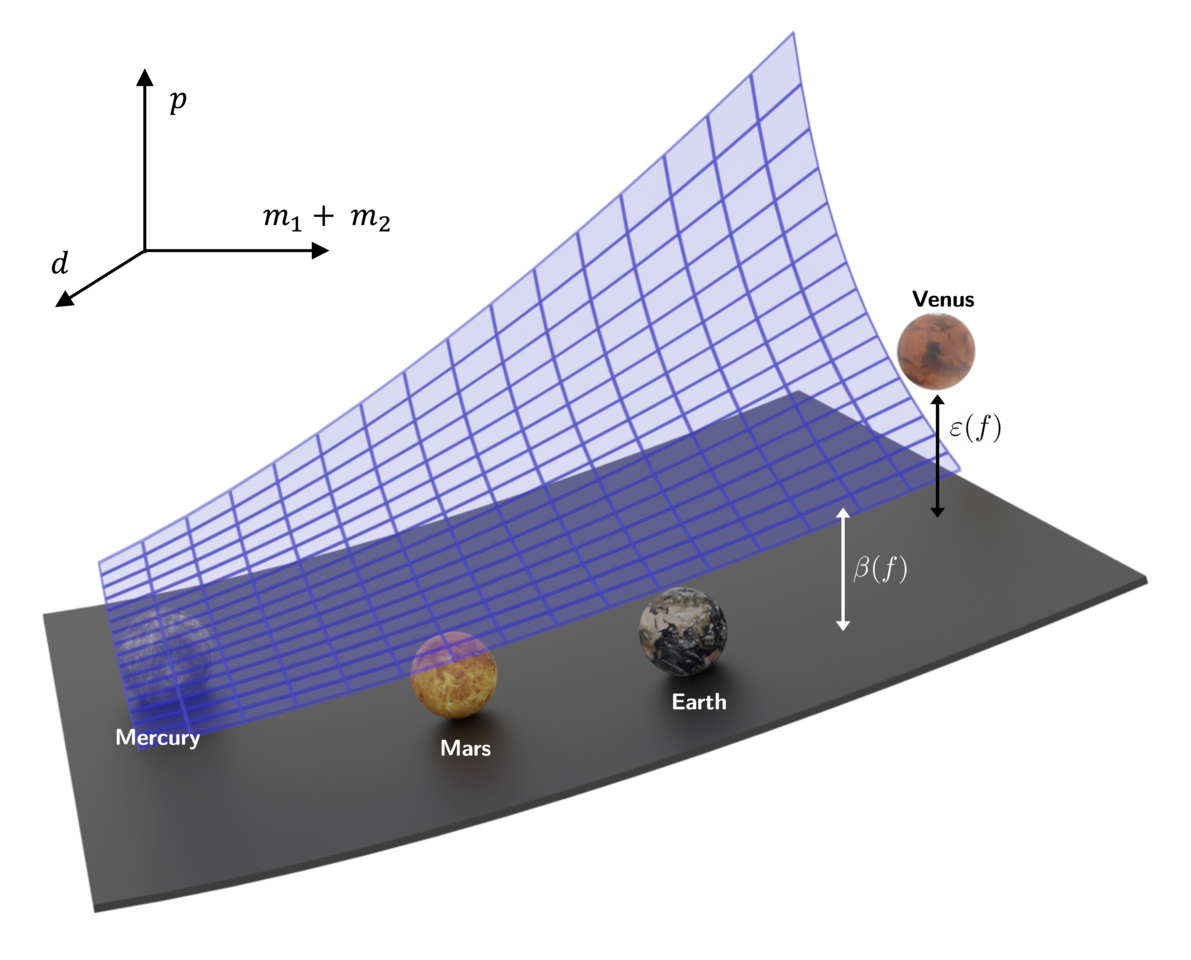
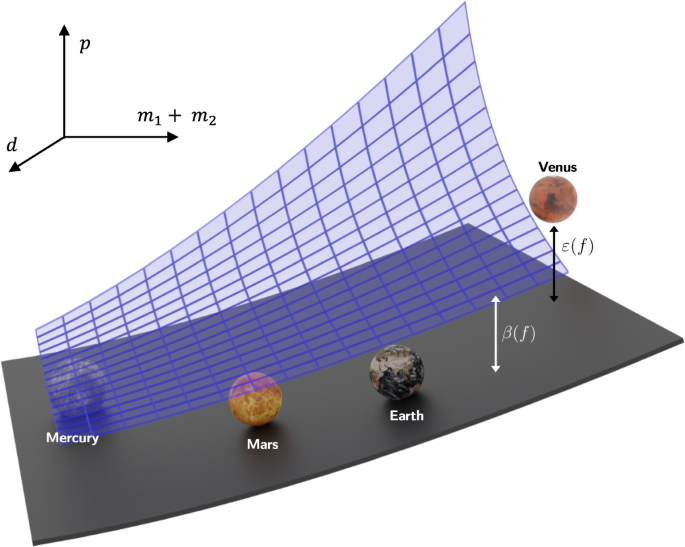
In our work we demonstrated the capability of our model on three real-world problems: Kepler’s third law of planetary motion, Einstein’s relativistic time-dilation law, and Langmuir’s theory of adsorption.
What we envision for the future
A key area of focus for our future research will be to identify and create new datasets that contain both real measurement data and an associated background theory. Currently, many datasets available for analysis are based on simulations, which can limit their applicability to real-world scenarios. In fact, many machine learning algorithms that work well on simulated data can perform poorly when faced with real-world data, which is often noisier and more irregular. Moreover, most of the datasets currently available for analysis lack any associated background theory. This can create a significant disconnection from the underlying principles and known scientific laws that could be crucial for making new discoveries and advancing our understanding of the world.
In addition to this, our group is continuing to explore other aspects of this research area. One line of inquiry is to focus on a deeper integration of background theory and data in the case of restricted families of equation types. Another area of focus is the logical axiomatization of chemistry, which could have important implications for the field. Lastly, we are working on the imposition of constraints, of which scientific background theories are an example, to neural models.
Take-away message
One of the most exciting aspects of our work is the potential to make significant advances in scientific research by integrating data-driven approaches with the first-principles approach used by classical scientists. By leveraging both approaches simultaneously, AI-Descartes has the potential to discover new scientific laws that were previously unknown.
It's interesting to note that with our method, we were able to rediscover Langmuir’s adsorption equation, which was awarded the Nobel Prize in Chemistry in 1932. While we may be just a few years too late in terms of original discovery, this serves as a powerful demonstration of the potential of our approach to uncover important scientific principles and laws.
Follow the Topic
-
Nature Communications

An open access, multidisciplinary journal dedicated to publishing high-quality research in all areas of the biological, health, physical, chemical and Earth sciences.
Related Collections
With Collections, you can get published faster and increase your visibility.
Women's Health
Publishing Model: Hybrid
Deadline: Ongoing
Advances in neurodegenerative diseases
Publishing Model: Hybrid
Deadline: Mar 24, 2026



Please sign in or register for FREE
If you are a registered user on Research Communities by Springer Nature, please sign in