For a long time, people have been pursing holographic technology that can provide large viewing angle, large depth, realistic and interactive 3D images. In traditional 3D holography, the phase and amplitude information of an object are dynamically regulated by a spatial light modulator or digital mirror device. The pixel size of these modulators is usually larger than 3.7 µm. Such large pixel size leads to narrow holographic viewing angle of around 8° limiting the application of 3D holography The emerging metasurface provides a unique opportunity for holography due to the sub-wavelength structures that can arbitrarily control the properties of light and realize a larger viewing angle. Although meta-holography provides sufficient viewing angle, the challenge of realizing large depth 3D imaging has not been overcome. 
In this work, we develop a 3D meta-holography based on angular spectrum diffraction theory to break through the depth limit. Figure 1 is the concept of the proposed 3D meta-holography. By developing the angular spectrum diffraction theory into meta-holography, the metasurface structure with independent polarization control is used to create a polarization multiplexing 3D meta-hologram. The fabricated amorphous silicon metasurface increases the depth range by 47.5 times and realizes 0.95 dm depth reconstruction for polarization independent and different color 3D meta-hologram in visible. Such polarization controlled large-depth color meta-holography is expected to open avenue for data storage, display, information security and virtual reality.

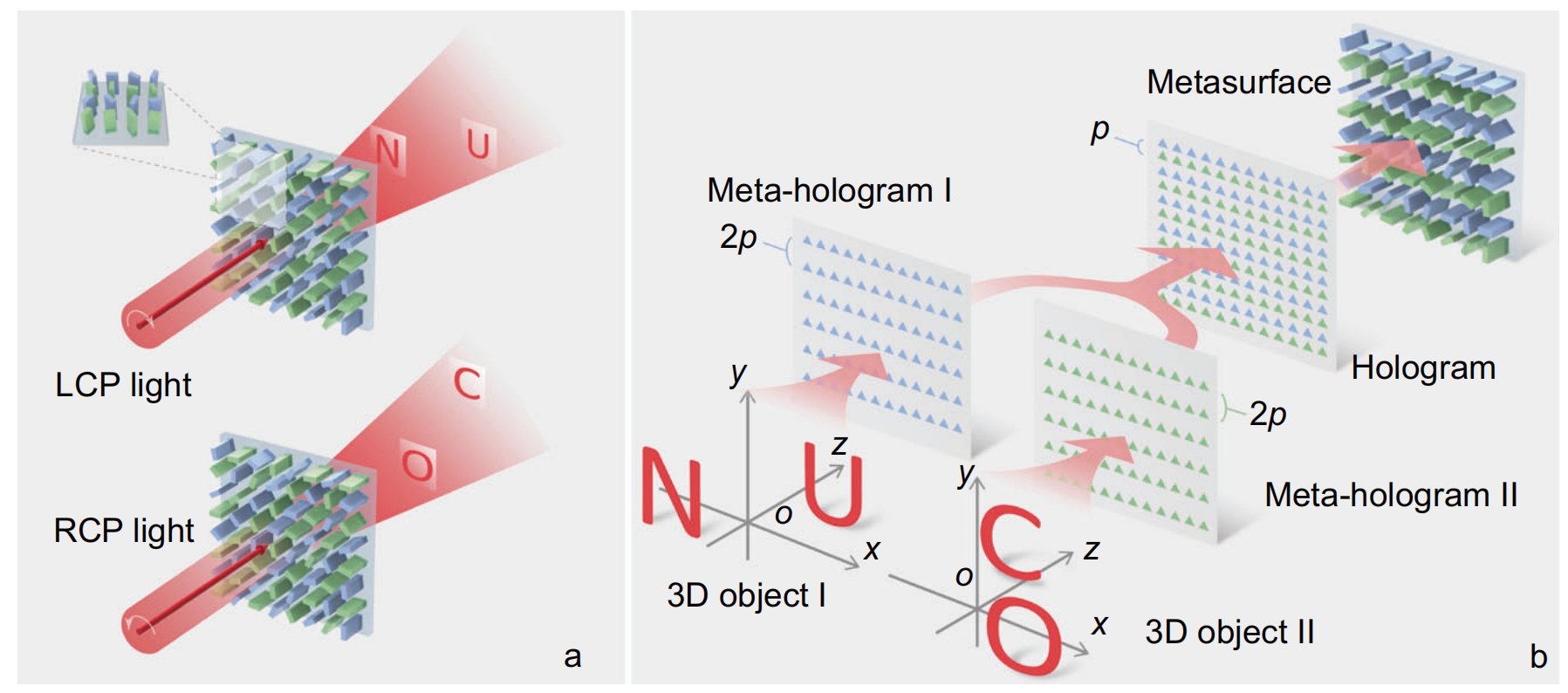
The designed metasurface is based on the principle of geometric phase control to realize the independent control of light field phase for each unit cell. The unit cell of the metasurface consists of a rectangular amorphous silicon nanorod fabricated on a quartz substrate. The Pancharatnams-Berry phase is utilized for a broadband non-dispersive phase control by rotating the principle axis of the birefringent nanorod. The relationship between the PB phase shift φ and rotation angle θ satisfies φ=±2θ, where the positive sign is taken when the polarization state of the incident light is LCP, and the negative sign is taken when the polarization state is RCP. The schematic illustration of the proposed metasurface for encoding the hologram and manipulating the corresponding polarization states simultaneously is shown in Fig. 1b. For two different 3D objects, the corresponding meta-holograms I and II are calculated based on the angular spectrum diffraction theory. The two meta-holograms correspond to the a pair of orthogonal circular polarization states, respectively. The pixel spacings are p and 2p along x and y directions, respectively. To reduce the interference between adjacent phases, we use line-by-line insertion to synthesize two sub-holograms into a final hologram, thus obtaining the complex amplitude modulation information corresponding to the metasurface. When LCP or RCP light irradiates the metasurface, holographic reconstruction of different 3D objects with large depth can be realized. This function is realized by the complex amplitude modulation of two orthogonal polarization bases provided by the metasurface, which is difficult to realize by using spatial light modulators in the traditional optical systems.
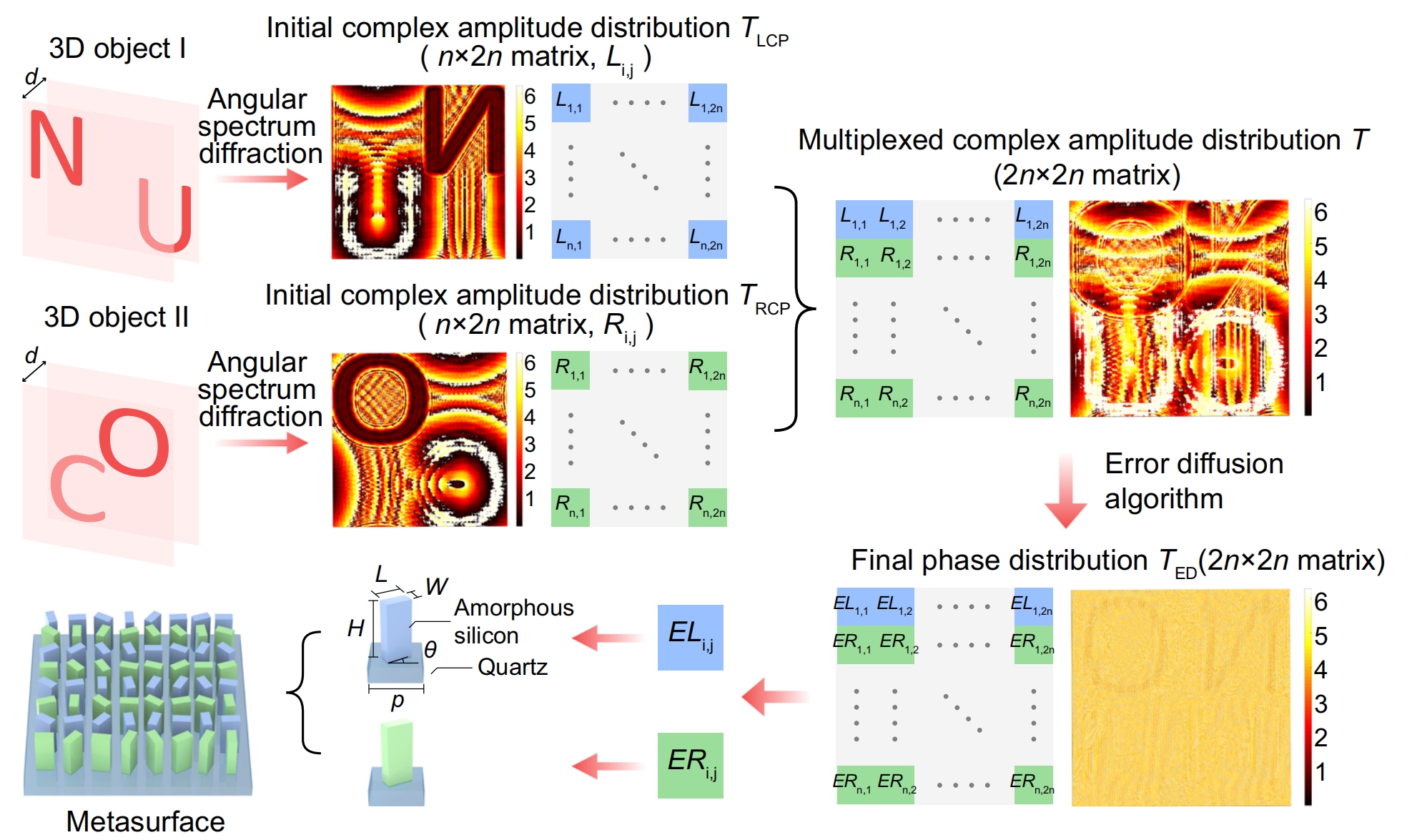
When calculating the hologram, all the light fields, spectra and transfer functions are discretely sampled with equal grids, as shown in Fig. 2. The under-sampling operation in the discrete sampling process causes errors, which will lead to spectrum aliasing, and finally the reconstructed light field of large depth holography will be seriously affected. To ensure that the high-frequency information of 3D objects is not affected by the spectrum aliasing in the process of meta-holography reconstruction, the transfer function need be restricted. After the initial complex amplitude distributions TLCP and TRCP are acquired by using the angular spectrum diffraction principle, they are horizontally interleaved to obtain the multiplexed complex amplitude distribution denoted as T. In the calculation of angular spectrum diffraction, both TLCP and TRCP are quantized into matrices of size (n×2n). Therefore, the matrix of synthesized T is (2n×2n). Because the designed metasurface is used to realize the phase modulation, if the amplitude information of the complex amplitude hologram is directly removed, each pixel will have an error, which will affect the quality of holographic reconstruction. In order to reduce this error, after obtaining the pure phase information, the pixel points are scanned one by one by using the error diffusion algorithm, and the error of each pixel point is diffused to the adjacent pixels that have not been scanned according to a certain weight. The final phase distribution TED is obtained by using iterative optimization, which leads to a significant improvement in the quality of holographic reconstruction.

Overall, we develop the angular spectrum diffraction theory into meta-holography, and design the metasurface structure with independent polarization control to realize color 3D meta-holography with large depth, high information capacity, and a polarization multiplexing capability. The proposed 3D meta-holography opens up new possibilities for naked-eye 3D display, volumetric data storage, encryption, medical imaging and virtual and augmented reality.