Learning local equivariant representations for large-scale atomistic dynamics
Published in Materials
Molecular dynamics simulations have become an indispensable tool for materials scientists, chemists, and biologists, providing detailed atomistic understanding of how molecules and materials behave over time. At the core of the simple process of iteratively integrating Newton's equations of motion lies however the requirement for a description of the potential energy surface of the system that is simultaneously accurate and highly computationally efficient. Over the past decades, significant effort across the computational sciences has been expended towards improving the prediction of energies and atomic forces. Traditionally, two avenues have been pursued: on one side is first-principles calculations, such as e.g. density functional theory (DFT) or coupled-cluster methods, which are able to provide a highly accurate quantum-mechanical description of the system. However, these methods scale poorly with system size and are thus limited to short time-scales and small systems. On the other side, classical interatomic potentials aim to describe the potential energy surface based on extremely simple functional forms. While these classical potentials can be scaled to massive systems and large time-scales, their form inherently limits their accuracy, potentially resulting in unfaithful dynamics.
Machine learning has over the past 15 years emerged as a promising approach to move past this dilemma: by learning to approximate the energies and forces of accurate reference calculations with a computationally more efficient, linear-scaling surrogate model, machine learning interatomic potentials aim to bypass this accuracy-efficiency trade-off. Fast progress has been made as new methods are proposed almost weekly, with modern deep learning approaches achieving remarkably high fidelity with respect to first-principles methods. This accuracy, however, has come at a cost: while potentials have become ever more accurate, modern deep learning interatomic potentials have also become increasingly compute-heavy, limiting in particular the time- and length-scales that can be studied with them.
Among current approaches, message passing interatomic potentials display by far the highest accuracies: the atomistic structure is first represented as a graph, in which nodes correspond to atoms in the molecule/material and an edge is drawn in the graph if two atoms are within some interatomic distance of one another. Over the different layers of the network, information is then propagated from node to node (or atom to atom), which iteratively communicates the node states to their neighbours, thereby correlating them, and converging to an improved description of the system at the final layer.
A particular class of message passing interatomic potentials that has recently enabled unprecedented levels of accuracy, sample efficiency, and robustness has been Equivariant Interatomic Potentials, starting from the leading NequIP framework [1]. While conventional, invariant interatomic potentials operate on invariant features of the geometry, such as interatomic distances or angles, equivariant potentials operate directly on the raw interatomic position vector, allowing a more faithful representation of the atomistic geometry.
The price to pay for the high accuracy of message passing interatomic potentials, however, is that they are currently limited to small systems, which has significantly limited realism as many interesting chemical processes require large numbers of atoms to be accurately represented. This limitation is inherently tied to the message passing paradigm, since iteratively propagating information along the atomistic graph simultaneously increases the effective cutoff of each node in the system. A simple, but illustrative example is water: under a local cutoff of 6 Angstrom, each atom in bulk water at a pressure of 1 bar and a temperature of 300K has 96 neighbours including the central atom. By iterating over six message passing layers, this effective cutoff grows to 36 Angstrom. Since the number of neighbouring atoms grows cubically with this interaction distance, each atom now has 20,834 atoms in its receptive field. In the message-passing paradigm, information from each of these neighbours flows into the current central node and has to be computed. This large receptive field makes it extremely difficult to leverage parallel computation, since each device would require access to the node states of all >20,000 nodes within the receptive field.
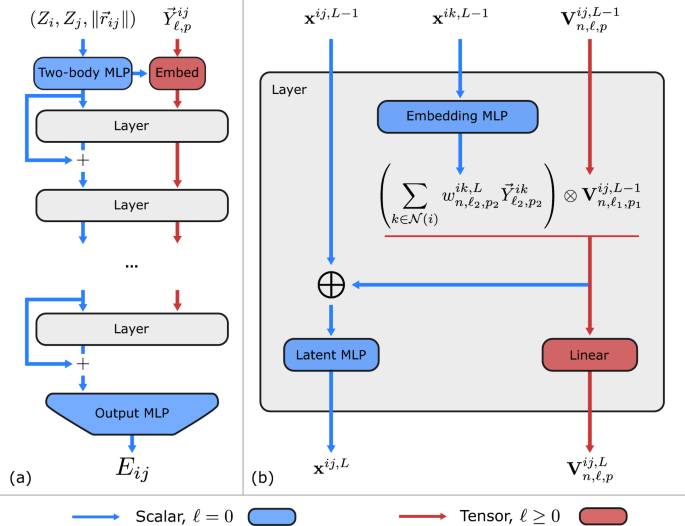
In the present work, we developed Allegro, a deep learning approach that moves past this severe limitation by keeping all interactions strictly local to the neighbourhood of the central atom, while retaining the key equivariant nature of the interatomic potential. This locality allows Allegro to distribute work across devices, leading to a previously impossible combination of accuracy and scalability. The key idea of the Allegro architecture is to describe the potential energy of a system as a sum over per-pair energies. Each pair of atoms (i, j) - central to atom i and describing the state of a pair of atoms i and j - is then featurised as a latent vector in the neural network. Over the different layers of the network, this latent representation is iteratively refined and coupled to information from other neighbours of atom i. This coupling increases the many-body correlation among particles, leading to increasingly high-fidelity descriptions of the potential energy surface. In contrast to message passing interatomic potentials, the coupling in Allegro is no longer tied to a simultaneous increase in the receptive field. Instead, interactions are kept strictly local w.r.t. to the current central atom i and no information from outside the local cutoff sphere of i ever enters the environment. This locality allows the receptive field to remain small and makes the method massively parallelizable. An overview of the Allegro architecture can be sen in the below figure.
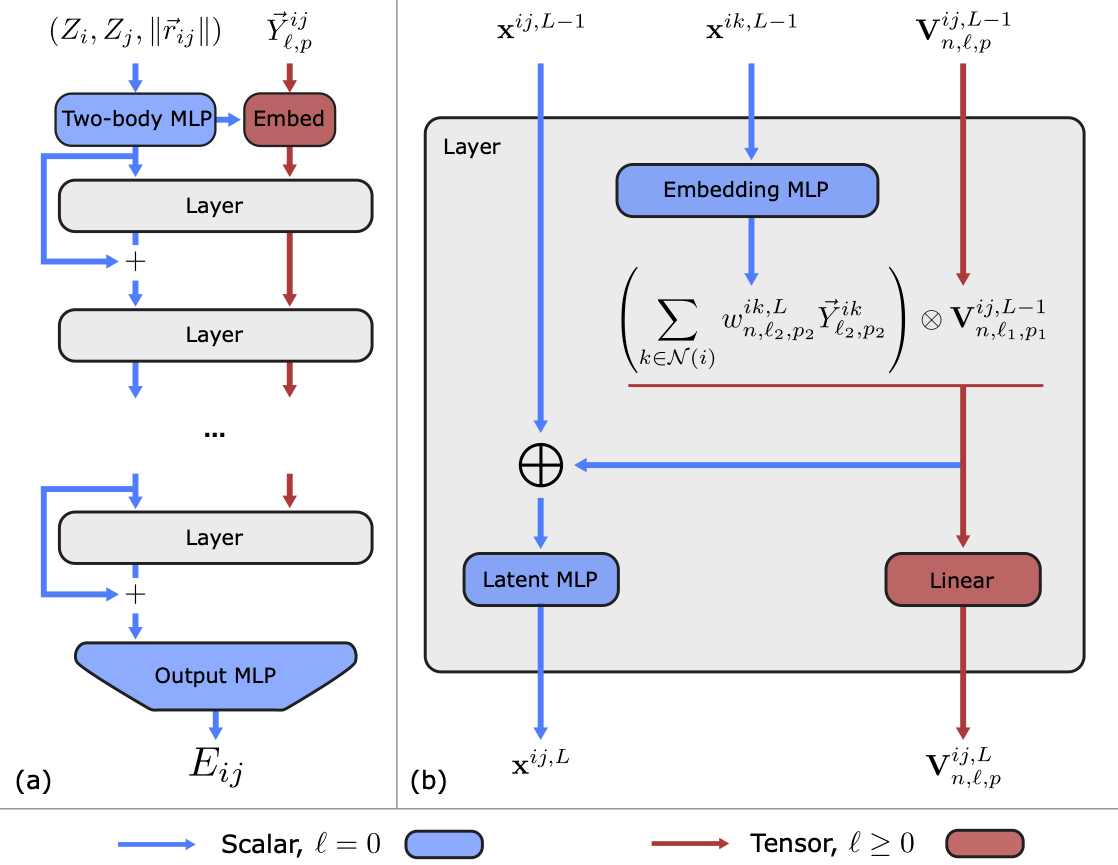
The efficacy of Allegro in the present work is tested on a large and diverse set of small molecules and materials. We first measured the ability of the machine learning system to accurately model small molecules on the revMD-17 and QM9 benchmarks and demonstrate state-of-the-art accuracy. As a next step, we probed the robustness of Allegro: in practice, while machine learning potentials are typically trained on data sampled from one distribution, they are then deployed and may over the course of a long simulation encounter entirely new structures that are different from what it was trained on. Therefore, in addition to the requirement to perform well on data sampled from a similar distribution as the potential was trained on, it is also of high interest for machine learning interatomic potentials to be transferable to out-of-distribution data. We test this by assessing the performance of the Allegro potential by training it on data sampled at a low temperature of T=300K and then measuring its performance at increased temperature of T=600K and T=1,200K. We find that the local Allegro potential demonstrates remarkably high transferability, despite being only trained on low-temperature configurations. Finally, we validate the performance of the potential on a complex lithium phosphate electrolyte, Li3PO4, and demonstrate that Allegro can accurately predict the structure of the amorphous phase of the system as well as the Li-ion dynamics.
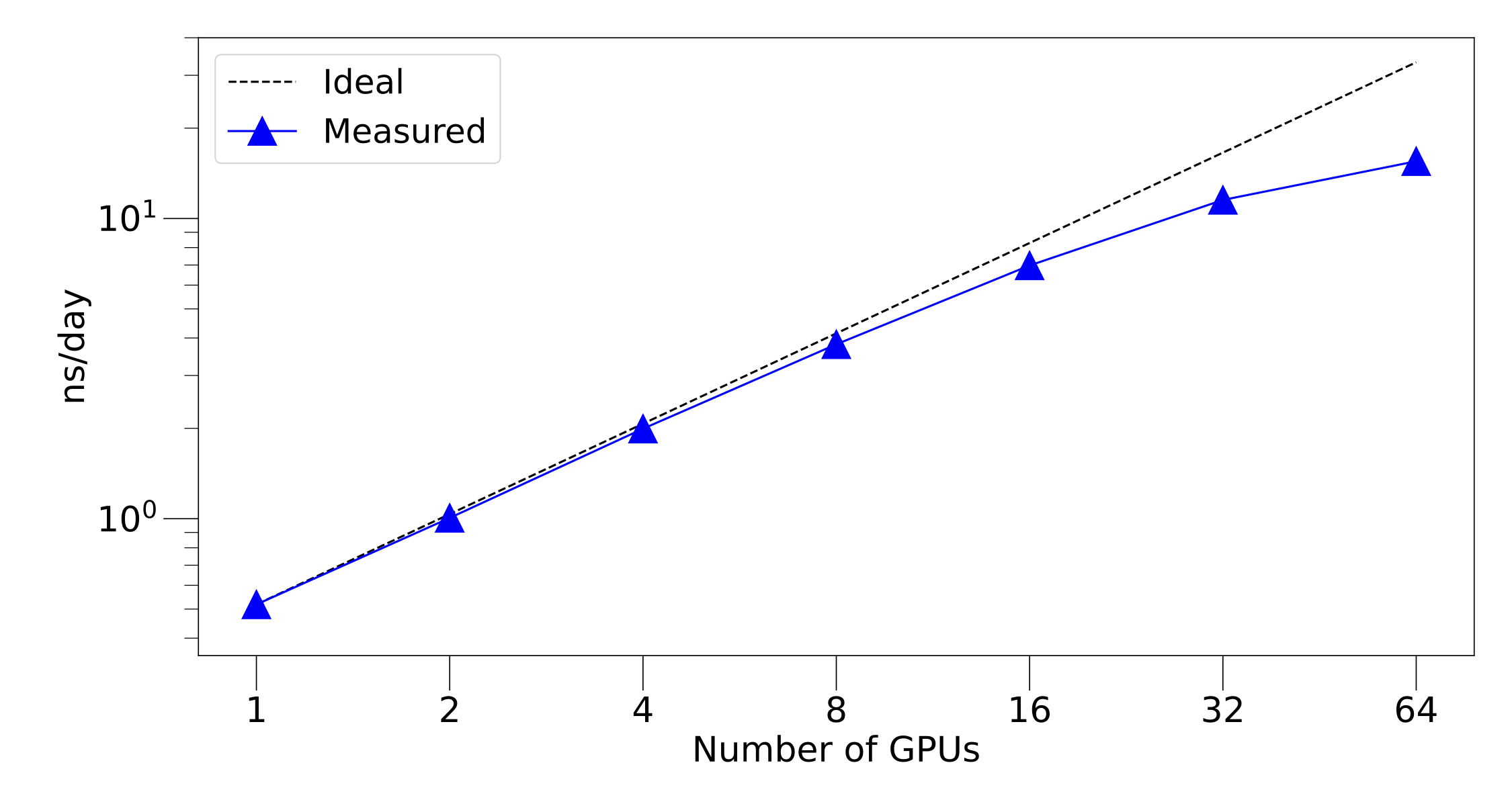
Having demonstrated that Allegro retains the high accuracy and transferability of the NequIP equivariant message passing interatomic potential, we show how the locality of the approach allows us to scale to large systems and longer time-scale. We perform this test on a large system of 421,824 atoms of the Li3PO4 system. In particular, we perform a strong scaling test, keeping the number of atoms of the system constant, but increasing the number of GPUs. The figure below shows how the computational efficiency - as measured by the accessible simulation speed measured in [ns/day] - changes with the number of GPUs we use (timings were performed in the molecular dynamics code LAMMPS). While on a single GPU the system is able to achieve approximately 0.5 ns/day, when increasing the compute, this number increases to approximately 16 ns/day when using 64 GPUs. We note that such an increase would be currently impossible with message passing approaches since they could not easily leverage the additional compute.
Finally, we also demonstrate that with Allegro we can scale to truly massive systems, greatly increasing the realism of our simulations. To this end, we simultaneously increase the number of atoms as we increase compute. When scaling from 1 GPU to 128 GPUs, this finally allows us to run a molecular dynamics simulation of more than 100,000,000 atoms of a bulk silver system. Remarkably, this is achieved while retaining a high through-put of >1.5 ns/day. As a point of comparison, the 2020 ACM Gordon Bell Prize was award to the Deep Potential Molecular Dynamics system (also a machine learning interatomic potential) for achieving a 100-million-atom simulation on more than 27,000 GPUs. Here we are able to achieve a simulation of similar size on as few as 128 GPUs.
We believe the Allegro approach provides a significant step forward in pushing the boundary of accuracy and computational efficiency of machine learning interatomic potentials, leading to increased realism and predictive power of molecular simulations. The method is publicly available on Github under a MIT license, has a GPU-enabled integration with the popular molecular dynamics simulation code LAMMPS, comes with extensive tutorials for new users, is actively being supported and developed by the authors, and is already being used by scientists all around the globe to study complex molecular and materials systems.
Paper: nature.com/articles/s41467-023-36329-y
[1] Batzner et al. (2022). E (3)-equivariant graph neural networks for data-efficient and accurate interatomic potentials. Nature communications, 13(1), 2453.
[2] Musaelian, A., Batzner, S., Johansson, A. et al. Learning local equivariant representations for large-scale atomistic dynamics. Nat Commun 14, 579 (2023).
Follow the Topic
-
Nature Communications

An open access, multidisciplinary journal dedicated to publishing high-quality research in all areas of the biological, health, physical, chemical and Earth sciences.
Related Collections
With Collections, you can get published faster and increase your visibility.
Clinical trials 2025
Publishing Model: Open Access
Deadline: Dec 31, 2025
Women's Health
Publishing Model: Hybrid
Deadline: Ongoing


Please sign in or register for FREE
If you are a registered user on Research Communities by Springer Nature, please sign in